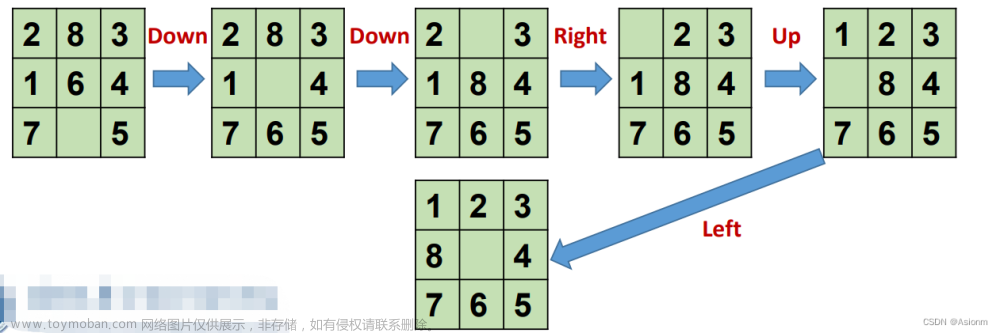
本关任务:编写代码实现广度优先搜索一个给定的树。
相关知识
为了完成本关任务,你需要掌握广度优先搜索算法的原理与实现。
广度优先搜索步骤
广度优先搜索一般是采用先进先出( FIFO )的队列来实现的,在这里我们用到了两个表:
-
Open :是一个先进先出的队列,存放称为端结点的待扩展结点。
-
Closed :是一个表,存放被扩展过的结点。
广度优先搜索实现
下面是广度优先搜索的伪码:
Procedure breadth_first_searchbeginopen:=[start];closed:=[] *初始化while open≠[]dobegin从 open 表中删除第一个状态,称之为 n ;将 n 放入 closed 表中;if n =目的状态 then return ( success );生成 n 的所有子状态;从 n 的子状态中删除已在 open 表或 closed 表中出现的状态; *避免循环搜索将 n 的其余子状态,按生成的次序加入到 open 表的后段;end;end;
编程要求
根据提示补全右侧编辑器 Begin-End 区间的代码,输出根据广度优先遍历后的节点次序。
测试说明
平台会对你编写的代码进行测试:
测试输入:
{'mazz':{'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'F': ['G', 'H'],'D': [],'E': [],'G': [],'H': []},'start':'A','end':'D'}
预期输出:
ABCD
开始你的任务吧,祝你成功!
答案
def PlayMazz(mazz, start, end):
'''
走迷宫,从start走到end
:param mazz: 图
:param start: 图的起点
:param end: 图的出口
'''
# queue为队列,当队列为空或者当前地点为终点时搜索结束
queue =list()
closed=set()
queue.append(start)
#********* Begin *********#
while(queue!=0):
closed.add(queue[0])
if queue[0]==end:
print(end,end='')
break
else:
print(queue[0],end='')
for i in mazz[queue[0]]:
if i in closed:
pass
else:
queue.append( i )
queue.remove(queue[0])
#********* End *********#第二关
第2关:深度优先搜索
任务描述
本关任务:编写代码实现深度优先搜索来遍历整棵树。
相关知识
为了完成本关任务,你需要掌握深度优先搜索算法的原理与实现。
深度优先搜索概述
深度优先搜索( DFS ),顾名思义,就是试图尽可能地深入树中。每当搜索方法可以做出选择时,它选择最左(或最右)的分支(尽管它通常选择最左分支)。如图1所示的树是 DFS 的一个例子:
图1 深度优先搜索
图中树先沿着1,2,3进行扩展,在节点3无后继节点可产生,就回溯到节点1沿着4继续扩展,并产生新的节点5和6,若6还不是目标节点,则回溯到4继续扩展,以此类推,直到找到问题的解方可结束,从中方可体会“深度”的含义。
为了描述图中节点的深度,给出树的节点的深度定义如下:
-
根结点的深度是0;
-
除根节点外,其他节点的深度是其父结点的深度加1。
例如图1,1是树根结点,所以深度为1,2结点的深度是它的父亲结点,也就是1结点的深度加1为2。
深度优先搜索步骤
深度优先搜索一般是采用后进先出( LIFO )的队列来实现的,在这里我们用到了两个表:
-
Open :存放称为端结点的待扩展结点。
-
Closed :存放被扩展过的结点。
如图2是深度优先搜索算法流程图:
图2 深度优先搜索算法流程图
所谓后继结点是否为目标结点,也就是该结点的子结点是否为我们所求的解。
下面给出图1深度优先搜索的过程:
Open=[1] Closed=[]
图3
Open=[2,4,8] Closed=[1]
图4
Open=[3,4,8] Closed=[2,1]
图5
Open=[4,8] Closed=[3,2,1]
图6
Open=[5,7,8] Closed=[4,3,2,1]
图7
Open=[6,7,8] Closed=[5,4,3,2,1]
图8
Open=[7,8] Closed=[6,5,4,3,2,1]
图9
Open=[8] Closed=[7,6,5,4,3,2,1]
图10
Open=[9] Closed=[8,7,6,5,4,3,2,1]
图11
Open=[] Closed=[9,8,7,6,5,4,3,2,1]
图12
深度优先搜索实现
Procedure depth_first_searchbeginopen:=[];closed:=[]while open≠[] dobegin从 open 表中方删除第一个状态,称之为 n ;将 n 放入 closed 表中;if n =目标状态 then return (success);生成 n 的所有子状态;从 n 的子状态中删除已在 open 或 closed 表中出现的状态;将 n 的其余子状态,按生成的次序加到 open 表的前端;end;end;
与广度度优先搜索使用 FIFO 队列不同,深度优先搜索使用 LIFO, Last In First Out 的队列结构,即最新生成的结点最早被选择扩展。因此,为了实现方便,深度优先搜索算法一般抛弃 LIFO 队列而采用递归式结构实现。
深度受限搜索
在无限状态空间里,深度优先搜索可能会陷入无解的分支里跳不出来。深度受限搜索 Depth-Limited-Search 通过设置一个深度界限l来避免此问题,即深度为l的结点被当做为没有后继的叶子结点。 虽然深度界限解决了无穷路径的问题,但是该算法是不完备的。假设正确解在深度为d的结点,若设置的l小于d,则目标结点的深度超过了深度限制,那么该算法无法得到目标解;若设置的l大于d,由于会增加很多无用的搜索空间,深度受限搜索则不是最优的。深度优先搜索可以看作是特殊的深度受限搜索,其受限深度l=∞。
Procedure depth_limited_searchbeginopen:=[];closed:=[];d:=深度限度值while open≠[] dobegin从 open 表中方删除第一个状态,称之为 n ;将 n 放入 closed 表中;if n =目标状态 then return (success);if n的深度<d then continue;生成 n 的所有子状态;将 n 的子状态中删除已在 open 或 closed 表中出现的状态;将 n 的其余子状态,按生成的次序加到 open 表的前端;end;end;
迭代加深的深度优先搜索
迭代加深的深度优先搜索 Iterative-Deepening-Search 结合了深度受限搜索,它不断的增大深度限制,首先是l=0,接着为1,然后为2,以此类推,直到找到目标解,即当深度界限达到d时,最浅的目标结点被找到。迭代加深的深度优先搜索结合了深度优先搜索和宽度优先搜索的优点。
Procedure iterative_deeping_searchbeginopen:=[];closed:=[];d:=深度限度值;a:=每次增加的搜索深度的跨度while open≠[] do调用depth_limited_searchd=d+aend;
编程要求
根据提示,补全右侧编辑器中 Begin-End 区间中 PlayMazz 函数中的代码,来实现对整棵树的深度优先搜索。
测试说明
平台会对你编写的代码进行测试:
测试输入:
{'mazz':{'A':['B','E'],'B':['C','D'],'C':[],'D':[],'E':[]},'start':'A','end':'E'}
预期输出:
ABCDE
开始你的任务吧,祝你成功!
答案
def PlayMazz(graph, start,end, visited=None):
'''
深度优先搜索,从1走到9
:param graph: 搜索的空间
:param start: 开始搜索的起点
:param visited: 已经搜索过的点集合
'''
if visited is None:
visited = set()
visited.add(start)
print(start, end='')
# 当前地点为终点时结束搜索
if start == end:
return
else:
for i in graph[start]:
PlayMazz(graph,i,end)
#********* Begin *********#
# 看看当前位置有哪些路可以走,如果能走并且之前没有走过就走
#********* End *********#
第3关:盲目搜索算法的应用





答案:
class Solution:
def __init__(self, n=0):
self.vis = [0]*n # 用于标记是否存在皇后的二维列表(初始值全为0)
self.ans = 0 # 用于存储答案(N皇后方案数,初始值0)
self.n = n # 用于存储皇后数量n
def solveNQueens(self):
"""求解N皇后问题(调用self.DFS函数)
:rtype: self.ans: int #返回N皇后放置方案数
"""
# 请在这里补充代码,完成本关任务
# ********** Begin **********#
self.DFS(0,self.n)
return self.ans
# ********** End **********#
def DFS(self, row, n):
"""深度优先搜索N皇后问题的解空间
:type: row: int #NxN棋盘的第row行
:type: n: int #皇后数量n
:rtype: None #无返回值
"""
# 请在这里补充代码,完成本关任务
# ********** Begin **********#
if row == n:
self.ans += 1
return
while self.vis[row] < n:
# print(1)
if self.judge(row):
self.DFS(row + 1, self.n)
self.vis[row] += 1
else:
self.vis[row] += 1
if self.vis[row] == n:
self.vis[row] = 0
return
# ********** End **********#
def judge(self,row): # 判断是否在同一列、同一对角线上
if row == 0:
return True
for i in range(row):
if abs(self.vis[row] - self.vis[i]) == row - i or self.vis[row] == self.vis[i]: # 若在对角线上则两个皇后横轴和纵轴的距离相等
return False
return True
文章来源地址https://www.toymoban.com/news/detail-800628.html
文章来源:https://www.toymoban.com/news/detail-800628.html
到了这里,关于人工智能头歌实验(盲目搜索)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!