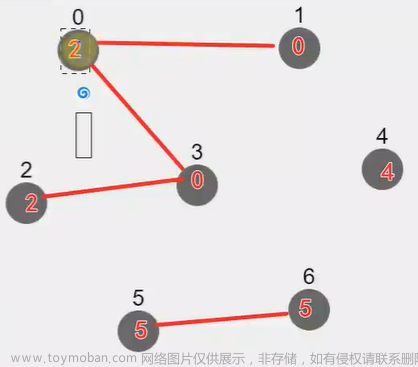
我们先来看太戈编程467题 攀亲戚
题目描述:
最近你发现自己和古代一个皇帝长得很像:都有两个鼻子一个眼睛,你想知道这皇帝是不是你的远方亲戚,你是不是皇亲国戚。目前你能掌握的信息有m条,关于n个人:第i条信息包含两个人的编号ai,bi,表示ai和bi是亲戚。你的编号是0,皇帝的编号是1,最大编号为n-1,请问能否通过信息推理出你和皇帝是不是亲戚? 备注:众所周知,亲戚关系具有传递性。
连通块问题三大杀手:1.DFS 2.BFS 3.并查集
我们先定义一个id[]数组,表示i号节点的老爸(不是祖宗)。那么……想象一下,把样例构建成一幅图,怎么做呢(想象着想象着就睡着了)?哈哈,我们将无向边化作有向边即可,什么意思呢,就是呢,这个,啊这,嗯,差不多。回到题目,我们发现,皇帝有两个鼻子一个眼睛。
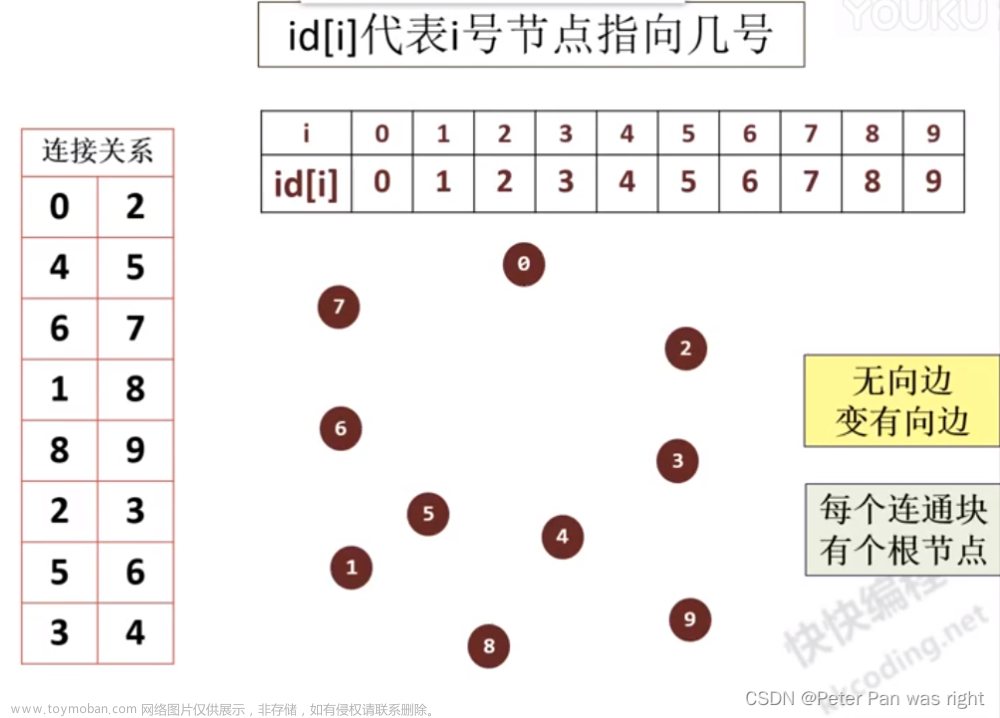
从这个变成……

按连接关系写完id[]。 即看到一条,就在图上加一条边。
那如何判断7和8是否连通呢?其实,我们用root()函数表示一个节点的祖宗,判断root(7)==root(8)就行了。
我们人手动加一条边好弄啊,但是计算机不认识啊,咋办嘞。

我们能不能直接7到8连条线呢?那这时我们发现8的老爸有两个耶,id[8]只能存一个。简单来说就是,不能去修改已经有父亲的点的id。那能不能让1认7做它父亲捏?1又没有父亲。可以是可以,但是……你想想找8的祖宗得走多远呢,换句话说,这棵树的深度太高。正确答案是让1认0做它老爸。所以,unite()函数要调用两次root()。

所以说main()函数如下
int main(){
cin>>m>>n;
for(ll i=0;i<n;i++) id[i]=i;
while(m--){
cin>>x>>y;
unite(x,y);
}
if(root(1)==root(0)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}root()和unite()如下
ll root(ll x){
if(id[x]==x) return x;
else return root(id[x]);
}
void unite(ll x,ll y){
ll rx=root(x),ry=root(y);
id(rx)=ry;
}此时看到代码的你立马复制黏贴。殊不知,没有AC。为什么呢?原来可以优化。

这叫“路径压缩”。那优化完的代码长什么样呢?
ll root(ll x){
return id[x]==x?x:id[x]=root(id[x]);
}就这一处变化。那有的小彭友说我用BFS、DFS那不香吗?为什么我们用并查集,因为unite()、root()函数时间复杂度为O(1)!总复杂度O(m+n)!总空间复杂度O(n)!文章来源:https://www.toymoban.com/news/detail-800822.html
并查集可视化网址:并查集 (Union-Find Disjoint Sets, 简称UFDS) - VisuAlgo文章来源地址https://www.toymoban.com/news/detail-800822.html
到了这里,关于Peter算法小课堂—并查集的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!