目录
1.原码的加减运算
(1)原码的加/减法运算
(2)溢出判断
(3)符号扩展
2.加法器原理
3.加法器实现补码的加减运算
1.原码的加减运算
(1)原码的加/减法运算
正+正--->绝对值做加法,结果为正
负+负--->绝对值做加法,结果为负
正+负--->绝对值大的减绝对值小的,符号同绝对值大的数负+正--->绝对值大的减绝对值小的,符号同绝对值大的数
原码的减法运算,只需要将“减数”符号取反,就可以转变为加法运算
对于正+正,负+负的情况,结果可能会溢出,例如:
A=15,B=-24,C=124:
[A+C]补=0,0001111+0,1111100=1,0001011 真值-117,A+C=15+124,不是-117,这就发生了溢出,8位补码的范围是-128~127
[B-C]补=1,1101000+1,0000100=0,1101100 真值+108,同样溢出,-24-124(两个负数相加得到正数)
对于补码加减不会的可以看看:http://t.csdnimg.cn/4oTZI
(2)溢出判断

只有“正数+正数”才会上溢---正+正=负
只有“负数+负数”才会下溢---负+负=正
例如:2+2,可以理解为2向右再移动两格,那么就到了-4

计算机判断溢出有3种方式:
1.采用一位符号位,设A的符号为(被加数正负号),B的号为(加数的正负号),运算结果的符号为(运算结果的正负号),则溢出逻辑表达式为
若V=0,表示无溢出;
若V=1,表示有溢出。
也就是:
:如果正(1)+正(1)=负(0)
:如果负(0)+负(0)=正(1)
都表示溢出
例如
[A+C]补=0,0001111+0,1111100=1,0001011
被加数符号为0,加数符号为1,运算结果的符号1,得到V=1,表示有溢出
2.采用一位符号位,根据数据位进位情况判断溢出符号位的进位Cs,最高数值位的进位C1
若符号位进位Cs=0,C1=1,表示发生上溢
若符号位进位Cs=1,C1=0,表示发生下溢
即Cs与C1不同时有溢出,所以可以用异或表示:Cs C1=1表示不同,=0表示相同
Cs与C1的含义如下图所示:

3.采用双符号位,正数符号为00,负数符号为11
[A+C]补=00,0001111+00,1111100 =01,0001011 上溢
[B-C]补=11,1101000+11,0000100 =10,1101100 下溢
记两个符号位为S1S2,则V=S1S2,若V=0,表示无溢出;若V=1,表示有溢出。
第一个符号位表示正确的正负性,第二个符号位表示实际的符号结果
例如,01,0表示正确符号位应该为正,实际却得到了1(负数),发生上溢
实际存储时,只会存储1个符号位,再运算前会复制一个符号位,运算时两个符号位会同时参与运算。 所以采用双符号位并不会增加存储空间。
注:双符号位补码又称:模4补码,单符号位补码又称:模2补码
01,0001011,如果我们将,看作 . 即01.0001011,那么0()1().0001011
模4就是相当于将位权小于4的部分保留,将大于4的部分舍弃,模2同理
(3)符号扩展
对于正整数,由于原,反,补码都是一样的,所以

对于负整数:
反码:在原码的基础上数值位补1
补码:在原码中找到最右边的1,将其左边的数值位全部取反

对于正小数,原,反,补码的表示都一样

对于负小数:
反码:在原码的基础上后半部分补1
补码:在原码的基础上,找到最右边的1,左半部取反,右半部分不变

由于原码的加减运算用电路实现比较复杂,所以通常用补码进行加减运算
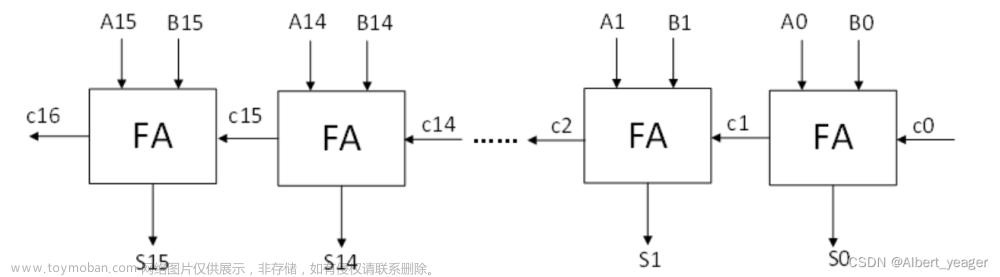
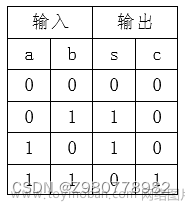
2.加法器原理
Cin表示来自低位的进位,Cout表示来自最高位的进位

A=1000,B=0111,Cin=0,那么算式就为
1 0 0 0
0 1 1 1
+ 0
----------
1 1 1 1
所以F=1111,因为最高位没有进位,所以Cout=0
A=1000,B=0111,Cin=1,那么算式就为
1 0 0 0
0 1 1 1
+ 1
----------1 0 0 0 0
所以F=0000,Cout=1
若想实现8bit加法器,那么可以将两个加法器串联起来,高位的Cin能接收来自地位的Cout
3.加法器实现补码的加减运算
首先看一下补码加减运算的方法:
补码X+Y:按位相加即可
补码X-Y:将补码Y全部按位取反,末位+1,得到[-Y]补,即X+[-Y]补,减法/变加法
这里可以这样理解,Y的最高位取反得到-Y,再将除最高位的其他位取反+1,得到[-Y]补
也就是将补码Y全部按位取反,末位+1
例如:
4bit补码,X=-8,Y=7,X补=1000,Y补=0111
对于4bit有符号的补码,有效范围是~= -8~7
X+Y=1111B
X-Y=1000+(1000+1)=
10001=1D,运算结果只保留低四位,最高位进位丢弃(发生溢出),此时的运算结果是错误的
4bit补码,X=3,Y=4。X补=0011, Y补=0100
X+Y=0111B=7D
X-Y=0011+(1011+1) = 1111B=-1D文章来源:https://www.toymoban.com/news/detail-800970.html
接下来看用加法器实现补码的加减运算:
Sub加/减控制信号:如果为加法则控制信号为0,如果为减法控制信号为1
当为加法时,控制信号为0,Cin=0,所以得到 X+Y+Cin=X+Y
当为减法时,控制信号为1,Cin=1,所以得到 X+Y+Ciin=X+(Y全部按位取反)+1

注:无符号整数的加/减法也可用该电路实现,且实现方法与有符号加减法一样,例如:
无符号数X=8,Y=7,用4bit表示,X=1000B,Y=0111B
X+Y=1111B=15D(十进制)
X-Y=1000+(1000+1)=
10001=1D,运算结果只保留低4位,最高位进位丢弃,这个结果是正确的
对比一下有符号数:4bit补码,X=-8,Y=7,X补=1000, Y补=0111
X+Y=1111B=-1D
X-Y=1000+(1000+1)=
10001=1D,这个运算结果是错误的
所以补码加减运算与无符号数加减运算都可以使用同一个电路使用,但是两者判断溢出的条件有所不同,这就需要标志位来区分
从下图可以看出,两个nbit的数相加,除了得到sum以外,还可以输出4个标志信息:OF,SF,ZF,CF

OF(Overflow Flag)溢出标志。溢出时为1,否则置0
注:OF只在有符号的加减运算中有意义,也就是说在无符号数的加/减运算中,即使OF=1,也不能说明发生了溢出
OF的计算方法:OF=最高位产生的进位次高位产生的进位
SF(Sign Flag) 符号标志。结果为负时置1,否则置0
计算方法:SF=最高位的本位和
SF同样只对有符号数有意义
ZF(Zero Flag)零标志,运算结果为0时ZF位置1,否则置0
ZF对有符号数,还是无符号数都是有意义的
CF(Carry Flag)进位/借位标志,进位/借位时置1,否则置0
CF=最高位产生的进位sub控制信号
只对无符号数有意义,对有符号数无意义

所以:对于有符号数的运算看OF,判断是否发生溢出,对于无符号数的运算看CF,判断是否发生溢出
再来看
无符号数 X=3,Y=4,用4bit表示,X=0011B,Y=0100B
X+Y=0111B=7D
X-Y=0011+(1011+1)=1111B=15D,显然3-4=15是错误的,无符号数无法表示负数-1
对比有符号数,运算结果是正确的:
4bit补码,X=3,Y=4。X补=0011B, Y补=0100B
X+Y=0111B=7D
X-Y=0011+(1011+1) = 1111B=-1D
所以我们可以看到,虽然同一电路得到的二进制结果相同,但是有符号数的运算结果与无符号数的运算结果是有所不同的。文章来源地址https://www.toymoban.com/news/detail-800970.html
到了这里,关于用加法器实现补码的加/减运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!