introduce
模态分析是研究结构动力特性的一种方法。模态是指机械结构的固有振动特性,一阶模态都对应特定的固有频率、阻尼比和振型。得到这些模态参数的过程就是模态分析。
- 如果是利用有限元计算获得,就称为计算模态分析;
- 如果是利用实验,采集信号的系统输入输出信号,进行参数识别后获得,就称为实验模态分析;
模态分析通常用来获得线性结构的一些振动特性:
- 固有频率
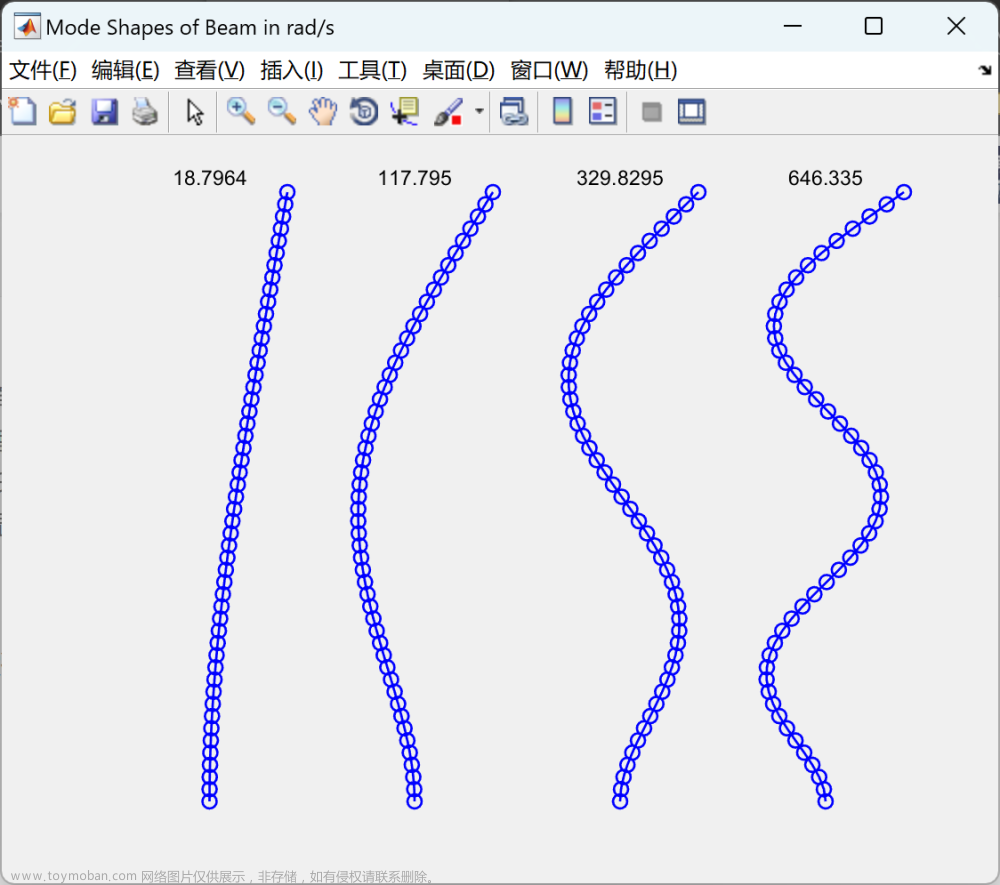
- 模态振型
- 振型的参与系数
- 有效质量
模态分析是所有结构动力学分析的基础,使结构避免发生共振。
模态分析的假设
- 结构没有外载荷(热,压力,温度,力等),即结构是自由震动的。
- 结构是线性的,其物理意义是,结构系统对任一组同时作用的激励的响应是该组内每一激励单独作用时系统的响应的线性叠加。(线性叠加原理)
- 时不变假设,即结构具有恒定的总体质量矩阵和总体刚度矩阵,并不随时间改变而改变。
总的来说就是,进行模态分析的时候,不用考虑大变形,接触问题,材料非线性。基本和静力学分析一致。
无阻尼模态分析理论
不考虑阻尼的自由振动,方程为:
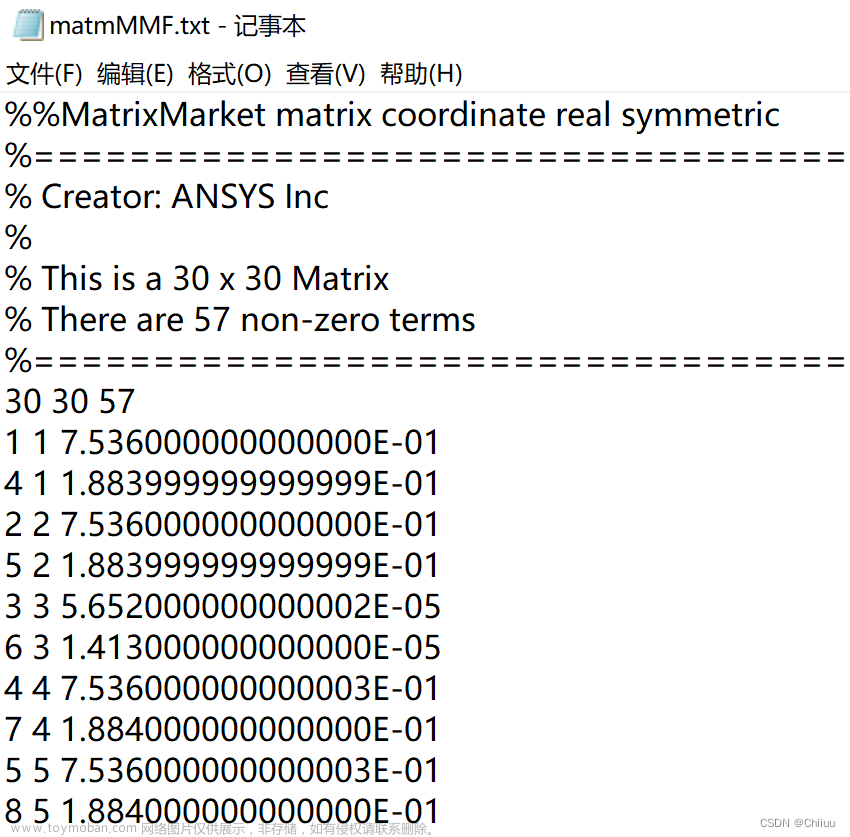
质量矩阵M由密度参数给定,刚度矩阵由材料本构关系,接触关系,约束情况等决定,即不考虑阻尼时,约束和材料确定后,结构的模态参数就确定了。

有阻尼模态分析理论

对于单自由度,含有阻尼的自由振动系统,方程为

其中,
- ω n = k m ——无阻尼固有圆频率 \omega_n=\sqrt{\frac{k}{m}}——无阻尼固有圆频率 ωn=mk——无阻尼固有圆频率
- C c = 2 k m ——临界阻尼系数(振荡和非振荡行为之间的阈值) C_c=2\sqrt{km}——临界阻尼系数(振荡和非振荡行为之间的阈值) Cc=2km——临界阻尼系数(振荡和非振荡行为之间的阈值)
- ζ = c / C c ——阻尼比 \zeta=c/C_c——阻尼比 ζ=c/Cc——阻尼比
- ω d = ω n 1 − ζ 2 ——阻尼震荡的频率 ( 有阻尼圆频率 ) \omega_d=\omega_n\sqrt{1-\zeta^2}——阻尼震荡的频率(有阻尼圆频率) ωd=ωn1−ζ2——阻尼震荡的频率(有阻尼圆频率)
每一阶模态下的上述参数都不一样。
如果复合材料的阻尼比较小,那么可以忽略阻尼进行分析,近似认为有阻尼固有频率=无阻尼固有频率,而无阻尼固有频率由结构的刚度和质量决定,进一步可知,复合材料层合板的密度,铺层厚度/顺序/方向,约束条件,接触条件都会影响到质量和刚度矩阵。相反,只要确定了这些条件,结构的固有频率,阻尼比(完整的阻尼矩阵一般很难求),振型等固有振动特性,就可以通过模态分析得到。
参与系数
参与系数——表示结构在某个方向上多大程度参与了振动。
第一阶模态的固有频率称之为基频,参与系数==贡献率。是为了找到结构在振动方向上起到关键作用的那阶固有频率(主要频率),参与系数可以从abaques的job monitor——data file 下查看。


有效质量
有效质量:参与结构振动的有效的质量,与参与系数平方成正比。有效质量大的更容易被激励。
abaques模态分析步骤和注意事项
模态分析假定是线性的,那么就不用考虑大变形,接触问题,材料非线性文章来源:https://www.toymoban.com/news/detail-801079.html
热载荷不能在模态分析中施加,但是热会影响材料属性。约束会影响结构的刚度矩阵,从而影响固有频率。文章来源地址https://www.toymoban.com/news/detail-801079.html
到了这里,关于【ABAQUS】模态分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!