论文阅读——《Retinexformer: One-stage Retinex-based Transformer for Low-light Image Enhancement》-Toy模板网

这篇具有很好参考价值的文章主要介绍了论文阅读——《Retinexformer: One-stage Retinex-based Transformer for Low-light Image Enhancement》。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

retinexformer: one-stage retinex-based transformer for low-light image enhan,1024程序员节,python,算法,图像处理,transformer,深度学习,论文阅读

前言

本文试图从原理和代码简单介绍低照度增强领域中比较新的一篇论文——Retinexformer，其效果不错，刷新了十三大暗光增强效果榜单。

❗论文名称：Retinexformer: One-stage Retinex-based Transformer for Low-light Image Enhancement

👀论文信息：由清华大学联合维尔兹堡大学和苏黎世联邦理工学院2023年8月发表在ICCV2023的一篇论文。
🎆论文地址：https://arxiv.org/abs/2303.06705
📌代码地址：https://github.com/caiyuanhao1998/Retinexformer
部分参考来源：https://zhuanlan.zhihu.com/p/657927878

论文主要贡献总结如下:
1.提出了首个与Retinex理论相结合的 Transformer 算法，命名为 Retinexformer。
2.推导了一个单阶段Retinex理论框架，名为 ORF（One-stage Retinex-based Framework），只需要一个阶段端到端的训练即可，流程简单。
3.设计了一种由光照引导的新型多头自注意机制，名为 IG-MSA（Illumination-Guided Multi-head Self-Attention，IG-MSA），将光照信息作为关键线索来引导长程依赖关系的捕获。

一、基本原理

首先看这个网络的名字——Retinexformer，我们基本就能知道主要是结合两个方面来设计的：

1.1 Retinex理论。

低照度增强领域中非常经典的理论，原理很简单，但是其应用范围非常广，很多的增强算法都是从该理论出发，包括之前介绍的SCI-Net也是从基于该理论。下面简单介绍一下该理论：
Retinex理论中将一幅图像 $S$ 看做是光照分量 $I$ 和反射分量 $R$ 的乘积，即
$\odot R$ $反射分量 R$ ： $物体的本身性质决定的恒定的部分$
$光照分量 I ：受外界光照影响的部分$
$\odot ：表示逐元素相乘$

1.2 Transformer 算法。

深度学习领域中必须提及的一个模型，其核心思想是将输入序列划分为多个子序列，并通过层级的编码-解码结构来处理这些子序列。它由编码器（Encoder）和解码器（Decoder）组成，每个部分都由多个相同的模块堆叠而成。
Transformer的原理部分可以参考：
- 大佬写的Transformer很详细
- 个人对部分代码的一些梳理

二、论文内容

尽管有很多的传统算法或者深度学习算法都是基于Retinex理论的，但是都没有考虑到噪声伪影等一些退化因素，只是直接应用上面的图像分解的式子，而本文的一个亮点就是将这些退化因素考虑在内。

1.网络结构

整个Retinexformer网络结构大体上分为两个部分：
- illumination estimator（光照估计模块）
- corruption restorer（退化修复器）
其中， corruption restorer主要由多个Illumination-Guided Attention Block（光照引导的注意力块，IGAB）组成；IGAB又由两个归一化层（LN）、一个前馈网络（FFN）和一个光照引导的多头自注意力模块（Illumination-Guided Multi-head Self-Attention，IG-MSA）组成。
注意：图中的 $I$ 相当于上面公式中的 $S$ , $L$ 才是光照量 $I$

1.1 单阶段Retinex理论框架（One-stage Retinex-based Framework）

根据上面的Retinex理论，若将噪声伪影等退化因素考虑在内,即在反射量和光照量中都加上扰动项。
$(R+\hat{R})\odot(I+\hat{I})=R\odot I+R\odot \hat{I}+\hat{R} \odot(I+\hat{I})$
为了提高暗光图像 $S$ 的亮度，两边同时乘上一个光照量 $\bar{I}$ ，并且使得 $\bar{I}\odot{I} = 1$ ，从而有：
$S\odot{\bar{I}}=R+R\odot(\hat{I}\odot \bar{I})+(\hat{R}\odot{(I+\hat{I})})\odot{\bar{I}}$
作者认为右边第二项 $R\odot(\hat{I}\odot \bar{I})$ 表示亮度增强过程中造成的曝光不足/过度曝光和色彩失真；而第三项中的 $(\hat{R}\odot{(I+\hat{I})})$ 表示隐藏在黑暗中的噪声和伪影，在亮度增强过程中（乘上 $\bar{I}$ ）会被进一步放大。
用 $C$ 表示所有的退化项， $S_{lu}$ 表示增强后的图像，有：
$S_{lu}=R+C$
ORF的过程可以表示为：
$(S_{lu}，F_{lu})=\varepsilon(S,I_{p})\\S_{en}=\mathcal{R}(S_{lu},F_{lu})$ $\varepsilon：表示light-up（增强）过程$
$S : 原始低照度图像$
$I_{p}：沿着通道维度计算每个像素的均值$
$F_{lu}：亮度的特征图$
$\mathcal{R}：损失修复器。重建过程，修复退化项$

1.2 illumination estimator

直接看代码部分：

class Illumination_Estimator(nn.Module):
    def __init__(
            self, n_fea_middle, n_fea_in=4, n_fea_out=3):  #__init__部分是内部属性，而forward的输入才是外部输入
        super(Illumination_Estimator, self).__init__()

        self.conv1 = nn.Conv2d(n_fea_in, n_fea_middle, kernel_size=1, bias=True)

        self.depth_conv = nn.Conv2d(
            n_fea_middle, n_fea_middle, kernel_size=5, padding=2, bias=True, groups=n_fea_in)

        self.conv2 = nn.Conv2d(n_fea_middle, n_fea_out, kernel_size=1, bias=True)

    def forward(self, img):
        # img:        b,c=3,h,w
        # mean_c:     b,c=1,h,w
        
        # illu_fea:   b,c,h,w
        # illu_map:   b,c=3,h,w
        
        mean_c = img.mean(dim=1).unsqueeze(1)
        # stx()
        input = torch.cat([img,mean_c], dim=1)

        x_1 = self.conv1(input)
        illu_fea = self.depth_conv(x_1)
        illu_map = self.conv2(illu_fea)
        return illu_fea, illu_map

1.3 光照引导的Transformer（Illumination-Guided Transformer，IGT）

retinexformer: one-stage retinex-based transformer for low-light image enhan,1024程序员节,python,算法,图像处理,transformer,深度学习,论文阅读

设计IGT的作用是用来表示上式中的 $\mathcal{R}$ ，用来修复退化项。
采用three-scale的U型架构（encoder-bottleneck-decoder）。
下采样过程中， $S_{lu}$ 经历一个 $3 \times 3 co n v$ 、一个 $I G A B$ 、一个 $4 \times 4 co n v (s t r i d e = 2)$ 、两个 $I G A B$ 、一个 $4 \times 4 co n v (s t r i d e = 2)$ ，得到分层特征 $F_{0}、F_{1}、F_{2}$ ，然后 $F_{2}$ 又通过两个IGAB。
设计对称结构作为上采样过程。经过上采样输出的是残差 $S_{re}$ 。最终输出的增强图像 $S_{en}=S_{lu}+S_{re}$ 。
代码实现部分：（个人感觉这部分代码在self.encoder部分和文中的结构貌似不太一致？不知道是不是自己理解错了😆）

class Denoiser(nn.Module):
    def __init__(self, in_dim=3, out_dim=3, dim=31, level=2, num_blocks=[2, 4, 4]):
        super(Denoiser, self).__init__()
        self.dim = dim
        self.level = level

        # Input projection
        self.embedding = nn.Conv2d(in_dim, self.dim, 3, 1, 1, bias=False)

        # Encoder
        self.encoder_layers = nn.ModuleList([])
        dim_level = dim
        for i in range(level):
            self.encoder_layers.append(nn.ModuleList([
                IGAB(
                    dim=dim_level, num_blocks=num_blocks[i], dim_head=dim, heads=dim_level // dim),
                nn.Conv2d(dim_level, dim_level * 2, 4, 2, 1, bias=False),
                nn.Conv2d(dim_level, dim_level * 2, 4, 2, 1, bias=False)
            ]))
            dim_level *= 2

        # Bottleneck
        self.bottleneck = IGAB(
            dim=dim_level, dim_head=dim, heads=dim_level // dim, num_blocks=num_blocks[-1])

        # Decoder
        self.decoder_layers = nn.ModuleList([])
        for i in range(level):
            self.decoder_layers.append(nn.ModuleList([
                nn.ConvTranspose2d(dim_level, dim_level // 2, stride=2,
                                   kernel_size=2, padding=0, output_padding=0),
                nn.Conv2d(dim_level, dim_level // 2, 1, 1, bias=False),
                IGAB(
                    dim=dim_level // 2, num_blocks=num_blocks[level - 1 - i], dim_head=dim,
                    heads=(dim_level // 2) // dim),
            ]))
            dim_level //= 2

        # Output projection
        self.mapping = nn.Conv2d(self.dim, out_dim, 3, 1, 1, bias=False)

        # activation function
        self.lrelu = nn.LeakyReLU(negative_slope=0.1, inplace=True)
        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    def forward(self, x, illu_fea):
        """
        x:          [b,c,h,w]         x是feature, 不是image
        illu_fea:   [b,c,h,w]
        return out: [b,c,h,w]
        """

        # Embedding
        fea = self.embedding(x)

        # Encoder
        fea_encoder = []
        illu_fea_list = []
        for (IGAB, FeaDownSample, IlluFeaDownsample) in self.encoder_layers:
            fea = IGAB(fea,illu_fea)  # bchw
            illu_fea_list.append(illu_fea)
            fea_encoder.append(fea)
            fea = FeaDownSample(fea)
            illu_fea = IlluFeaDownsample(illu_fea)

        # Bottleneck
        fea = self.bottleneck(fea,illu_fea)

        # Decoder
        for i, (FeaUpSample, Fution, LeWinBlcok) in enumerate(self.decoder_layers):
            fea = FeaUpSample(fea)
            fea = Fution(
                torch.cat([fea, fea_encoder[self.level - 1 - i]], dim=1))
            illu_fea = illu_fea_list[self.level-1-i]
            fea = LeWinBlcok(fea,illu_fea)

        # Mapping
        out = self.mapping(fea) + x

        return out

IG-MSA是这一部分的核心。
illumination estimator输出的亮度特征图 $F_{lu}$ 作为每一个IG-MSA的输入。首先 $F_{lu}$ 变形为token，然后被分成K个heads：
$X=[X_{1},X_{2},...,X_{k},]$ 对每个heads将其投影为 $Q ， K ， V$
$Q_{i}=X_{i}W^{T}_{Q_{i}}，K_{i}=X_{i}W^{T}_{K_{i}}，V_{i}=X_{i}W^{T}_{V_{i}}$
将 $F_{lu}$ 又变形成 $Y$ ： $Y=[Y_{1},Y_{2},...,Y_{k},]$

计算每个 head的自注意力时用光照信息作为引导：
retinexformer: one-stage retinex-based transformer for low-light image enhan,1024程序员节,python,算法,图像处理,transformer,深度学习,论文阅读

代码：

class IG_MSA(nn.Module):
    def __init__(
            self,
            dim,
            dim_head=64,
            heads=8,
    ):
        super().__init__()
        self.num_heads = heads
        self.dim_head = dim_head
        self.to_q = nn.Linear(dim, dim_head * heads, bias=False)
        self.to_k = nn.Linear(dim, dim_head * heads, bias=False)
        self.to_v = nn.Linear(dim, dim_head * heads, bias=False)
        self.rescale = nn.Parameter(torch.ones(heads, 1, 1))
        self.proj = nn.Linear(dim_head * heads, dim, bias=True)
        self.pos_emb = nn.Sequential(
            nn.Conv2d(dim, dim, 3, 1, 1, bias=False, groups=dim),
            GELU(),
            nn.Conv2d(dim, dim, 3, 1, 1, bias=False, groups=dim),
        )
        self.dim = dim

    def forward(self, x_in, illu_fea_trans):
        """
        x_in: [b,h,w,c]         # input_feature
        illu_fea: [b,h,w,c]         # mask shift? 为什么是 b, h, w, c?
        return out: [b,h,w,c]
        """
        b, h, w, c = x_in.shape
        x = x_in.reshape(b, h * w, c)
        q_inp = self.to_q(x)
        k_inp = self.to_k(x)
        v_inp = self.to_v(x)
        illu_attn = illu_fea_trans # illu_fea: b,c,h,w -> b,h,w,c
        q, k, v, illu_attn = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=self.num_heads),
                                 (q_inp, k_inp, v_inp, illu_attn.flatten(1, 2)))
        v = v * illu_attn
        # q: b,heads,hw,c
        q = q.transpose(-2, -1)
        k = k.transpose(-2, -1)
        v = v.transpose(-2, -1)
        q = F.normalize(q, dim=-1, p=2)
        k = F.normalize(k, dim=-1, p=2)
        attn = (k @ q.transpose(-2, -1))   # A = K^T*Q
        attn = attn * self.rescale
        attn = attn.softmax(dim=-1)
        x = attn @ v   # b,heads,d,hw
        x = x.permute(0, 3, 1, 2)    # Transpose
        x = x.reshape(b, h * w, self.num_heads * self.dim_head)
        out_c = self.proj(x).view(b, h, w, c)
        out_p = self.pos_emb(v_inp.reshape(b, h, w, c).permute(
            0, 3, 1, 2)).permute(0, 2, 3, 1)
        out = out_c + out_p

        return out

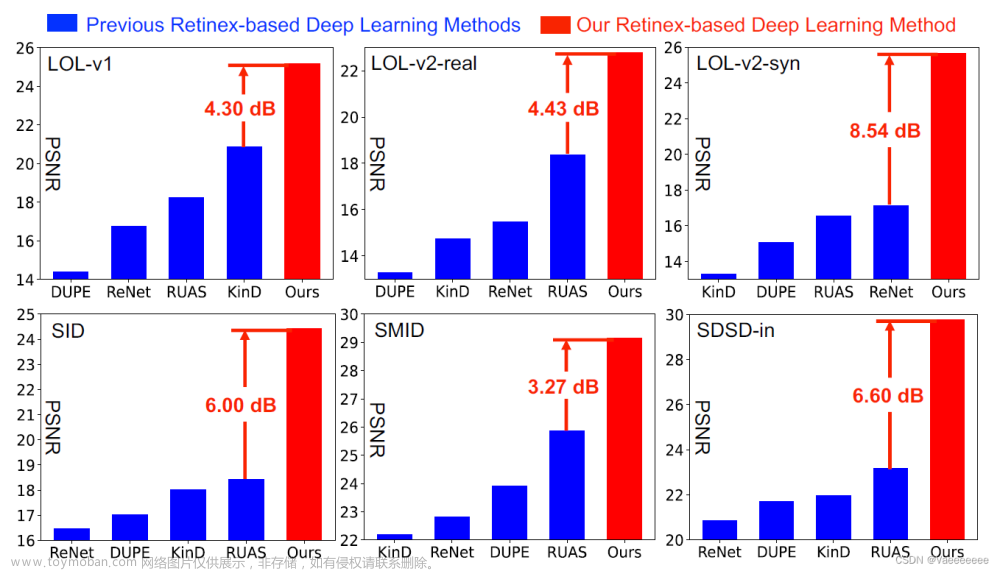
实验结果

retinexformer: one-stage retinex-based transformer for low-light image enhan,1024程序员节,python,算法,图像处理,transformer,深度学习,论文阅读

个人看法

只给了PSNR和SSIM两个评价指标，缺少一些无参考图像质量评价。
实际测试的效果发现图片中较亮的区域很容易出现过曝和色彩失真的问题：
测试图片增强前后
- example 1
- example 2
  
  文章来源地址https://www.toymoban.com/news/detail-801143.html

总结

Retinexformer通过分析低曝光场景中隐藏的噪声伪影以及点亮过程带来的影响，将扰动项引入到原始的Retinex模型中，构建了一个新的基于Retinex的框架ORF。然后设计了一个利用ORF捕获的光照信息来指导不同光照条件下区域的长程依赖和相互作用的IGT。最后通过将IGT插入到ORF中得到了完整的Retinexformer模型。

到了这里，关于论文阅读——《Retinexformer: One-stage Retinex-based Transformer for Low-light Image Enhancement》的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！