机器学习之伯努利分布及二项分布

8月前作者：WEL测试分类：Toy博客阅读(59) 违法举报

这篇具有很好参考价值的文章主要介绍了机器学习之伯努利分布及二项分布。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

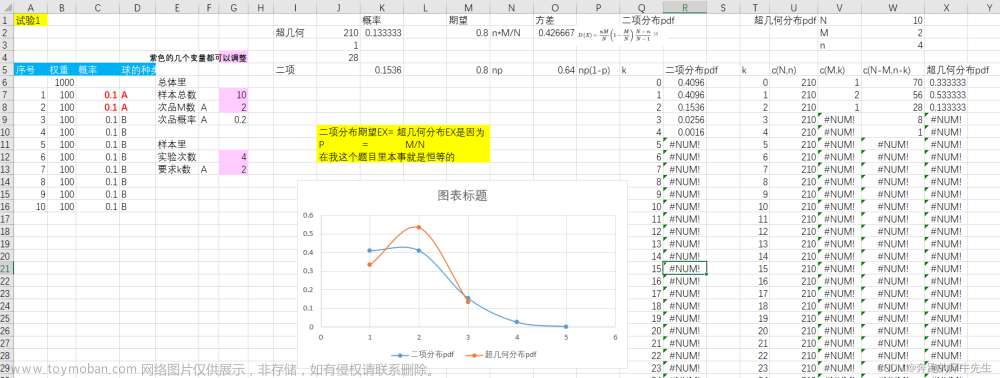
伯努利分布：又称两点分布或0-1分布，其样本空间只有两个点，一般取{0，1}，不同的伯努利分布只是取到这两个值的概率不一样。伯努利分布只有一个参数p（用描述取1的概率），记作 $B er n o u ll (p)$ 或 $X$ ~ $B (p)$ 读作X服从参数为p的伯努利分布。参数p是通过大量重复的伯努利试验计算的来的。公式： $p = 1 - q$ ，q表示为1的概率。期望为：p，方差为：p(1-p)文章来源地址https://www.toymoban.com/news/detail-801283.html

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
def bern(p=0.3):
 ber_dist=stats

到了这里，关于机器学习之伯努利分布及二项分布的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

伯努利分布

伯努利分布（Bernoulli Distribution），是一种离散分布，又称为 “0-1 分布” 或 “两点分布”。在讲伯努利分布前首先需要介绍伯努利试验（Bernoulli Trial）。伯努利试验是只有两种可能结果的单次随机试验，即对于一个随机变量 X： P [ X = 1 ] = p P [ X = 0 ] = 1 − p P[X=1]=p\\\\ P[X=0

2024年02月01日
浏览(21)
机器学习-朴素贝叶斯（高斯、多项式、伯努利）

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。贝叶斯分类器主要思想是基于贝叶斯定理，是机器学习中重要的分类算法，适用于高维度的大数据集，速度快，准确率高，一个经典的应用场景是识别垃圾邮件。

2023年04月09日
浏览(60)
（矩阵）一阶微分方程和伯努利方程

伯努利方程的标准形式：伯努利方程解法：方程两边同时除以y的n次，做变量替换y-z：转换为线性微分方程：最后换回原来的变量即可得到伯努利方程。一阶线性微分方程的标准形式：当Q(x)=0，为齐次方程；当Q(x)≠0，为非齐次方程。已知如下矩阵，求解一阶线性微分方

2024年02月05日
浏览(41)
机器学习之泊松分布及均匀分布

泊松分布适合描述单位时间或单位面积内随机事件的平均发生率。泊松分布的概率质量函数为： P ( X = k ) = e − λ λ k / k ! P(X=k)=e^{-lambda} lambda^k/k! P ( X = k ) = e − λ λ k / k ! 参数 λ 是单位时间（或单位面积）内随机事件的平均发生频率。把一个随机变量X服从参数为λ的泊

2024年01月22日
浏览(24)
初识人工智能，一文读懂机器学习之逻辑回归知识文集(1)

🏆作者简介，普修罗双战士，一直追求不断学习和成长，在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验，历任核心研发工程师，项目技术负责人。 🎉欢迎 👍点赞✍评论⭐收藏 🔎 人工智能领域知识 🔎 链接专栏人工智能专业知识学习一人工智能专栏人

2024年01月23日
浏览(48)
负二项分布（一种离散分布）

负二项分布是伯努利分布的推广，它模拟了在指定（非随机）失败次数（表示为r）发生之前，一系列独立且同分布的伯努利试验中的成功次数负二项分布可以用来确定一个系列中多于1次失败的概率比如：计算一台机器彻底崩溃前的天数、输掉系列赛冠军需要进行多少场比赛

2024年02月15日
浏览(29)
二项分布习题

习题： X ～ B（n，p），n = 5, p = 0.25, k = (0 ～ n)。将 n , k , p 代入函数：解：输出为：一射手向目标独立地进行了3次射击，每次击中率为0.8，求3次射击中击中目标的次数的分布律，并求3次射击中至少击中2次的概率。解：设 X 表示击中目标的次数，则 X = 0， 1， 2， 3。

2024年02月06日
浏览(22)
【分布族谱】正态分布和二项分布的关系

正态分布，最早由棣莫弗在二项分布的渐近公式中得到，而真正奠定其地位的，应是高斯对测量误差的研究，故而又称Gauss分布。测量是人类定量认识自然界的基础，测量误差的普遍性，使得正态分布拥有广泛的应用场景，或许正因如此，正太分布在分布族谱图中居于核心的

2024年02月05日
浏览(34)
二项分布的极大似然估计

笔记来源：Maximum Likelihood for the Binomial Distribution, Clearly Explained!!! P ( x ∣ n , p ) P(x|n,p) P ( x ∣ n , p ) 计算二项分布的极大似然估计 L ( p ∣ n , x ) L(p|n,x) L ( p ∣ n , x )

2024年02月11日
浏览(48)
概率论的学习和整理15：超几何分布，二项分布，泊松分布是如何趋近收敛的?

目录 1 问题： 2 结论 3 实验1 4 实验2 5 实验3 6 实验4 5 各种规律总结 5.1 1 5.2 2 5.3 3 5.4 4 6 超几何分布，二项分布，泊松分布，三者用EXCEL模拟 6.1 简单的扩展到泊松分布 6.2 比较整体的动态过程，增加实验次数时从一个简单模型说开去比如，有10个球，其中有x个

2024年02月16日
浏览(28)