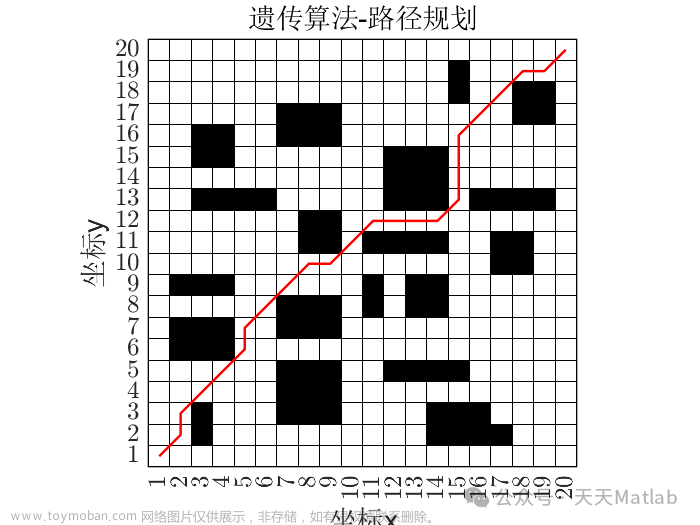
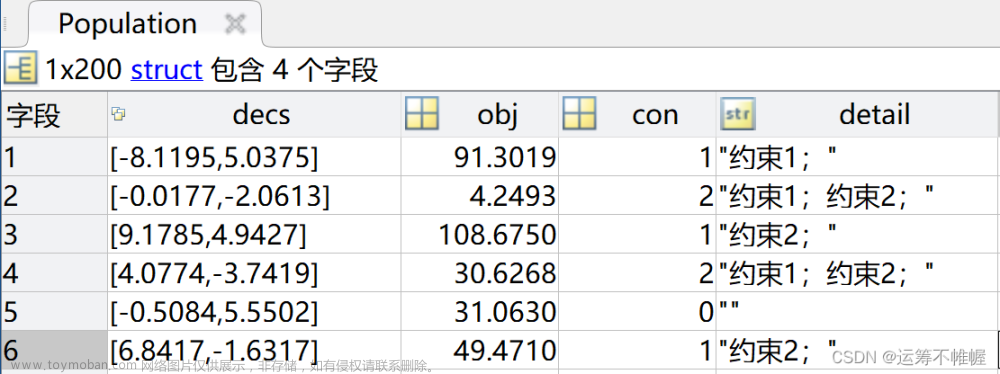
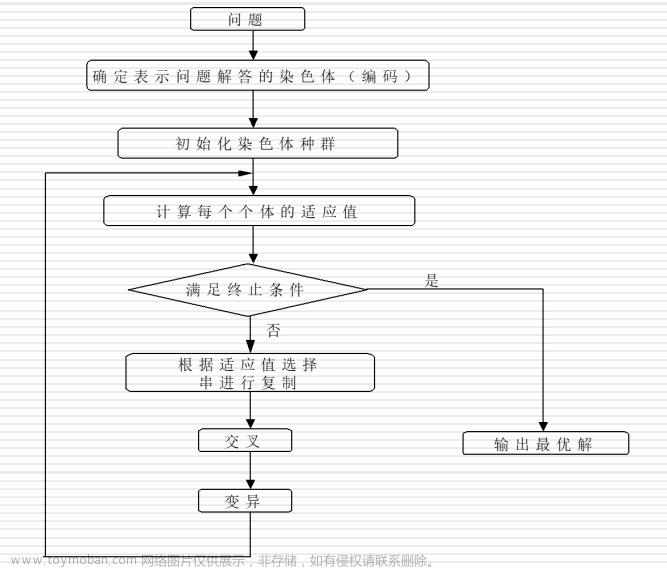
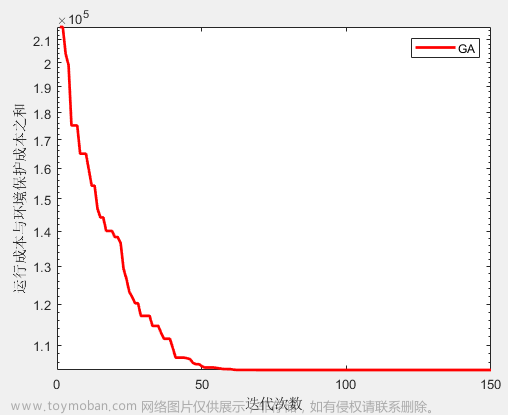
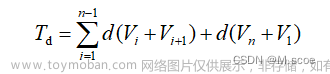遗传算法求解车辆路径优化问题VRP（Python代码实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了遗传算法求解车辆路径优化问题VRP（Python代码实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

学会了前面两篇遗传算法，但是那都是针对抽象的数学问题求解的，那么应用到现实中的实际问题中，我们又该怎样把遗传算法套进去呢，然后我第一个接触到的问题就是车辆路径优化问题VRP，当然也是找到了一篇比较好的文章，物流管理论文实现：基于遗传算法的带时间窗和载重约束的车辆路径优化
这位博主的代码写的非常不错，因为我复制过来运行的时候没有报错，但是，看的时候也比较费劲，因为这个博主比较厉害，他在里面定义了一个类class，然后就会有很多self，与普通的定义函数有了些许的差别，导致我这种小白，看起来特别不舒服，不知道具体的选择、交叉和变异操作是怎么实现的，所以我就凭借前两篇的学习和自己的理解，把代码重新写了一遍，其中目标函数原本比较复杂，也被我简化了，只需要求距离最短即可，因为我就想看一下这个遗传算法套在实际问题里的样子，当然越简单越好，我觉得我能看懂，大部分人应该都可以了。
而且在这个过程中，还学会了一个技巧，在出现错误运行不下去的时候，就加个try，except，把错误跳过去，继续运行，就能得出结果了。
先定义一下问题里给的条件，初始化参数

geneNum = 100  # 种群数量
generationNum = 300  # 迭代次数


CENTER = 0  # 配送中心

# HUGE = 9999999
# PC = 1   #交叉率,没有定义交叉率，也就是说全部都要交叉，也就是1
PM = 0.1  # 变异率   以前是用的vary

n = 25  # 客户点数量
m = 2  # 换电站数量
k = 3  # 车辆数量
Q = 5  # 额定载重量, t
# dis = 160  # 续航里程, km
length = n+m+1

# 坐标   第0个是配送中心   1-25是顾客      26和27是换电站          一共28个位置    行驶距离要通过这个坐标自己来算
X = [56, 66, 56, 88, 88, 24, 40, 32, 16, 88, 48, 32, 80, 48, 23, 48, 16, 8, 32, 24, 72, 72, 72, 88, 104, 104, 83,32]
Y = [56, 78, 27, 72, 32, 48, 48, 80, 69, 96, 96, 104, 56, 40, 16, 8, 32, 48, 64, 96, 104, 32, 16, 8, 56, 32, 45, 40]
# 需求量
t = [0, 0.2, 0.3, 0.3, 0.3, 0.3, 0.5, 0.8, 0.4, 0.5, 0.7, 0.7, 0.6, 0.2, 0.2, 0.4, 0.1, 0.1, 0.2, 0.5, 0.2, 0.7,0.2,0.7, 0.1, 0.5, 0.4, 0.4]

编码：根据实际问题来编码，那就采用实数编码好了，需要求得内容都放到染色体里面
分两步才能产生符合条件的初始个体，先产生无序列表，并在首尾位置插入配送中心0，然后再根据一辆车运输的需求量总和不超过车的负载，往这个无序列表里面随机插入0作为从配送中心新的开始，也就表示了有几辆车
注意：这里产生初始种群就不像前两篇的纯数学问题那么简单了，还要写成一个函数，才能产生满足要求的初始解，也就是初始种群。

def getGene(length):   
    ##先产生一个无序的列表
    data = list(range(1,length))  ##先产生一个有序的列表
    np.random.shuffle(data)   ##有序列表打乱成无序列表
    data.insert(0, CENTER)    ##在开始插入0
    data.append(CENTER)       ##在结尾插入0

    #再插入车
    sum = 0
    newData = []
    for index, pos in enumerate(data):
        sum += t[pos]
        if sum > Q:
            newData.append(CENTER)
            sum = t[pos]
        newData.append(pos)

    return newData
def getpop(length,geneNum):
    pop = []
    for i in range(geneNum):
        gene = getGene(length)
        pop.append(gene)
    return pop

计算适应度值，计算一个个体的适应度值,然后得到整个种群的适应度列表
注意：适应度值就是距离函数，需要根据各个点的坐标自己表示出来

##计算一个个体的适应度值
def getfit(gene):
    distCost = 0
    dist = []  # from this to next
    # 计算距离
    i = 1
    while i < len(gene):
        calculateDist = lambda x1, y1, x2, y2: math.sqrt(((x1 - x2) ** 2) + ((y1 - y2) ** 2))
        dist.append(calculateDist(X[gene[i]], Y[gene[i]], X[gene[i - 1]], Y[gene[i - 1]]))
        i += 1
    # 距离成本
    distCost = sum(dist)     #总行驶距离
    fit = 1/distCost   ##fitness越小表示越优秀，被选中的概率越大，
    return fit
##得到整个种群的适应度列表
def getfitness(pop):
    fitness = []
    for gene in pop:
        fit = getfit(gene)
        fitness.append(fit)
    return np.array(fitness)

选择，利用轮盘赌，适应度值越大越有可能被选择出来到下一代

def select(pop,fitness):
    fitness = fitness / fitness.sum()  # 归一化
    idx = np.array(list(range(geneNum)))
    pop_idx = np.random.choice(idx, size=geneNum, p=fitness)  # 根据概率选择
    for i in range(geneNum):
        pop[i] = pop[pop_idx[i]]
    return pop

这里的交叉也比较麻烦，因为在这个问题里面不能随便交叉，因为如果你用5交叉换回来一个6，但是其实这个个体里面已经有6了，每个客户只能拜访一次，这就不符合问题规定了，所以要进行一些操作铺垫
选择路径实现的效果如下：
车辆路径遗传算法python,python,算法
然后再是两个个体的交叉，效果如下：

拿gene1来说，就是把gene2里面有的，但是gene1前面那个路径里面没有的数字加到gene1的后面，得到newgene1，newgene2也是同理，然后就交叉完了。

并且只选择了适应度较高的前1/3种群进行交叉，不用交叉概率的，所有的都要交叉，但是交叉完得到的种群也只有1/3的个体，所以再把这1/3的个体替换到原种群最后面适应度较低的那一部分，最终合并成一个完整的种群。

#选择路径
def moveRandSubPathLeft(gene):
    import random
    path = random.randrange(k)  # 选择路径索引，随机分成k段
    print('path:',path)
    try:
        index = gene.index(CENTER, path+1) #移动到所选索引
        # move first CENTER
        locToInsert = 0
        gene.insert(locToInsert, gene.pop(index))
        index += 1
        locToInsert += 1
        # move data after CENTER
        print('index:',index)
        try:
            print('len(gene):',len(gene))
            while gene[index] != CENTER:
                gene.insert(locToInsert, gene.pop(index))
                index += 1
                print('执行完index+1,index=',index)
                locToInsert += 1
            return gene
            # assert(length+k == len(gene))
        except:
            print('出错啦，index:',index)
            return gene
    except:
        print('0 is not in list',gene)
        return gene

# 选择复制，选择适应度最高的前 1/3，进行后面的交叉
def choose(pop):
    num = int(geneNum/6) * 2    # 选择偶数个，方便下一步交叉
    # sort genes with respect to chooseProb
    key = lambda gene: getfit(gene)
    pop.sort(reverse=True, key=key)      ##那就是说按照适应度函数降序排序,选了适应度值最高的那1/3
    # return shuffled top 1/3   
    return pop[0:num]

交叉这个就不考虑交叉概率了，因为轮流所有的都会交叉，但是代码先写交叉一对，再把前面选择出来的适应度较高的前1/3种群进行交叉

##交叉一对
def crossPair(i,gene1, gene2, crossedGenes):
    gene1 = moveRandSubPathLeft(gene1)
    gene2 = moveRandSubPathLeft(gene2)
    newGene1 = []
    newGene2 = []
    # copy first paths
    centers = 0
    firstPos1 = 1
    for pos in gene1:
        firstPos1 += 1
        centers += (pos == CENTER)
        newGene1.append(pos)
        if centers >= 2:
            break
    centers = 0
    firstPos2 = 1
    for pos in gene2:
        firstPos2 += 1
        centers += (pos == CENTER)
        newGene2.append(pos)
        if centers >= 2:
            break
    # copy data not exits in father gene
    for pos in gene2:
        if pos not in newGene1:
            newGene1.append(pos)
    for pos in gene1:
        if pos not in newGene2:
            newGene2.append(pos)
    # add center at end
    newGene1.append(CENTER)
    newGene2.append(CENTER)
    # 计算适应度最高的
    key1 = lambda gene1: getfit(gene1)
    possible1 = []
    try:
        while gene1[firstPos1] != CENTER:
            newGene = newGene1.copy()
            newGene.insert(firstPos1, CENTER)
            possible1.append(newGene)
            firstPos1 += 1
        print('第{}位置:{}'.format(i,len(possible1)))
        if len(possible1) == 0:
            crossedGenes.append(newGene1)
        else:
            possible1.sort(reverse=True, key=key1)
            crossedGenes.append(possible1[0])
    except:
        print('交叉出错啦：firstPos1', firstPos1)

    key2 = lambda gene2: getfit(gene2)
    possible2 = []
    try:
        while gene2[firstPos2] != CENTER:
            newGene = newGene2.copy()
            newGene.insert(firstPos2, CENTER)
            possible2.append(newGene)
            firstPos2 += 1
        print('第{}:{}'.format(i,len(possible2)))
        if len(possible2) == 0:
            crossedGenes.append(newGene2)
        else:
            possible2.sort(reverse=True, key=key2)
            crossedGenes.append(possible2[0])
        print('交叉完成第：', i)
    except:
        print('交叉出错啦：',i)

# 交叉
def cross(genes):
    crossedGenes = []
    for i in range(0, len(genes), 2):
        # print('gene[i]:',genes[i])
        # print('gene[i+1]:', genes[i])
        crossPair(i,genes[i], genes[i+1], crossedGenes)
        print('交叉完成')
    return crossedGenes

# 合并
def mergeGenes(genes, crossedGenes):
    # sort genes with respect to chooseProb
    key = lambda gene: getfit(gene)
    genes.sort(reverse=True, key=key)    ##先把原来的种群100按照适应度降序排列，然后，将交叉得到的32个个体替换到种群的最后32个
    pos = geneNum - 1
    for gene in crossedGenes:
        genes[pos] = gene
        pos -= 1
    return  genes

变异，先写一下个体怎么变异，然后再根据变异概率对整个交叉完的种群变异
注意：这里的变异就很简单了，直接用产生初始种群中个体的方法产生一个新的个体，但是这里也采用了，多产生几个个体，选其中适应度最高的那个个体的方法来减小误差。

# 变异一个
def varyOne(gene):
    varyNum = 10    
    variedGenes = []
    for i in range(varyNum):       # 先按照这种方法变异10个，选择适应度最高的那个作为变异完的子代
        p1, p2 = random.choices(list(range(1,len(gene)-2)), k=2)
        newGene = gene.copy()
        newGene[p1], newGene[p2] = newGene[p2], newGene[p1] # 交换
        variedGenes.append(newGene)
    key = lambda gene: getfit(gene)
    variedGenes.sort(reverse=True, key=key)
    return variedGenes[0]

# 变异
def vary(genes):
    for index, gene in enumerate(genes):
        # 精英主义，保留前三十，这个意思就是前三十个一定不变异，到后面的个体才按照变异概率来变异
        if index < 30:
            continue
        if np.random.rand() < PM:
            genes[index] = varyOne(gene)
    return genes

遗传算法主体文章来源地址https://www.toymoban.com/news/detail-801689.html

import numpy as np
import random
from tqdm import *  # 进度条
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False

best_fitness = []
min_cost = []
J = []
pop = getpop(length, geneNum)  # 初始种群
# 迭代
for j in tqdm(range(generationNum)):
    print('j=',j)
    chosen_pop = choose(pop)   # 选择   选择适应度值最高的前三分之一，也就是32个种群，进行下一步的交叉
    crossed_pop = cross(chosen_pop)   # 交叉
    pop = mergeGenes(pop, crossed_pop) # 复制交叉至子代种群
    pop = vary(pop) # under construction
    key = lambda gene: getfit(gene)
    pop.sort(reverse=True, key=key)  # 以fit对种群排序
    cost = 1/getfit(pop[0])
    print(cost)
    min_cost.append(cost)
    J.append(j)
print(J)
print(min_cost)


# key = lambda gene: getfit(gene)
# pop.sort(reverse=True, key=key)   # 以fit对种群排序
print('\r\n')
print('data:', pop[0])
print('fit:', 1/getfit(pop[0]))
plt.plot(J,min_cost, color='r')
plt.show()