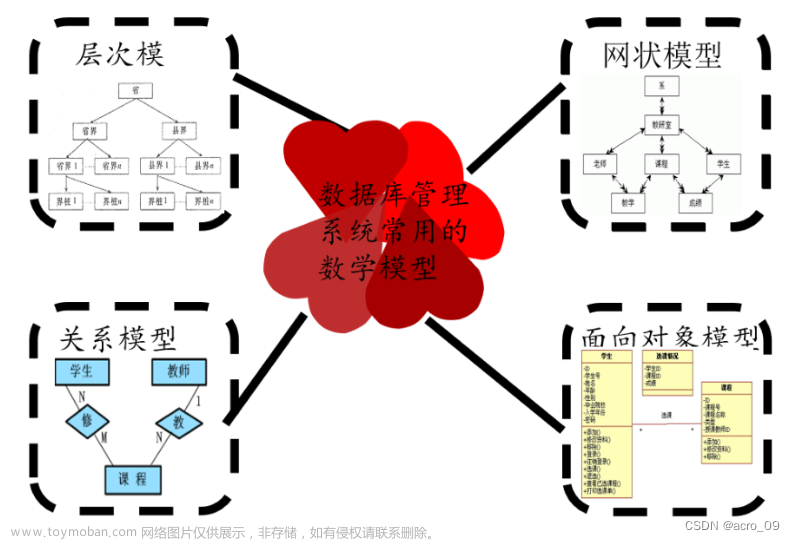
1. 引言
前序博客：
- 利用多核的Rust快速Merkle tree
Anoushk Kharangate 2023年论文《Asynchronous Merkle Trees》，其对Merkle tree数据结构进行修改，使得可跨多线程异步计算。
开源代码实现见：
- https://github.com/anoushk1234/async-merkle-tree（Rust）
Merkle tree应用广泛，有各种变种，如：
- Jellyfish Merkle Tree
- Sparse Merkle Tree
但这些都存在一个共同的问题：
- 当用Merkle Tree来处理大数据集时，计算该tree的开销，将大幅增加。此外，插入单个叶子节点，将需要重构整棵树。
在某些情况下，插入叶子节点时的计算时间，应尽可能短，且对于数据并行处理的场景，需要能异步计算。《Asynchronous Merkle Trees》论文中：
- 提出了并行处理一组数据，批量异步所构建的Merkle Tree，在每次插入时，无需重新计算该tree。
2. Asynchronous Merkle Trees（AMT）
Asynchronous Merkle Trees（AMT）有如下关键属性：
- 1）节点类型：包含3种特殊节点：
- 1.1）Digest节点：仅简单用作另一batch node的placeholder。
- 1.2）Layer Checkpoint（LC）节点
- 1.3）Compound节点：
- 2个LC节点组成一个Compound节点。
- 一个LC节点和一个Compound节点，组成另一Compound节点。
- 2）排序：每个特殊节点必须包含一个order bit，以表示是其父节点的左子节点，还是右子节点。
- 3）Segregation隔离：每个节点必须有一个batch bit，以表示其属于哪个batch。
某Merkle Tree T T T，其遵循如下要求：
- 1） T T T的高度为 h h h，其中 h = log 2 ( n ) h=\log_2(n) h=log2(n)， n n n为叶子节点数
- 2） T T T必须最多有 M M M个节点，其中 M = ∑ n h n 2 M=\sum_{n}^{h}\frac{n}{2} M=∑nh2n
- 3）叶子节点表示为 N i N_i Ni，其中 { i ∈ N ∣ 0 ≤ i ≤ 2 D } \{i\in N|0\leq i \leq 2^D\} {i∈N∣0≤i≤2D}
将以上Merkle Tree T T T，扩展为，创建AMT，其遵循如下要求：
- 1）异步附加的叶子称为Batches B B B，batches的数量和其叶子必须提取已知。
- 2）以大量Digest Nodes D i D_i Di来初始化该tree，Digest Nodes D i D_i Di用作其它batches节点的placeholder。
如上图所示，以3层Merkle tree为例，当附加红色batch叶子时，需重新计算
N
11
N_{11}
N11和
N
12
N_{12}
N12，无法异步附加。
对应的AMT为4层：
对应每个节点必须包含如下数据：文章来源：https://www.toymoban.com/news/detail-801880.html
- 1）Batch：一个整数值，用于表示该节点属于哪个batch
- 对于Compound节点，可将其设置为（与现有batch id不冲突的）某特殊整数值，来表示该节点不属于特定batch。
- 2）Order：一个整数值，为0或1，以表示左节点或右节点。
- 3）Data：实际的数据哈希值。
文章来源地址https://www.toymoban.com/news/detail-801880.html
Merkle tree系列博客
- 利用多核的Rust快速Merkle tree
- Merkle tree proof
- Merkle tree及其在区块链等领域的应用
- Sparse Merkle Tree
- 以太坊EIP-1186：RPC-Method to get Merkle Proofs - eth_getProof
- proof of solvency（偿付能力证明）方案
- 以太坊中的modified Merkle Patricia Trie
- 以太坊Eth2 deposit merkle tree
- Polygon zkEVM中的Merkle tree
- Merkle tree for non-membership proof
- Polygon zkEVM Merkle tree的circom约束
- Zcash中的merkle tree
到了这里，关于异步Merkle Tree的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
