GAN 论文阅读笔记（6）-Toy模板网

这篇具有很好参考价值的文章主要介绍了GAN 论文阅读笔记（6）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

原论文：MyStyle++: A Controllable Personalized Generative Prior
发表于：CVPR2023

注：本篇论文为《MyStyle: A Personalized Generative Prior》的改进，当遇到不理解的地方可以参照前一篇阅读笔记

图 1：MyStyle++ 在图像合成，编辑和增强上的表现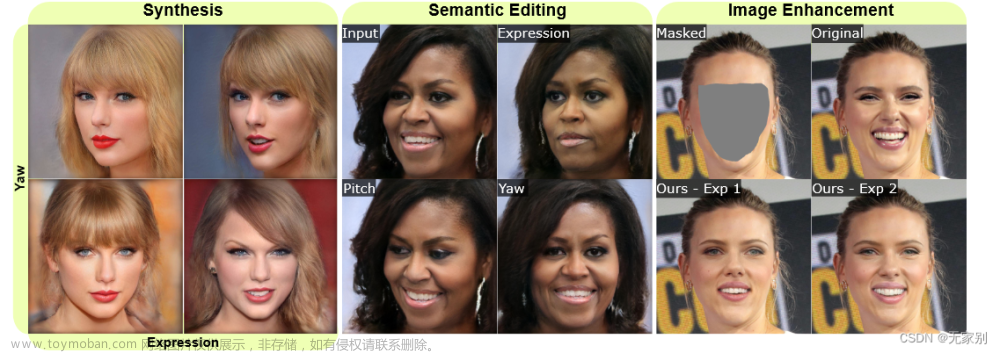
GAN 论文阅读笔记（6）,GANNNNNN！！！,生成对抗网络,论文阅读,笔记

1：MyStyle

MyStyle 是一种 GAN 模型的改进模型。其打算通过个性化感兴趣的个体的生成先验来解决 GAN 模型 (如 StyleGAN 等) 无法保留目标人物的身份和关键面部信息的问题。

具体来说，给定一个人的几张图像，MyStyle 首先将这些图像投影到预训练 StyleGAN 的潜在空间中，以获得一组潜在向量，称为锚点。然后，它通过最小化合成锚图像与其相应输入图像之间的误差来调整生成器。通过这个过程，生成器变得高度调谐，在锚点覆盖的潜在空间的特定区域以高保真度重建感兴趣的个体特征。

MyStyle 有着十分强力的个性化能力，其生成的图像保留了目标个体的身份和面部特征，可以用于各种任务，如合成、语义编辑和图像增强等等。

2：MyStyle 的不足之处

尽管 MyStyle 的使 GAN 拥有个性化的能力十分的强大，但它只关注了图像的身份保持能力，即这幅图像是我们想要生成的那个人的图像，而没有对某些属性（如姿势、表情）的调节能力。

图 2：
GAN 论文阅读笔记（6）,GANNNNNN！！！,生成对抗网络,论文阅读,笔记

对于图像编辑，MyStyle 使用诸如 InterFaceGAN 等方法提供的编辑方向，以提供对生成图像属性的可控性。由于这些编辑方向是在整个领域中学习的，因此它们可能不在个性化子空间中。如图2 ( 最上方一行 ) 所示，通过使用原始方向进行编辑，潜在代码将迅速落在个性化子空间之外，产生具有不同身份的图像。为了解决这个问题，MyStyle通过添加一个损失函数将编辑方向投射 ( 约束 ) 到子空间来个性化编辑方向。虽然投影编辑方向将潜在代码保留在个性化子空间中，但它失去了执行解纠缠编辑的能力。如图2( 中 )所示，去掉表达式也会改变偏航角 ( yaw angle )。在这里的表现为：虽然实现了去掉人物笑容的目标，但因为属性之间未能解纠缠而导致了人物的姿态，头发形状等属性也随着发生了改变。

3：MyStyle++

作为 MyStyle 的改进，MyStyle++ 有相当一部分是和 MyStyle 一样的，包括剪裁、对齐和调整图像大小等预处理步骤。

而对于如何对生成图像的属性的精确控制，作者主要通过根据一组预定义属性组织个性化子空间来解决这个问题。

作者为每张图像估计一组共 M 个预定义属性 ( 例如偏航角 yaw 和表达式 ) 。其中属性可以分为是离散的又或是连续的 ( 具有离散域或者连续域 )。保留离散属性不变，但将连续属性的范围量化为 $a_{m,p}$ , 其中 $m$ ( $m\in\{ 1,...,M\}$ ) 为属性类型， $p$ $(p\in\{ 1,...,P(m)\})$ 为属性值的索引。每个属性m的量化层次数P (m)可以不同。然后将每个图像的估计属性归属到最接近的量化值。

图 3：连续属性的范围量化示例
GAN 论文阅读笔记（6）,GANNNNNN！！！,生成对抗网络,论文阅读,笔记

示例中的横轴为人物朝向 ( 姿势 ) 的属性，而纵轴为人物表情的属性。我们可以观察到不同分类下的图片个数是可以不一样的，属性的划分层数也可以是不一样的。

3.1：可控制的个性化

MyStyle 通过将图片映射到 StyleGAN 的潜空间形成一组 N 个锚，记为 $\{w_{n}\}^{N}_{n=1}$ . 这一组 N 个锚点所围成的凸包就是 MyStyle 所希望得到的个性化子空间。而在 MyStyle++ 中，作者除了调整生成器以保持和提高其对目标个体的保真度外，还希望组织潜空间以完全控制一组属性。

作者的一个关键观察是，我们可以通过重新排列锚点来组织潜空间。这是因为 StyleGAN 的输出相对于输入变化地平滑，因此当锚移动时，它的邻域将被拖拽。在此基础上，我们制定了一个锚损失，根据锚的属性对锚进行重新排列。

原文：
Our key observation is that we can organize the latent space by only rearranging the anchors. This is because the output of StyleGAN changes smoothly with respect to the input, and thus as an anchor moves, its neighborhood will be dragged with it. Based on this observation, we formulate an anchor loss to rearrange the anchors based on their attributes.

为使得属性可编辑，我们应当满足以下三个属性：

每个属性应该沿着已知的方向变化。 $d_{m}$ 表示 $m^{th}$ 属性 ( 第 m 个属性 )。这是为了确保我们可以执行语义编辑，并通过简单地沿着属性方向修改潜在代码来更改特定属性。
沿一个属性方向投射到相同值的所有潜码应具有相同的属性。例如，所有沿偏航方向投影到 0.5的潜码都应该对应于正面的图像。这允许我们通过确保潜在代码沿着每个属性方向投射到适当的值，直接对具有特定属性集的图像进行采样。
不同属性的方向应该是正交的，以保证属性完全解缠，改变一个属性不会导致其他属性的改变。

作者将这三种属性 ( 要求 ) 整理为以下损失函数:

$L_{anc}=\sum_{m=1}^{M}L_{d}(d_{m})$

其中：

$L_{d}=\sum_{n=1}^{N}||w_{n}\cdot d_{m}-c_{n,m}||$

在这里的 $w_{n}\cdot d_{m}$ 为通过点积计算第 n 张图片的锚点在第 $m$ 个属性方向上的投影； $c_{n,m}$ 为与第 n 张图像具有相同第 m 个属性的所有图像 ( 子集记为 $N_{n,m}$ ) 在 $d_{m}$ 方向上投影锚点的平均值，可以由下式计算：

$c_{n,m}=\frac{1}{|N_{n,m}|}\sum_{k\in N_{n,m}}w_{k}\cdot d_{m}$

其中：

$N_{n,m}={k\in \{1,...,N\}}|k\ne n,f_{a}(I_{n}[m])=f_{a}(I_{k})[m])$

其中 $f_{a}(I_{n}[m])$ 返回图像 $I_n$ 的量化第 m 个属性。

简单的组合一下上面的几个式子有：

$L_{anc}=\sum_{m=1}^{M}\sum_{n=1}^{N}||w_{n}\cdot d_{m}-c_{n,m}||$

这个公式是十分像均值聚类的公式的：同样是各个点减去其均值。在这里可以这么理解这个损失函数：最小化这个损失函数就是在最小化各个锚的投影间的距离，即使得个性子空间尽可能的小，最终收缩至同一个点。

可以预见的是 $c_{n,m}$ 在每次迭代中都会变化。通过优化以上的损失函数，我们可以确保所有具有相同第 m 个属性的锚都会沿着第 m 个属性方向 $d_{m}$ 投射到同一点。这样我们就可以满足之前所提到的三个属性中的第二点，即：沿一个属性方向投射到相同值的所有潜码应具有相同的属性。

这个损失函数还确保了每个属性沿着其已知且特定的方向改变，从而满足三个属性中的第一点。

为了满足第三个属性，作者对所有 $N$ 个锚点应用主成分分析法 ( PCA ) ，并使用主成分的一个子集作为 $d_m$ 。我们通过优化以下目标为每个 $d_m$ 分配一个特定的主成分:

$d_{m}=\arg \min_{v_{i}\in V}L_{d}(v_{i})$

这里的 $V$ 为所有主分量的集合； $L_{d}$ 与之前的定义相同。

这里作者使用了 PCA 来找到主要属性，但我们了解一些 GAN 的都知道有个 PCA 的上位替代品：SeFa 同样可以做到主成分分析的功能，而且是为了 GAN 而定制的。笔者认为在这里使用 SeFa 可能是个更好的选择，就算不是，PCA 和 SeFa 在这里的性能区别也是个可以讨论的点。

SeFa 相关可以参考之前写的 GAN论文阅读笔记中相关部分

在这里主要是希望通过在每次迭代中使用 PCA 来确保 潜空间 已经与 选定的方向 很好地对齐来执行最少的重排。因此，当我们在不同的迭代中重新排列锚点时，方向也会被更新。

为了实现个性化，我们尽量减少锚和重建损失的组合，即总损失函数如下：

$L=L_{anc}+L_{rec}$

其中重构损失 $L_{rec}$ 使合成的 $G(w_n)$ 与相应的输入图像 $I_{n}$ 之间的误差最小。这点与 MyStyle 里的重构损失是一样的，都是使用了 IPIPS 损失和 L2 损失的结合作为重构损失。

优化过程中，锚点对应的潜码和生成器的权值都被更新。除了使生成器适应输入图像集之外，重建损失在避免锚点损失的简单解决方案方面起着关键作用，例如，将所有锚点压缩到一个点。

一旦进行了优化，我们就得到了一个有组织的潜在空间 $W^{*}$ 和调整过的发生器 $G^{*}$ 。所有属性都可以在组织潜在空间中的 $m$ 维超立方体中进行控制。这个超立方体的边界可以简单地通过将所有锚点投射到超立方体 $d_m$ 的每个轴上并计算最小值和最大值来找到。 注意，在优化期间不使用的所有其他属性都编码在剩余的 PCA 维中。

图 4：上述过程的总览
GAN 论文阅读笔记（6）,GANNNNNN！！！,生成对抗网络,论文阅读,笔记

图 4 展示了这种可控个性化方法的运行过程概览。上半部分为训练过程，即将一个预训练的 StyleGAN 模型进行可控个性化的过程。给定一组具有相应属性的个人输入图像，我们首先将其编码到 StyleGAN 的 W 空间 ( 即预训练数据集潜空间 ) 中，以获得一组锚点，用圆圈表示。注意，颜色表示图像的属性。在本例中，不同的视图用黄色、橙色和红色表示，而不同的表达式用绿色和蓝色表示。然后，我们最小化一个由锚点 $L_{anc}$ 和重构损失 $L_{rec}$ 组成的目标函数，通过更新锚点来组织潜在空间，同时调整生成器。优化后，我们得到一个有组织的潜在空间 $W^{*}$ ，可以很容易地根据一组属性进行采样，以及一个调谐的生成器 $G^{*}$ ，可以产生保留了目标个体面部特征的图像。

3.2：用于图像生成、编辑与增强

3.2.1 ：图像生成、合成

过确保采样的潜码投射到 m 维超立方体中的所需位置，可以轻松地控制合成图像。但是，必须特别注意确保潜在代码不会落在个性化空间之外。

图像生成、合成的过程前半部分与 MyStyle 基本是相同的。

将锚点 $w^{*}$ 所围成的凸包定义为 $w^{*}$ 的个性化子空间。该凸包通过广义重心坐标表示为锚点的加权和，其中权重 ( 坐标 ) $\alpha=\{ \alpha_{n}\}^{N}_{n=1}$ 之和为 1 ，且大于 $-\beta$ ( $\beta >0$ ) 。这些概念的详解可以在 MyStyle 中找到。

作者在 MyStyle 之上提出了一种简单的改进策略：在膨胀凸包中进行控制采样。

具体来说，首先随机采样 α，以确保潜码在个性化子空间内。然后，我们将采样的潜码投影到PCA 中，并将投影值沿属性方向 $d_{m}$ 设置为所需值。

3.2.2 ：图像编辑 ( 语义编辑 )

由于属性是解纠缠了的，所以可以进行直接的语义编辑：将图像的潜码投影到 PCA 中，并通过更改超立方体中的坐标来执行编辑。

为了编辑图像 I ，先将图像投影到 $\alpha$ -空间：

$\alpha^{*}=\arg \min_{\alpha}L_{rec}(G(W^{*}\alpha),I)$
其中 $W^{*}$ 为一个沿其列有组织的锚点组成的矩阵。( 参考 MyStyle 中相关理论来理解，这一部分是一摸一样的) 一旦我们获得了优化的潜在代码，我们进一步调整生成器以更好地匹配输入图像。然后，通过更改 PCA 中的潜码来执行语义编辑。

3.2.3 ：图像增强

给定一个已知退化函数 Q 的输入图像 I ，我们的目标是增强图像，同时控制重建图像的属性。可以通过优化重构损失来做到这一点：

$\alpha^{*}=\arg \min_{\alpha}L_{rec}(Q(G(W^{*}\alpha)),I)+\lambda\sum_{m=1}^{M}||(W^{*}\alpha)\cdot d_{m}-\alpha_{m}||$

其中 $\lambda$ 为控制两项间平衡的超参数。式中第一项为重构损失：确保在应用退化函数后生成的图像与输入图像相似；第二项则鼓励潜在码 $W^{*}\alpha$ 在第 $m$ 个属性方向上的投影与期望值 $a_m$ 相似。如果想要控制增强的方向可以通过控制属性的一个子集来执行增强，而如果想要不受控制的增强，只需要去掉上式的第二项就可以了。