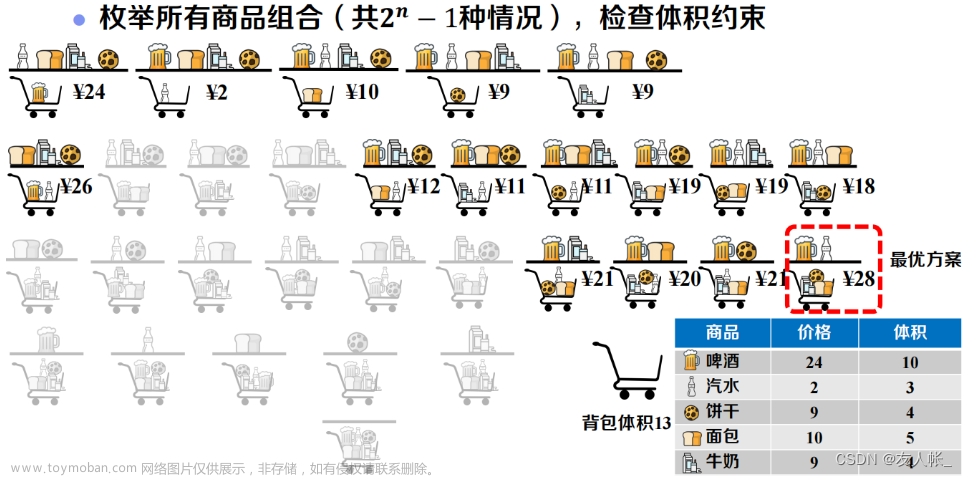
01背包问题(二维数组和滚动数组)
本题力扣上没有原题,大家可以去卡码网第46题 (opens new window)去练习,题意是一样的。
《代码随想录》算法视频公开课 (opens new window):带你学透0-1背包问题! (opens new window),相信结合视频再看本篇题解,更有助于大家对本题的理解。
这周我们正式开始讲解背包问题!
背包问题的经典资料当然是:背包九讲。在公众号「代码随想录」后台回复:背包九讲,就可以获得背包九讲的pdf。
但说实话,背包九讲对于小白来说确实不太友好,看起来还是有点费劲的,而且都是伪代码理解起来也吃力。
对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包。
看到题目的第一想法
装入背包的最大价值
维度
重量:weight
价值:value
背包容量:j
物品数量:i
看到代码随想录之后的想法(二维数组)
1 dp数组的定义和下标的含义
dp[i][j] 物品0~i之间能填入背包j的最大价值
2 确定递推公式
对于物品i 我们只有两种选择
1 若选择物品i 则最大值为 dp[i-1][j-weight[i]]+value[i]
2 若不选择物品i 则最大值为选择上一个物品的最大值 dp[i-1][j]
dp[i][j] =Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
3 dp数组初始化
由于需要 i-1 的值 则需要把第一行初始化:
当j<weight[i] dp[0][j]=0
当j>=weight[i] dp[0][j]=weight[i]
4 确定遍历顺序
先物品后背包
先背包后物品 都可以
5 举例推导dp数组
自己实现过程中遇到的困难(二维数组)
1 确定dp[i][j]时,若weight[i]>j 则没法取第二种情况,直接取第一种情况dp[i-1][j]
2 行列需要确认好,最好画图
看到代码随想录之后的想法(滚动数组)
将二维数组压缩成一维数组,只看一维数组中的内容
当选择新的物品时,一维数组中的内容,是上一层一维数组中的所有结果
1 dp数组的定义和下标的含义
dp[j] 物品0~i之间能填入背包j的最大价值
2 确定递推公式
对于物品i 我们只有两种选择
1 若选择物品i 则最大值为 dp[j-weight[i]]+value[i]
2 若不选择物品i 则最大值为选择上一个物品的最大值 dp[j]
dp[i][j] =Math.max(dp[j],dp[j-weight[i]]+value[i]);
3 dp数组初始化
只有一行,全为0
4 确定遍历顺序
只能先物品后背包
因为最新一行只能取上一行的内容来确认,要确保每一行都处理完
且只能从后往前遍历:如果从前往后,会把之前的数据打乱,而后续的数据需要依赖前面的数据
5 举例推导dp数组
自己实现过程中遇到的困难(滚动数组)
1 确定dp[j]时,若weight[i]>j 则没法取第二种情况,直接取第一种情况
2 行列需要确认文章来源:https://www.toymoban.com/news/detail-802421.html
import java.util.*;
public class Main {
//卡哥做法:一维数组
//1 确认dp数组,以及dp数组下标的含义
// dp数组 一维数组 dp[j]
// 相当于讲二维数组进行一个压缩,每次只取最后一行(第i层)
// 一维数组都是利用上一层的结果推出第i层的值
// 下标的含义 任意取物品0~i可存入空间为j的背包的最大值
//2 确定递推公式
// 对于物品i 有两种选择 取两者中的最大值
// 1 取物品i: 则当前i j 的value 为 dp[i-1][j-weight[i]]+value[i]
// 一维数组: dp[j]=dp[j-weight[i]]+value[i]
// 2 不取物品i:则当前 i j 的value 为dp[i-1][j];
// 一维数组: dp[j]=dp[j]
// 若weight[i]>j 则没法取第一种情况,直接取第二种情况
// Math.max(dp[j],dp[j]-weight[j]);
//3 dp数组如何初始化
// dp[j] 的值来自 dp[j] dp[j-weight[i]]
// 若初始化,不能让dp[j]过大,所以统一为最小非负数0
//4 确定遍历顺序
//从后往前,因为j-weight[i] 是需要获取这一行前面的值
//若从前往后,则会打乱上一层留下来的值 无法获取正确的j-weight[i]值
// 按行列都可以
//5 举例推导dp数组
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int size = sc.nextInt();
int[] value = new int[M];
int[] weight = new int[M];
for(int i = 0; i < M;i++) {
weight[i] = sc.nextInt();
}
for(int i = 0; i < M;i++) {
value[i] = sc.nextInt();
}
int[] dp = new int[size+1];
// 若比weight小则为0 若比weight大则为value
for(int i=0;i<=size;i++){
dp[i]=0;
}
//从i=0开始 也就是第0行就开始赋值
for(int i=0;i<weight.length;i++){
for(int j=size;j>0;j--){
// 这里要加上等于
if(j>=weight[i]){
dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i]);
}else{
dp[j]=dp[j];
}
}
}
System.out.println(dp[size]);
}
/* public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int size = sc.nextInt();
int[] value = new int[M];
int[] weight = new int[M];
for(int i = 0; i < M;i++) {
weight[i] = sc.nextInt();
}
for(int i = 0; i < M;i++) {
value[i] = sc.nextInt();
}
int[][] dp = new int[weight.length][size+1];
for(int i=0;i<weight.length;i++){
dp[i][0]=0;
}
// 若比weight小则为0 若比weight大则为value
for(int i=0;i<=size;i++){
if(i<weight[0]){
dp[0][i]=0;
}else{
dp[0][i]=value[0];
}
}
for(int i=1;i<weight.length;i++){
for(int j=1;j<=size;j++){
// 这里要加上等于
if(j>=weight[i]){
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}else{
dp[i][j]=dp[i-1][j];
}
}
}
System.out.println(dp[weight.length-1][size]);
}*/
}
/*
// weight 空间,value代表价值,size 代表行李空间
public static int bagProblem(int[] weight,int[] value,int size){
//卡哥做法:
//1 确认dp数组,以及dp数组下标的含义
// dp数组 二维数组 dp[i][j]
// 下标的含义 任意取物品0~i可存入空间为j的背包的最大值
//2 确定递推公式
// 对于物品i 有两种选择 取两者中的最大值
// 1 取物品i: 则当前i j 的value 为 dp[i-1][j-weight[i]]+value[i]
// 2 不取物品i:则当前 i j 的value 为dp[i-1][j];
// 若weight[i]>j 则没法取第一种情况,直接取第二种情况
//3 dp数组如何初始化
// dp[i][j] 的值来自 dp[i-1][j] dp[i-1][j-weight[i]]
// 则第一列和第一行需要有值
// 第一列的值都为0 因为j为0
// 第一行的值是物品0的值,当weight<j时 都为0 当weight>=j时都为物品0的weight
//4 确定遍历顺序
// 按行列都可以
//5 举例推导dp数组
int[][] dp = new int[weight.length][size+1];
for(int i=0;i<weight.length;i++){
dp[i][0]=0;
}
// 若比weight小则为0 若比weight大则为value
for(int i=0;i<=size;i++){
if(i<weight[0]){
dp[0][i]=0;
}else{
dp[0][i]=value[0];
}
}
for(int i=1;i<weight.length;i++){
for(int j=1;j<=size;j++){
if(j>weight[i]){
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
}else{
dp[i][j]=dp[i-1][j];
}
}
}
return dp[weight.length-1][size];
}
}*/
/*import java.util.*;
public class Main {
public static void main(String[] args) {
// 背包容量 N
// 物品种类 M
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int N = sc.nextInt();
int[] values = new int[M];
int[] weights = new int[M];
for(int i = 0; i < M;i++) {
weights[i] = sc.nextInt();
}
for(int i = 0; i < M;i++) {
values[i] = sc.nextInt();
}
int[][] dp = new int[M][N+1];
// 初始化
for(int i = weights[0]; i <= N; i++) {
dp[0][i] = values[0];
}
// 先物品
for(int i = 1; i < M; i++) {
// 后背包
for(int j = 0; j <= N; j++) {
if(weights[i] > j) {
dp[i][j] = dp[i-1][j];
} else {
dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weights[i]] + values[i]);
}
}
}
System.out.println(dp[M-1][N]);
}
}*/分割等和子集
力扣题目链接(opens new window)
题目难易:中等
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200
示例 1:
- 输入: [1, 5, 11, 5]
- 输出: true
- 解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
- 输入: [1, 2, 3, 5]
- 输出: false
- 解释: 数组不能分割成两个元素和相等的子集.
看到题目的第一想法
卡哥说可以用背包,但是我没想到
看到代码随想录之后的想法(二维数组)
其实题意就是这个数组能否拆分成总的sum的一半
若总和无法到达一半 ,则无法凑成
若总和可以拆分,题意为:0~i的物品填入sum/2的背包能否填满
1 dp数组的定义和下标的含义
dp[j] 物品0~i之间能填入背包j的最大价值
背包大小sum/2
2 确定递推公式
dp[j] =Math.max(dp[j],dp[j-weight[i]]+value[i]);
weight[i] 和 value[i] 都为nums[i]
3 dp数组初始化
都为0
4 确定遍历顺序
先物品后背包
且从后往前
5 举例推导dp数组
自己实现过程中遇到的困难(二维数组)
1 确定dp[i][j]时,若weight[i]>j 则没法取第二种情况,直接取第一种情况dp[i-1][j]
2 行列需要确认
3 看dp[sum/2] 是否==sum/2文章来源地址https://www.toymoban.com/news/detail-802421.html
class Solution {
public boolean canPartition(int[] nums) {
//背包问题:背包存放的最大价值,看是否选中该物品,在目标背包大小中取最大值
//该问题:背包存放的最大价值,在当前背包大小为target时,看最大价值是否能填满这个target
//两个子集的元素和相等
//其实就是求整个数组的和的一半,看数组中的值能否达到
//转换成背包问题,一个背包 大小为为nums总和的一半,如何相加才能填满
//dp数组下标的含义
//dp数组
//背包的重量 nums
//背包的价值 nums
//不可重复放入
// 确定dp数组的定义和每个下标的含义
// dp[] 为0~i下标填入背包空间j的最大价值,看是否等于11
// 确定递推公式
// dp[j] = max(dp[j],dp[j-nums[i]]+nums[i])
// 确定遍历顺序
// 从后往前
// dp数组初始化
// 都为0
// 手动推导dp数组
int sum = 0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
}
if(nums.length==1){
return false;
}
if(sum%2==1){
return false;
}
int target = sum/2;
int[] dp = new int[target+1];
//i为物品
//j为空间
for(int i=0;i<nums.length;i++){
for(int j=target;j>=nums[i];j--){
dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
//若这个位置的dp[j]可以填满
if(dp[j]==target){
return true;
}
}
}
return false;
}
}到了这里,关于动态规划day04(01背包问题)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!