【题目描述】
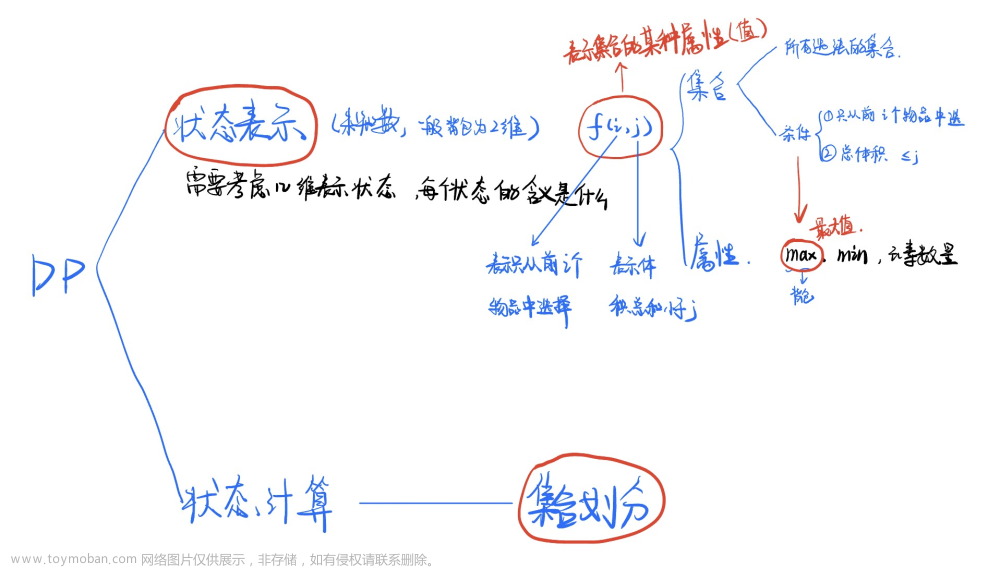
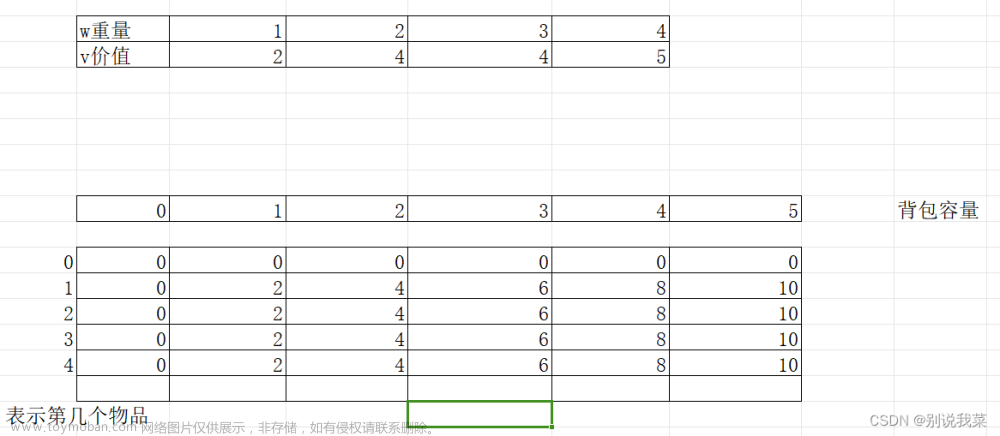
设有n�种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为M�,今从n�种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于M�,而价值的和为最大。
【输入】
第一行:两个整数,M�(背包容量,M≤200�≤200)和N�(物品数量,N≤30�≤30);第22..N+1�+1行:每行二个整数Wi��,Ci��,表示每个物品的重量和价值。文章来源:https://www.toymoban.com/news/detail-802658.html
【输出】
仅一行,一个数,表示最大总价值。文章来源地址https://www.toymoban.com/news/detail-802658.html
【输入样例】
10 4
2 1
3 3
4 5
7 9
【输出样例】
max=12
#include<bits/stdc++.h>
using namespace std;
int W,n;
int w[35],v[35];
int dp[205];
int main()
{
cin>>W>>n;
int i,j,k;
for(i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
for(i=1;i<=n;i++)
{
for(j=W;j>=w[i];j--)
{
for(k=1;k<=j/w[i];k++)
{
dp[j]=max(dp[j],dp[j-k*w[i]]+k*v[i]);
}
}
}
cout<<"max="<<dp[W];
return 0;
}到了这里,关于背包~~~~~~~~~3478:【例86.3】 完全背包问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!