最小生成树（详解普里姆算法）-Toy模板网

这篇具有很好参考价值的文章主要介绍了最小生成树（详解普里姆算法）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

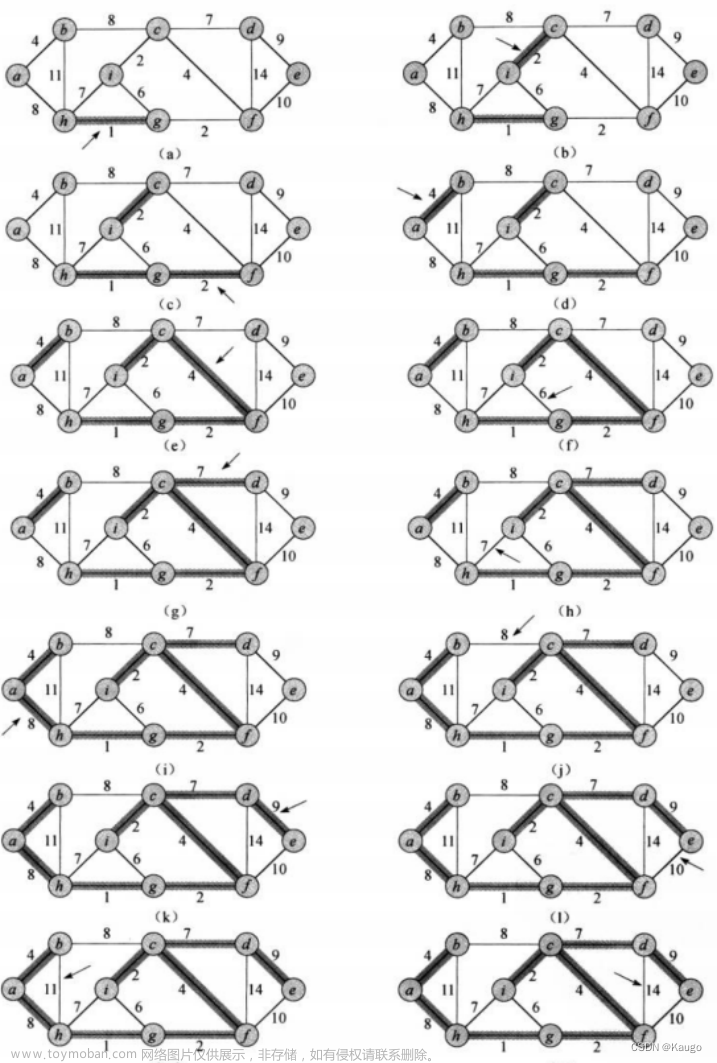
首先，我们来看一下图的一些基本知识点：

图：图 G=(V,E) 由顶点集 V 和边集 E 组成。每条边对应一个点对 (v,w)，其中 v，w 属于 V 。如果图中的点对是有序的，那么该图就是有向图，反之为无向图。

邻接点：若顶点 v 与 w 之间存在一条边，则认为顶点 v 与 w 邻接。

权：图中的每条边都可以对应一个数值，这种与边相关的数值称为权。

路径：在图 G 中，顶点 v1 到 vk 的路径是一个顶点序列 v1,v2,···,vk。

连通图：在无向图 G 中，若两个顶点之间存在路径，则认为这两个顶点是连通的。如果在无向图 G 中,任意两个顶点都是连通的，则称 G 是连通图。

完全图：若图中任意两个顶点之间都存在一条边，则该图为完全图。

稀疏图和稠密图：当图中边的数量比较少时，称该图为稀疏图；而当图接近完全图时，称该图为稠密图。

生成树：一个连通图的生成树是一个极小连通子图，它含有图的全部顶点，但只有足以构成一棵树的 n-1 条边。

最小生成树：对于边上带有权值的图，在图的所有生成树中，树的权值最小的生成树称为最小生成树。

接下来我们进入正题，来看看如何用普里姆算法实现最小生成树。

普里姆算法的思想：

普里姆算法的初始状态仅有一个顶点在最小生成树的顶点集合 U 中，其他顶点都在另一个由不在最小生成树上的顶点构成的集合 V 中。在后续的每一步中，通过选择所有连接最小生成树上的顶点 u 和不在树上的顶点 v 之间的边中权值最小的边 (u,v) ，将对应的顶点 v 拉入最小生成树的顶点集合中。当图中所有的顶点都已加入到树中，算法运算结束后，此时得到的 n 个顶点和 n-1 条边就构成了一棵最小生成树。

普里姆算法最小生成树,算法思考,数据结构,算法,图论,数据结构,c++

实现方法：

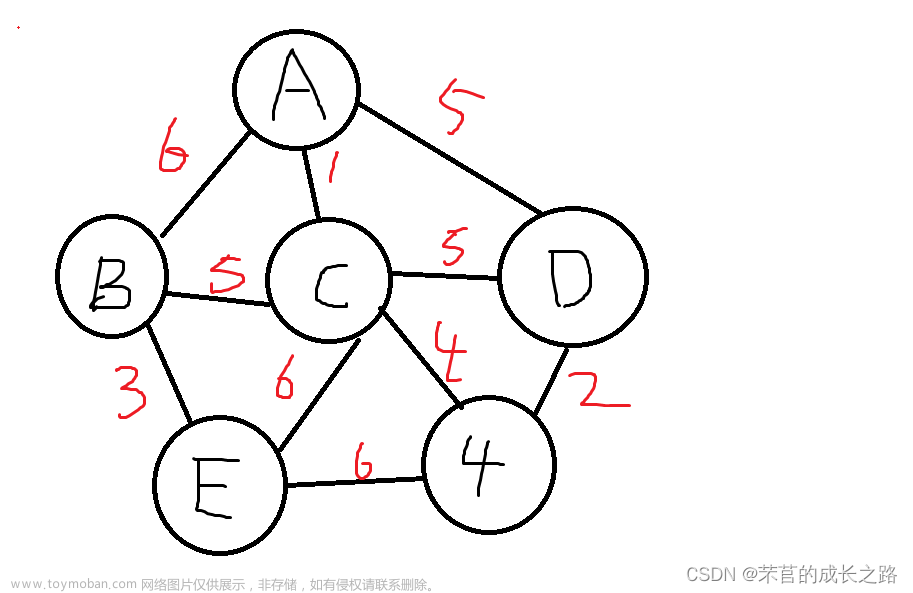
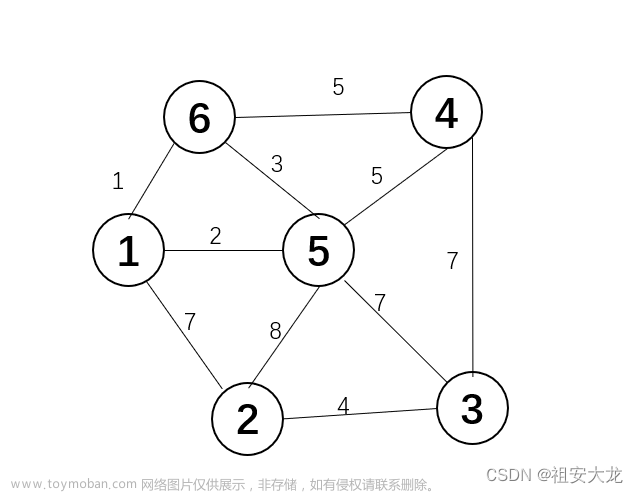
以上方无向有权图为例。我们创建三个数组 Adjvex[]，Lowcost[]，Flag[]。Adjvex[]表示权值最小的边 (u,v)中位于最小生成树中的顶点； Lowcost[]保存不在最小生成树中的各点到最小生成树中的点的边的最小权值（初始化为无限大）； Flag[]标注点是否已加入最小生成树中（初始化为0）。用图表示过程如下：

1、初始状态，我们从 1 号点出发，将1加入树中，Flag[1] 置为1。然后我们遍历点 1 的所有邻接点，把相应权值填入Lowcost中，这里点 1 到点 1 的权值我们视为0。如图：

编号	1	2	3	4	5
Adjvex	1	1	1	1	1
Lowcost	0	5	6	3
Flag	1	0	0	0	0

2、我们从 Lowcost 中选出权值最小的边对应的点（该点不在树中，即Flag对应为0），这里为点4，将其加入树中，Flag[4]置为1。

编号	1	2	3	4	5
Adjvex	1	1	1	1	1
Lowcost	0	5	6	3
Flag	1	0	0	1	0

3、接着遍历点 4 的所有邻接点，与原来的权值作比较，把较小的权值填入Lowcost 中，若新的权值取代了旧的权值，还要同时改变 Adjvex 的值为 4。

编号	1	2	3	4	5
Adjvex	1	1	4	1	4
Lowcost	0	5	2	3	7
Flag	1	0	0	1	0

4、重复2、3步，直到所有的点均已加入最小生成树中。此时 Lowcost 行的和即为最小生成树的值，最终表格如下，最小生成树的值=1+2+3+4=10。

编号	1	2	3	4	5
Adjvex	1	5	4	1	3
Lowcost	0	1	2	3	4
Flag	1	1	1	1	1

程序代码：

# include <iostream>
# define SIZE 20
# define NEWSIZE 20
# define maxn 100000000   //表示无限大
using namespace std;
typedef struct ArcNode {  //边的结点结构类型
	int adjvex;           //该边的终点编号
	int weight;           //该边的权值
	struct ArcNode* nextarc;  //指向下一条边的指针
}ArcNode;
typedef struct VexNode {  //顶点结构
	char data;
	ArcNode* firstarc;    //指向第一条与该顶点有关的边的指针
}VexNode;
typedef struct Graph {    //邻接表结构类型
	VexNode* VNode;       //定义邻接表
	int vexnum, arcnum;   //顶点数和边的个数
	int size;             //邻接表的大小
}Graph;

int* Adjvex;  //保存在最小生成树中的顶点
int* Lowcost; //保存不在最小生成树中的各点到最小生成树中的点的边的最小权值 
int* Flag;    //标注该点是否已加入最小生成树

void Create_Graph(Graph& G)   //创建图（邻接表）
{
	cout << "顶点的个数:";
	cin >> G.vexnum;
	G.VNode = (VexNode*)malloc(SIZE * sizeof(VexNode));
	G.size = SIZE;
	while (G.size <= G.vexnum) {   //根据点的个数动态分配空间
		G.VNode = (VexNode*)realloc(G.VNode, (G.size + NEWSIZE) * sizeof(VexNode));
		G.size += NEWSIZE;
	}
	Adjvex = (int*)malloc((G.size + 10) * sizeof(int));
	Lowcost = (int*)malloc((G.size + 10) * sizeof(int));
	Flag = (int*)malloc((G.size + 10) * sizeof(int));
	cout << "请输入各顶点的名称:";
	for (int i = 1; i <= G.vexnum; i++) {
		cin >> G.VNode[i].data;
		G.VNode[i].firstarc = NULL;  //邻接表初始化，所有单向链表均为空表
	}
	cout << "请输入边的个数:";
	cin >> G.arcnum;
	cout << "请输入各边起点和终点的编号及权重：" << endl;
	int x, y, w;    //x:起始点，y:终点，w:权重
	ArcNode* p, * q;
	for (int i = 1; i <= G.arcnum; i++) {
		cin >> x >> y >> w;
		p = (ArcNode*)malloc(sizeof(ArcNode)); //创建一个用于存放当前边的结点p
		p->nextarc = NULL;
		p->adjvex = y;
		p->weight = w;
		q = G.VNode[x].firstarc;
		//将边按顺序插入到链表末尾
		if (q == NULL) {
			G.VNode[x].firstarc = p;
		}
		else {
			while (q->nextarc != NULL) {
				q = q->nextarc;
			}
			q->nextarc = p;
		}
		p = (ArcNode*)malloc(sizeof(ArcNode));
		p->nextarc = NULL;
		p->adjvex = x;
		p->weight = w;
		q = G.VNode[y].firstarc;
		if (q == NULL) {
			G.VNode[y].firstarc = p;
		}
		else {
			while (q->nextarc != NULL) {
				q = q->nextarc;
			}
			q->nextarc = p;
		}
	}
}

void MinSpanningTree_Prim(Graph& G, int v) //从顶点v出发求图的最小生成树
{
	for (int i = 1; i <= G.vexnum; i++) {  //初始化
		Adjvex[i] = v;
		Lowcost[i] = maxn;
		Flag[i] = 0;
	}
	Lowcost[v] = 0;          //初始点对应的权置为0
	Flag[v] = 1;             //标记初始点（即将初始点加入树中）
	cout << G.VNode[v].data; //输出初始点的值
	int num = 1;             //记录目前最小生成树中的点的数目
	ArcNode* p;
	while (num < G.vexnum) {
		p = G.VNode[v].firstarc; //p为新加入树的点的第一个邻接点
		while (p != NULL) {      //由于新点加入，更新各不在最小生成树中的点到最小生成树中点的最小距离
			if (!Flag[p->adjvex] && Lowcost[p->adjvex] > p->weight) {
				Lowcost[p->adjvex] = p->weight;
				Adjvex[p->adjvex] = v;
			}
			p = p->nextarc;
		}
		int min = maxn;
		for (int i = 1; i <= G.vexnum; i++) {  //寻找目前到最小生成树距离最小的点（该点不在最小生成树中）
			if (!Flag[i] && Lowcost[i] < min) {
				min = Lowcost[i];
				v = i;               //更新v为目前到最小生成树距离最小的点（该点不在最小生成树中）
			}
		}
		Flag[v] = 1;             //标记该点（即将该点加入最小生成树中）
		cout << G.VNode[v].data; //输出新加入树的点的值
		num++;                   //最小生成树中的点的数目+1
	}
}

int main()
{
	Graph G;
	Create_Graph(G);
	int sum = 0;
	cout << "最小生成树为:";
	MinSpanningTree_Prim(G, 1);  //从1号点出发
	cout << endl;
	for (int i = 1; i <= G.vexnum; i++) {
		cout << Adjvex[i] << " ";
	}
	cout << endl;
	for (int i = 1; i <= G.vexnum; i++) {
		cout << Lowcost[i] << " ";
		sum += Lowcost[i];         //求最小生成树的值
	}
	cout << endl;
	for (int i = 1; i <= G.vexnum; i++) {
		cout << Flag[i] << " ";
	}
	cout << endl;
	cout << "最小生成树的值为:" << sum << endl;
	return 0;
}

运行结果：

顶点的个数:5
请输入各顶点的名称:A B C D E
请输入边的个数:7
请输入各边起点和终点的编号及权重：
1 2 5
1 3 6
1 4 3
2 5 1
3 4 2
3 5 4
4 5 7
最小生成树为:ADCEB
1 5 4 1 3
0 1 2 3 4
1 1 1 1 1
最小生成树的值为:10

总结：普里姆算法的核心部分是一个双重循环。第一层循环是对所有的顶点；第二层有两个循环，一个是遍历邻接点更新数组，另一个是寻找 Lowcost 中的最小值。因此，普里姆算法的时间复杂度是O(n^2)。

以上是我的学习成果，很高兴与大家分享。文章来源地址https://www.toymoban.com/news/detail-803025.html

到了这里，关于最小生成树（详解普里姆算法）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！