【算法与数据结构】416、LeetCode分割等和子集-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法与数据结构】416、LeetCode分割等和子集。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

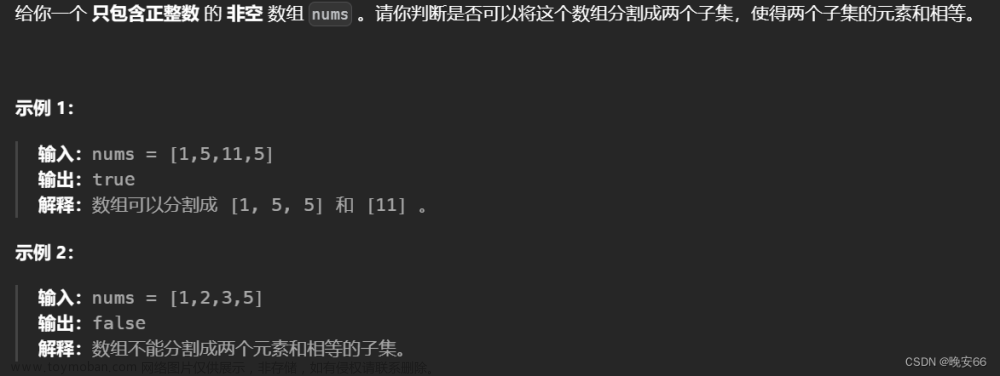
【算法与数据结构】416、LeetCode分割等和子集,算法,算法

二、解法

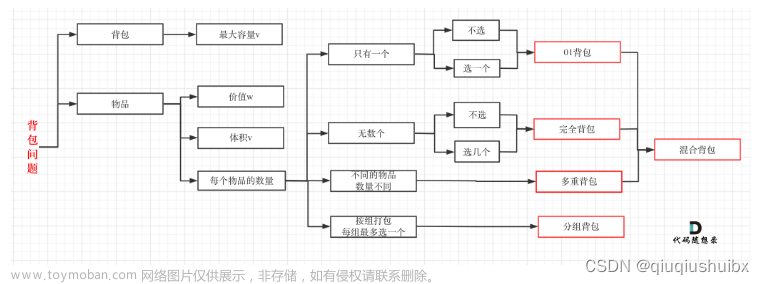
思路分析：本题可以抽象成一个01背包的问题，关于01背包可以看【算法与数据结构】算法与数据结构知识点。本题只需要求出数组的累积和，然后和的一半就可以视为背包的最大重量，目标就是要判断数组中是否有和为背包最大重量的子集。其中，物品重量和价值相同，就是数组元素的值。根据01背包的思想，我们写出如下一维滚动数组的代码。
程序如下：

class Solution {
public:
	bool canPartition(vector<int>& nums) {
		int sum = 0;
		for (int i : nums) sum += i;	// 也可以用accumalte函数
		if (sum % 2 != 0 || nums.size() < 2) return false;
		vector<int> dp(sum/2 + 1, 0);
		for (int i = 0; i < nums.size(); i++) {
			for (int j = sum / 2; j >= nums[i]; j--) {
				dp[j] = max(dp[j], dp[j - nums[i] ] + nums[i]);
			}
		}
		if (dp[sum / 2] == sum / 2) return true;
		return false;
	}
};

复杂度分析：

时间复杂度： $O(n^2)$ 。
空间复杂度： $O (n)$ 。

三、完整代码

# include <iostream>
# include <vector>
# include <numeric>
# include <algorithm>
using namespace std;

class Solution {
public:
	bool canPartition(vector<int>& nums) {
		int sum = 0;
		for (int i : nums) sum += i;	// 也可以用accumalte函数
		if (sum % 2 != 0 || nums.size() < 2) return false;
		vector<int> dp(sum/2 + 1, 0);
		for (int i = 0; i < nums.size(); i++) {
			for (int j = sum / 2; j >= nums[i]; j--) {
				dp[j] = max(dp[j], dp[j - nums[i] ] + nums[i]);
			}
		}
		if (dp[sum / 2] == sum / 2) return true;
		return false;
	}
};

int main() {
	vector<int> nums = { 1,5,11,5 };
	Solution s1;
	bool result = s1.canPartition(nums);
	cout << result << endl;
	system("pause");
	return 0;
}