前言:本科学了四年机械,后面转头去了电子信息读研,以FPGA的脉压入手,在从零开始的路上CSDN对我的帮助很大,现整理所学,与诸君共勉。本文不少代码均是参考CSDN上的前辈们一步一步理解做出来的,如有冒犯之处,烦请谅解。
目录
一:脉冲压缩原理介绍
1.我们简单了解一下脉冲压缩到底是什么?
2.我们再来了解一下我们所使用的线性调频信号
二.基于matlab的脉冲压缩仿真
1.脉冲压缩信号生成
2.DDC数字下变频
3.匹配滤波
4.加窗处理
5.杂波抑制和多目标测距
三.Vivado实现
一:脉冲压缩原理介绍
1.我们简单了解一下脉冲压缩到底是什么?
首先,一个好的雷达是能够准确探测足够远的两个足够近的目标。
在最早的时候,雷达脉冲宽度与带宽是呈反比的,在这个基础上,脉冲宽度决定了信号的最大探测距离,而脉冲带宽决定了距离的分别率,这就导致距离分辨力和最大探测距离出现了不可调和的矛盾。
我们通过这样两个对比图来看,早期雷达时宽带宽积为1之间带来的矛盾:
宽脉冲信号,信号能量足够,但是回波重叠

窄脉冲信号,回波不重叠,探测距离不够

(看到这里,其实能够看见探测距离和探测精度其实都是受到了时宽的影响,由于早期雷达带宽和时宽呈反比,才将二者联系起来,但是早期人们不知道雷达探测精度只与带宽有关,所以一直所说的探测精度同探测距离矛盾的问题一定要建立在早期雷达时宽和带宽呈反比的基础上。)
针对探测距离同精度的问题,随之就有学者提出了脉冲压缩技术的核心,即匹配滤波。我们在发射时仍然采取大时宽信号,而在接收时将信号压缩为窄信号,这样就解决了雷达这两个指标之间的矛盾。
我们通过如图来理解脉冲压缩,很形象和直观,在时域上:

这样一来多目标带来的回波就不至于互相重叠掩埋。
随着雷达的发展,人们渐渐发现了雷达探测精度只与带宽有关!

式子左边为距离分辨力,右边C为光速,可以看到带宽越大,距离分辨力越高。
并且随着发展,我们发现了许多大时宽带宽积信号,这种信号一出来,其实时宽和带宽一定程度没有那么大的矛盾了,而这个时候,脉冲压缩技术更多的使得信号达到它的最大理论分辨力,即上图公式。
当我发射一个大时宽信号时候,回波信号能被压缩为一个窄尖,理论上不超过上图公式所计算出的距离分辨力,都会在时域上分隔开,我们将在第二章通过matlab进行验证和更直观的说明。
在合成孔径雷达里也需要用到脉冲压缩,这里放一个我室友帮我跑的学校缩写,用来做文章封面。

文章来源地址https://www.toymoban.com/news/detail-804170.html
2.我们再来了解一下我们所使用的线性调频信号
我们直接上表达式:(这个式子比较简单,我们不做过多的赘述)
值得一提的是根据欧拉公式,该式子存在余弦和复数表达式,但是复数表达式经常存在实部和虚部的问题,我没学过复变,所以不是很懂,不过matlab上还是可以跑出来的


我们对相位求导,可以得到瞬时频率:

因此线性调频信号即瞬时频率随时间线性u增大的信号。
同时LFM也是大时宽带宽积信号,其时宽带宽积也等于脉冲压缩的压缩比
大概就先说这么多吧,之后的推导我们在matlab上接着推导。
二.基于matlab的脉冲压缩仿真
1.脉冲压缩信号生成
根据第一章的公式,我们简单模拟一个幅值为1的线性调频信号,其调频斜率与带宽B,时宽T有关
我们直接贴代码:
%% 线性调频信号生成
clc;
close all;
%LFM参数设置
B = 30e6; %带宽
T = 10e-6; %时宽
K = B/T; %调频斜率
Fs = 4*B; %采样频率
F0 = 150e6; %初始频率和中心频率
Ts = 1/Fs; %采样周期
N = ceil(T/Ts); %ceil函数是向上取整数,也常使用四舍五入的round函数
t = linspace(-T/2,T/2,N); %linspace函数可以在-T/2到T/2之间产生N个点(均分)
%产生调频信号
LFM1 = exp( 1j* pi * K * t.^2); %线性调频信号复数表达式(F0=0) .*是点乘运算
LFM2 = exp( 1j*(2 * pi * F0 * t + pi * K * t.^2)); %线性调频信号复数表达式
LFM3 = cos(pi * K * t.^2); %线性调频信号的余弦表达式(F0=0)
LFM4 = cos(2 * pi * F0 * t + pi * K * t.^2); %线性调频信号余弦表达式通过fft函数可以看到LFM的频域图像
%% 作图
figure(1)
%subplot(1,2,1) %生成三行两列个子图,现在激活第一个
plot(t*1e06,LFM1);
title('线性调频信号(复数表达式(F0=0))');
xlabel('时间(us)');
ylabel('幅度');
%xlim([-T/2,T/2]); %限制X轴上下限值
grid on;%添加网格
axis tight;
figure(2)
%subplot(1,2,2) %生成三行两列个子图,现在激活第二个
f = linspace(-Fs/2,Fs/2,N);
LFM1_FFT = fftshift(abs(fft(LFM1,N)));
%abs返回绝对值,直接对函数傅里叶变换,fftshift调整0频位置
plot(f*1e-6,LFM1_FFT);
title('线性调频信号(复数表达式(F0=0))频域图');
xlabel('频率(MHz)');
ylabel('幅值');
grid on;%添加网格
axis tight;
%F0=5e6
figure(3)
%subplot(1,2,1) %生成三行两列个子图,现在激活第一个
plot(t*1e6,LFM2);
title('线性调频信号(F0=150HMz)')
xlabel('时间(us)');
ylabel('幅度');
%xlim([-T/2,T/2]); %限制X轴上下限值
grid on;%添加网格
axis tight;
figure(4)
%subplot(1,2,2) %生成三行两列个子图,现在激活第二个
LFM2_FFT = fftshift(abs(fft(LFM2,N)));
plot(f*1e-6,LFM2_FFT);
title('线性调频信号(F0=150HMz)频域图')
xlabel('频率(MHz)');
ylabel('幅值');
grid on;%添加网格
axis tight;150MHz的中频图像过于密集不太好看,我放两张0频的以供参考。


线性调频信号的生成就到这里
2.DDC数字下变频
一般来说,我们发射的信号为了具有更大的能量和抗干扰,穿透力等,都会搭载高频信号,但是回来的高频信号需要倍频采样,这就会导致采样频率过高,所以我们通过DDC数字下变频的方式将信号降到低频。
主要有三个步骤:正交调制、低通滤波、抽取。
可以简单讲一下正交调制的原理,首先输入的信号经过采样到了处理中心,这时候NCO(我也不知道是啥)会产生所需的两组正交本振信号(根据发射信号公式可以推出):

大概可以看清楚吧?将采样数据与正交本振信号相乘(混频)之后通过三角函数积化和差公式分解后,我们可以得到高频和低频两部分:
这里就输出了I、Q两路信号,根据公式可以看到高频f0被分出到了式子的右边。

再通过低通滤波处理,设置截止频率,输出后的信号:

至于抽取倍频,其实就是通过“跨步读取”的方式进一步降低频率,这个比较简单,就不说了。
接下来,我们通过Matlab进行实操:
我们的正交处理要比上诉简单很多,走了一个捷径
交处理部分中最关键的是如何产生本振信号,在FPGA实际处理的过程中,我们可以调用Vivado中DDC IP核来产生;此外也可以根据f0和TS来计算出对应的两组正交值。我们这里采用第三种最简单的方法:(因为打字时候公式不太好弄,我直接放图片了)

我们在参数设计中预先将中心频率 设为150Mhz;采样频率
设为150Mhz;采样频率 设置为四倍带宽(即:120MHz)满足第三章正交处理要求。我这里把DDC这一步另存为一个函数方便调用,代码一起放上来:
设置为四倍带宽(即:120MHz)满足第三章正交处理要求。我这里把DDC这一步另存为一个函数方便调用,代码一起放上来:
function [ddc_i,ddc_q] = DDC(x)
%% DDC下变频输出
n = 1:length(x);
cos_unit = [1,0,-1,0];
cos_osc =cos_unit(mod(n,4)+1); % mod(b,a) 求余运算 ,b/a的余数.
sin_unit = [0,1,0,-1];
sin_osc =sin_unit(mod(n,4)+1);
DDC_out_i1 = x.*cos_osc;
DDC_out_q1 = x.*sin_osc;
DDC_out_i = filter(filter,DDC_out_i1);
DDC_out_q = filter(filter,DDC_out_q1);
%% 抽取,会降低分辨率
deciN = 2;
ddc_i = DDC_out_i(1:deciN:length(DDC_out_i));
ddc_q = DDC_out_q(1:deciN:length(DDC_out_q));
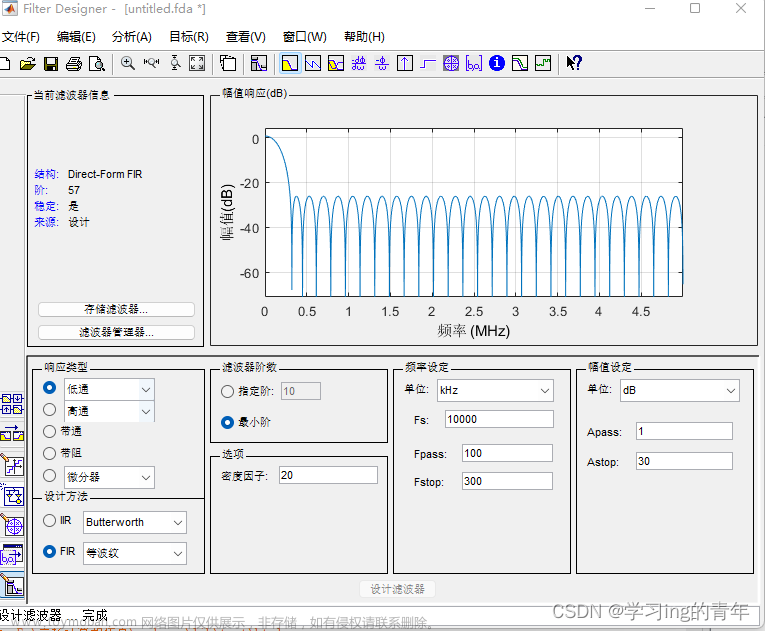
end前面就是正常的信号进入,到filter是我们的滤波器,在Matlab低通滤波这部分处理中,我们可以通过软件所自带的fdatool工具直接生成低频滤波器:首先在命令行窗口中输入fdatool,软件会生成出低通滤波器编辑器Filter Designer,我们调整滤波器参数采样频率为120MHz,低通截止频率为22MHz,通过频率为20MHz,完成参数设计后点击Designe,系统会生成出一个filter.m的工程文件

最后就是抽取倍频。直接放三个过程图
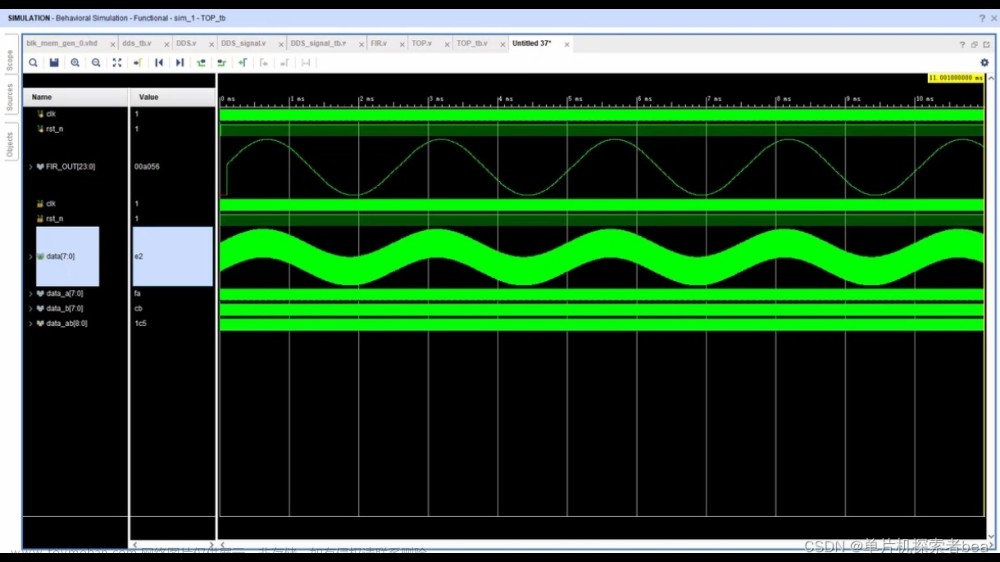
生成正交后图像:



简单说明一下,这个信号前面是因为我补了120个零点(1s),才会产生前面的直线。
3.匹配滤波
匹配滤波就是脉冲压缩的核心步骤了,前面我们只是讲了这一步是用来干什么,现在具体讲一下为什么,我就不做公式的推导了。
首先通俗一点,就是讲信号与其自相关函数进行时域卷积,其实就相对于1*1=1,100*100=10000(我是这样理解的),这样一下就把其加权放大了,达到了尖峰的效果,推荐再理解一下卷积
分享一篇文章:https://blog.csdn.net/bitcarmanlee/article/details/54729807
反正就是一个卷积处理,那么我们知道时域卷积等效于频域相乘,所以依据滤波器的不同进入时期我们会得到三个频域的处理方式。
首先看,时域卷积:
脉冲压缩在时域的处理方式主要是对线性调频信号与其自相关函数做卷积处理。所以第一步是构造自相关函数,我们已知原线性调频信号的参数与函数,对其在时域表达式进行反褶再取共轭后即可得到自相关函数,之后两者卷积,即可生成脉压后的信号。
自相关函数的构造,我们主要通过filplr函数和conj函数来实现。前者是进行反褶操作,简单来说也就是将1、2、3的序列或矩阵输出为3、2、1。而后者conj则是直接取共轭函数,两个函数依次套用即可生成自相关函数。
卷积运算是通过Matlab自带的快速卷积处理函数conv函数完成,需要注意的是卷积运算后信号的长度会发生改变,若第一个函数的长度为N1,第二个长度为N2,卷积后长度则为N1+N2-1。而我们这里两个函数长度一样,则输出长度为2N-1。我们可以得到仿真图,我们再将图像做归一化处理,同时导入sinc函数红点,可以发现在基带附近具有较高的拟合度,而sinc函数的傅里叶变换正好是幅值为1的矩形脉冲信号。
%% 时域匹配滤波
H_LFM1 = conj(fliplr(LFM1)); %conj是取共轭,fliplr是进行矩阵左右翻转
s1 = conv(LFM1,H_LFM1); %conv是将输入信号与匹配滤波信号卷积输出,
N1 = N+N-1 ;%线性卷积后信号长度变为 N1+N2-1
t1 = linspace( -T , T , N1); %信号长度变化%信号输出
figure(1);
subplot(2,1,1);
plot( t1*1e6 , abs(s1) );
xlabel('t /us'),ylabel('幅度谱');
title('时间反褶取共轭,时域卷积');
grid on;%添加网格
axis tight;
%归一化;辛克函数
Z=abs(s1);Z=Z/max(Z); Z=20*log10(Z+1e-6);
Z1=abs(sinc(B.*t1)); Z1=20*log10(Z1+1e-6);%辛克函数
subplot(2,1,2);
t1=t1*B;
plot(t1,Z,t1,Z1,'r.' );
xlabel('时间/s ');
ylabel('幅值/dB');
title('线性调频信号经过匹配滤波(归一化)');
axis([-15,15,-50,inf]);
grid on;%添加网格
频域处理:
频域的处理和时域类似,根据第二章推导的公式,可以大致分为三种处理顺序:
- 先构造出反褶,共轭的滤波函数,和信号一起补零之后进行FFT到频域,然后频域相乘。最后进行IFFT(FFT逆运算)进行频域到时域的逆运算。
- 信号补零进行FFT到频域之后,进行共轭得到滤波频域函数,相乘之后进行IFFT逆运算。
- 信号补零进行FFT到频域之后,直接在频域构造出匹配滤波器,相乘之后进行IFFT逆运算。
这三种操作顺序主要都是受自相关函数生成的影响,理想情况下第一种和第二种没有太大区别,但是比较麻烦也需要注意的是,前两种方法都中需要进行补零至选定长度的前置处理,由于不同滤波器弃置区不一样,且等于响应信号长度减一,所以为了进行有效的处理,FFT的点数最好是2的次方数且大于信号长度。具体原因是因为Matlab中FFT是做循环卷积运算,而匹配滤波需要的是线性卷积,所以需要在函数前补N-1个0,同时补零也可以提高分辨率。
(md,这个地方CSND鬼畜了,写的好好的突然没了退回到这一段,从这到这章完,写了三遍)
基于第一种顺序,我们首先对线性调频信号及其自相关函数做FFT离散快速傅里叶变换到频域,然后频域直接相乘得到脉冲压缩函数后进行IFFT逆变换回到时域后,同时也可以做归一化处理后和Sinc函数进行拟合。
%% 频域匹配滤波1 (复制发射脉冲进行时间反褶并取共轭,计算补零DFT)
N2 = 2*N-1; %循环卷积长度
t2 = linspace( -T , T , N2);
Hf2 = fft(H_LFM1,N2); %频域匹配滤波器
Sf2 = fft(LFM1,N2);%频域信号
S2 = Sf2 .* Hf2;%频域乘积
s2 = ifft(S2);figure(2);
subplot(2,1,1);
plot( t2*1e6 , abs(s2) )
xlabel('t /us');
ylabel('幅度谱');
title('时间反褶取共轭,补零FFT,频域乘积,IFFT');
grid on;%添加网格
subplot(2,1,2);
Z2=abs(s2);Z2=Z2/max(Z2); Z2=20*log10(Z2+1e-6);%归一化
t3 = t2*B;
plot(t3,Z2,t1,Z1,'r.');
axis([-15,15,-50,inf]);
xlabel('时间/s ');
ylabel('幅值/dB');
title('线性调频信号经过匹配滤波(归一化)');输出图像:基本上和时域处理没什么区别

4.加窗处理
由于脉冲压缩会不可避免的产生旁瓣,旁瓣按照1/X的幅值递减,但较大的旁瓣仍会淹没其他微弱的信号,导致目标无法分辨,所以为了提高性能指标,我们还会对脉压信号增加窗函数以改变波形。加窗主要是在时域上,对匹配滤波器进行点成乘运算,其目的是抑制旁瓣,常用的有:Hanning窗、Blackman窗、kaiser窗等,不同的窗效果不一样,如图是常用窗函数的性能表
| 窗函数 |
最高旁瓣(dB) |
归一化主瓣宽度(dB) |
最大信噪比损失(dB) |
| 矩形 |
-13 |
0.89 |
3.92 |
| Hanning |
-32 |
1.44 |
3.18 |
| Hamming |
-43 |
1.30 |
3.10 |
| Blackman |
-58 |
1.68 |
3.47 |
我们在仿真的过程中,选择汉明(Hamming)窗来抑制旁瓣;首先直接调用Matlab自带的汉明窗函数,再与信号的自相关函数相乘得到加权后的匹配滤波器系数。之后按照频域处理的方法得到加窗后的图像:
%% 加窗
w = hamming(N)';
H_w = H_LFM1.*w ; % 加窗
Hf3 = fft(H_w,N2); %频域匹配滤波器
S3 = Sf2 .* Hf3;%频域乘积
s3 = ifft(S3);figure(1)
subplot(2,1,2)
plot( t2*1e6 , abs(s3) )
xlabel('t /us');
ylabel('幅度谱');
title('时间反褶取共轭,补零FFT,频域乘积,IFFT(加窗)');
grid on;%添加网格
figure(2)
subplot(2,1,2)
Z3=abs(s3);Z3=Z3/max(Z3); Z3=20*log10(Z3+1e-6);%归一化
t3 = t2*B;
plot(t3,Z3);
axis([-100,100,-50,inf]);
xlabel('时间/s ');
ylabel('幅值/dB');
title('线性调频信号经过匹配滤波(归一化)(加窗)');
放到一个图可以明显对比出加窗的效果:

但需要注意的是,窗函数的引入实际上是对回波做了加权系数处理,虽然抑制了旁瓣,但同时也会导致主瓣展宽,降低了脉压后的幅值,造成了信噪比损失。简单来说就是以损失一定信号特性为代价,来提高主副比。
5.杂波抑制和多目标测距
通过现有的脉冲压缩模型,我们可以验证其作为最佳线性滤波器的杂波抑制效果
在现实情况中,雷达系统发射机发射出线性调频信号后,返还回来的目标信号除目标回波外还会夹带杂波噪声和干扰信号两部分。本节不考虑干扰信号带来的影响,通过添加高斯白噪声来模拟杂波信号的对回波的干扰,再通过匹配滤波器输出后,可以观察对杂波的抑制效果。
在matlab中仅需要使用awgn函数即可,通过Y = awgn(采样信号,信噪比);一行代码即可:
我们这里添加信噪比为1dB的杂波:

我们可以对比添加杂波前后的信号输出,可以明显看见线性调频信号已经掩埋在了杂波里。
将合成的回波Y直接导入到我们的模型里:通过建立好的模型,我们可以清晰的看见原本杂乱无章的波形如图,所示经过脉冲压缩后可以明显的看见信号回波所产被压缩成的尖峰,这就是自相关函数对于杂波来说是无序的,而对于发射的回波确是最匹配的。
为了更好的看到效果,我们再引入信号参数一致但未添加噪声的脉冲压缩信号输出,效果如图所示:可以看到大量杂波的引入使得回波信号杂乱无章,虽然输出的图像效果不如没有噪声的明显,但是尖峰仍然清晰可见,到达了在高噪声环境中输出的效果。

多目标测距:
多目标测距这部分重点参考代码,我就不放出来了,大家有兴趣可以找到很多,我仅做一个效果展示:首先根据参数确定距离分辨力,然后做一个对照组

| 雷达发射信号参数 |
参数值 |
目标距离 |
10km~15km |
| 幅值 |
1.0 |
目标一 |
10.5km |
| 信号波形 |
线性调频信号 |
目标二 |
11km |
| 频带宽度 |
30 (MHz) |
目标三 |
12km |
| 脉冲宽度 |
10(us) |
目标四 |
12km+10m |
| 中心频率 |
150(MHz) |
目标五 |
14km |
| 雷达接收方式 |
正交解调 |
目标六 |
14km+3m |
该测距任务中,我们分别围绕5 m的分辨率设置了10 m和3 m两个距离看线性调频信号的分辨效果。此外我们假定雷达截面积都为1,目标静止,取光速为30×108 m/s,根据最小10 km,最大15 km后光速的两段时间差来设置返回信号窗,建立好参数模型后带入我们的雷达仿真系统。
输出的结果如图所示,没有经过脉冲压缩的回波,目标之间波形相互干扰,无法得到目标的准确位置,而经过脉冲压缩后的信号在输出的图像上大概分为了四个尖峰,主要是由于第三与第四个目标,第五与第六个目标相距太近造成。

经过脉冲压缩处理后,我们放大目标三四,五六:


通过输出图像,可以发现目标回波的误差非常小。从理论上完成脉冲压缩在雷达测距任务上的功能,同时也验证了线性调频信号的分辨率的雷达方程。
三.Vivado实现
目前CSDN上主要都是姜文博学长的时域法,大家可以自行搜索学长的文章。很少看到用频域做的,频域我有师兄做了,我大概看明白了思路,不过还没自己做出来。我把思路流程发给大家以供参考:
时域:

频域:
 写的有点累了,就不想过多叙述了,最后就放一下多目标测距的结果吧:
写的有点累了,就不想过多叙述了,最后就放一下多目标测距的结果吧:
| 信号参数 |
测距范围 |
目标一 |
目标二 |
目标三 |
目标四 |
RCS |
| 第一组 |
12-16km |
12.5km |
13.5km |
14.9km |
15km |
1 |

目标压缩后的峰值时间分别为:7.613109us、14.284313us、23.615411us、24.265453us。减去补偿后除去一半再乘以光速,再加上最初的距离分别得到:12499.97m、13500.64m、14900.31m、14997.82m。最大误差2.18m,最小误差0.03m。
后面有机会再补充...文章来源:https://www.toymoban.com/news/detail-804170.html
到了这里,关于基于FPGA的脉冲压缩设计(Matlab+vivado)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!