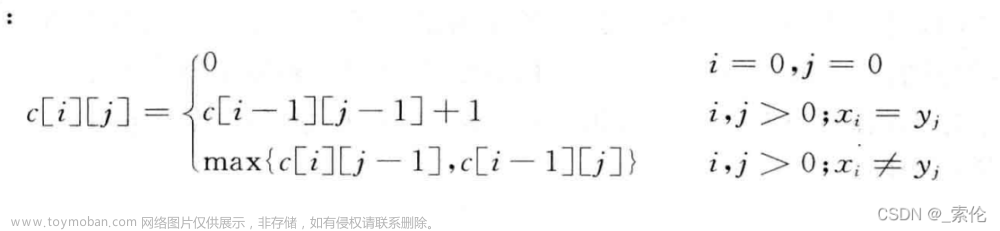leetcode1143. 最长公共子序列-动态规划(java)-Toy模板网

这篇具有很好参考价值的文章主要介绍了leetcode1143. 最长公共子序列-动态规划(java)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

leetcode1143. 最长公共子序列

leetcode1143. 最长公共子序列
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-common-subsequence

题目描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。
一个字符串的子序列是指这样一个新的字符串：
它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

示例 1：
输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。

示例 2：
输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc” ，它的长度为 3 。

示例 3：
输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：
1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。

暴力递归

解题思路

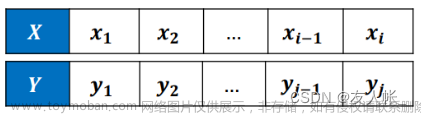
我们用指针法:
一.先把两个字符串转成两个字节数组
二.两个指针分别卡住字符数组的最右边
三.通过比较不断移动指针位置,遇到相等的就加1,不等的就不加
以上是整体思路:
具体细节.
先考虑base case .只有指针走到了头,才会停止
所以base case 就是0 位置,
知道了0位置,还要考虑哪个数组在0位置.要分开判断
然后就是普遍位置了.就是递归的过程了.
流程清楚了,代码就好写了

代码演示

    public int longestCommonSubsequence(String text1, String text2) {
        if (text1 ==null || text2 == null || text2.length() == 0 || text1.length() == 0){
            return 0;
        }
        return process(text1.toCharArray(),text2.toCharArray(),text1.length() - 1,text2.length() - 1);
    }

    /**
     *
     * @param str1 字节数组
     * @param str2 字节数组
     * @param i 字节数组str1 的下标
     * @param j 字节数组str2 的下标
     * @return
     */
    public static int process(char[]str1,char[]str2,int i,int j ){
        //base case 都在0 位置
        if(i == 0 && j == 0){
            return str1[i] == str2[j] ? 1 : 0;
        }else if (i == 0){
            //i 来到 0 位置 相等直接返回1 不等还要继续移动str2 的指针就行比较有没有相同的
            if(str1[i] == str2[j]){
                return 1;
            }else{
                return process(str1,str2,i,j - 1);
            }
        } else if (j == 0) {
            //j来到 0 位置 相等直接返回1 不等还要继续移动str1 的指针就行比较有没有相同的
            if(str1[i] == str2[j]){
                return 1;
            }else{
                return process(str1,str2,i - 1,j);
            }

        }else {
            int p1 = 0;
            int p2 = 0;
            int p3 = 0;
            if(str1[i] != str2[j]){
            	//不等时 str1 的指针和 str2 的指针 分两种情况
            	//分别进行比较
                p1 = process(str1,str2,i,j - 1);
                p2 = process(str1,str2,i - 1,j );
            }else{
            	//相等时 同时移动 子序列加1 
                p3 = 1 +   process(str1,str2,i - 1,j - 1);     
            }
            return Math.max(p1,Math.max(p2,p3));
        }
    }

动态规划

解题思路

动态规划就是对递归的改写,把递归过程,变成动态规划表生成的过程.
改写的三个步骤:
一.通过base case 先初始化能确定的值
二.通过递归过程去初始化剩余的值
三,返回递归调用的最初始状态.

代码演示

    /**
     * 动态规划
     * @param text1
     * @param text2
     * @return
     */
 public static int dp(String text1, String text2){
        char[] str1 = text1.toCharArray();
        char[] str2 = text2.toCharArray();
        int N = str1.length;
        int M = str2.length;
        int[][]dp = new int[N][M];
        //根据base case 初始化
        dp[0][0] = str1[0] == str2[0] ? 1 : 0;
        //str1 来到 0 位置时
        for (int j = 1; j < M ;j++){
            dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j - 1];
        }
        //str2 来到 0 位置时
        for (int i = 1;i < N ;i++){
            dp[i][0] = str1[i] == str2[0] ? 1 : dp[i - 1][0];
        }
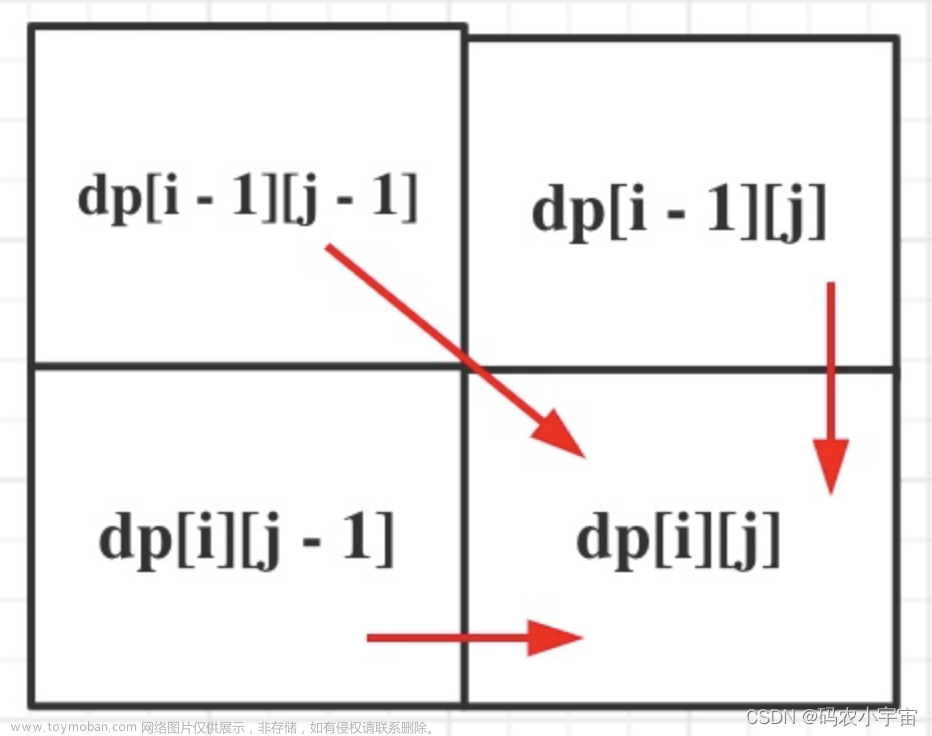
        for (int i = 1;i < N ;i++){
            for (int j = 1;j < M ;j++){
               
            int p1 = 0;
            int p2 = 0;
            int p3 = 0;
            if(str1[i] != str2[j]){
                p1 = dp[i][j - 1];
                p2 = dp[i - 1][j];
            }else{
                p3 = 1 + dp[i -1][j - 1];     
            }

                dp[i][j] =  Math.max(p1,Math.max(p2,p3));
            }
        }
        //返回递归调用的最初始状态
        return dp[N - 1][M - 1];
    }