还不会二分查找？看这一篇就够了-Toy模板网

这篇具有很好参考价值的文章主要介绍了还不会二分查找？看这一篇就够了。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、整数二分

二分查找分为整数二分和浮点数二分，一般所说的二分查找都是指整数二分。

1.1 二分查找模板

满足单调性的数组一定可以使用二分查找，但可以使用二分查找的数组不一定需要满足单调性。

不妨假设我们找到了条件 $C_1$ ，它和它的对立条件 $C_2$ 能够将数组 $a$ 一分为二，如下图所示：

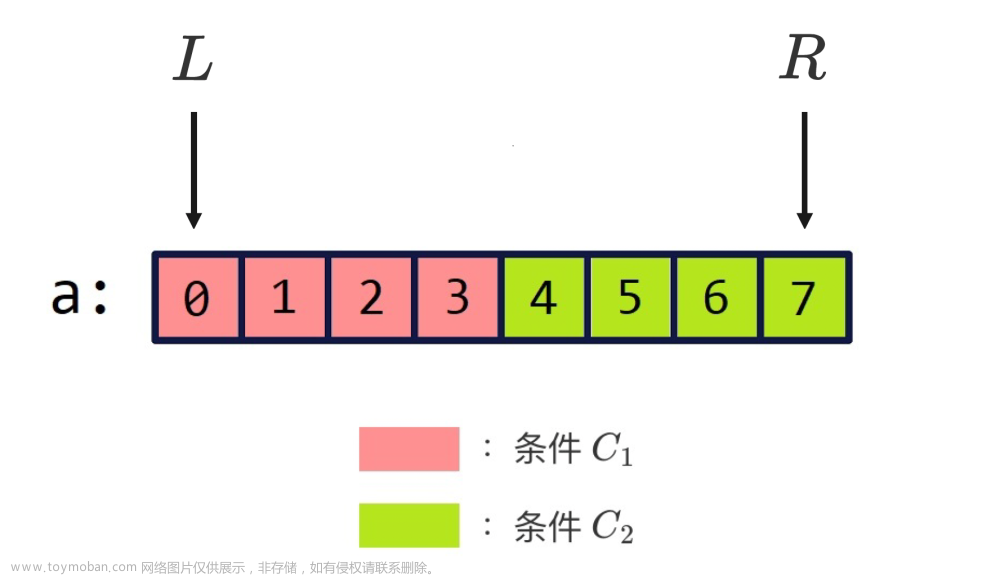
还不会二分查找？看这一篇就够了,DSA,# AcWing,c++,二分查找,算法

因为 $C_1$ 和 $C_2$ 互为对立，故总有 $C_1\cup C_2\equiv \text{True},\;C_1\cap C_2\equiv \text{False}$ （用C++语言描述，就是 c1 || !c1 总是为真，c1 && !c1 总是为假）。换句话说， $\forall \,x\in a$ ， $x$ 至少满足 $C_1$ 和 $C_2$ 中的一个，且 $x$ 不会同时满足 $C_1$ 和 $C_2$ 。

观察上图可以发现，索引 $3$ 和索引 $4$ 这两个位置都可以作为 $C_1$ 和 $C_2$ 的分界点。其中，索引 $3$ 是红色区域的右边界，索引 $4$ 是绿色区域的左边界。而我们接下来要讨论的二分查找模板就是用来寻找 $C_1$ 和 $C_2$ 的分界点的。

1.1.1 寻找右边界的二分查找

前面说过， $C_1$ 和 $C_2$ 的分界点一共有两个，因此我们的整数二分查找模板也有两个。一个用来查找右边界（即左侧的分界点，对应索引 $3$ ），一个用来查找左边界（即右侧的分界点，对应索引 $4$ ）。这里首先介绍查找右边界的模板。

因为查找的是红色区域的右边界，所以先定义一个函数 check(i)，其中参数 $i$ 是索引。当 $i$ 位于红色区域，即 $0\leq i \leq 3$ 时，check(i) 为真；当 $i$ 位于绿色区域，即 $4\leq i \leq 7$ 时，check(i) 为假。

初始时设置左右两个指针分别位于数组的左右两端，每次循环时计算 $mid=\frac{l+r}{2}$ （至于 $mi d$ 到底取多少稍后会说），然后判断 check(mid) 的值（为实现二分查找，我们需要确保每次缩小区间时答案都落在区间内。这样一来，当最终 l == r 时，l 就是我们需要的答案）。如果 check(mid) 为真，说明 $mi d$ 位于红色区域，且 $mi d$ 有可能就是右边界，因此接下来令 $l = mi d$ 来缩小查找范围（因为我们要保证缩小后的区间仍然包含答案）；如果 check(mid) 为假，说明 $mi d$ 位于绿色区域，且 $mi d$ 必不可能是红色区域的右边界，因为 $mi d$ 最多是索引 $4$ ，因此令 $r = mi d - 1$ 来缩小查找范围。

接下来重点关注 $mi d$ 到底该取多少。如果 $mid=\frac{l+r}{2}$ ，其中的除法代表整除，在某一轮循环出现了 $r - l = 1$ ，则 $mid=\frac{2l+1}{2}=l$ 。若 check(mid) 为真，则更新后的区间仍然为 $[l, r]$ ，这就会导致无限循环。事实上，只需要取 $mid=\frac{l+r+1}{2}$ ，若 check(mid) 为真，则 $mi d = r$ ，更新后的区间为 $[r, r]$ ，循环结束。若 check(mid) 为假，则更新后的区间为 $[l, l]$ ，循环结束。

寻找右边界的二分查找模板：

int right_bound(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

1.1.2 寻找左边界的二分查找

类似1.1.1节中的分析，因为查找的是绿色区域的左边界，所以先定义一个函数 check(i)，其中参数 $i$ 是索引。当 $i$ 位于绿色区域，即 $4\leq i \leq 7$ 时，check(i) 为真；当 $i$ 位于红色区域，即 $0\leq i \leq 3$ 时，check(i) 为假。

初始时设置左右两个指针分别位于数组的左右两端，每次循环时计算 $mid=\frac{l+r}{2}$ （至于 $mi d$ 到底取多少稍后会说），然后判断 check(mid) 的值。如果 check(mid) 为真，说明 $mi d$ 位于绿色区域，且 $mi d$ 有可能就是左边界，因此接下来令 $r = mi d$ 来缩小查找范围；如果 check(mid) 为假，说明 $mi d$ 位于红色区域，且 $mi d$ 必不可能是绿色区域的左边界，因为 $mi d$ 最多是索引 $3$ ，因此令 $l = mi d + 1$ 来缩小查找范围。

接下来重点关注 $mi d$ 到底该取多少。如果 $mid=\frac{l+r}{2}$ ，其中的除法代表整除，在某一轮循环出现了 $r - l = 1$ ，则 $mid=\frac{2l+1}{2}=l$ 。若 check(mid) 为真，则更新后的区间为 $[l, l]$ ，循环结束。若 check(mid) 为假，则更新后的区间为 $[r, r]$ ，循环结束。综上所述， $mi d$ 取 $\frac{l+r}{2}$ 即可。

寻找左边界的二分查找模板：

int left_bound(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

1.2 应用：寻找元素的起始位置和终止位置

原题链接：AcWing 789. 数的范围

以 a = [1, 3, 3, 3, 4] 为例，数字 $3$ 的起始位置和终止位置分别是 $1$ 和 $3$ （索引）。如何利用1.1节中的模板来完成此题呢？

现对数组 $a$ 作出划分，若令 $C_1:a[i]<x,\; C_2:a[i]\geq x$ （注意必须保证 $C_1,C_2$ 互为对立），则求 $x$ 的起始位置便转化成了求 $C_2$ 区域的左边界。若令 $C_1:a[i]\leq x,\; C_2:a[i]> x$ ，则求 $x$ 的终止位置便转化成了求 $C_1$ 区域的右边界。

在求 $C_2$ 区域的左边界时，check(mid) 即为 a[mid] >= x。在求 $C_1$ 区域的右边界时，check(mid) 即为 a[mid] <= x。

AC代码如下：

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int a[N];

int left_bound(int l, int r, int x) {
    while (l < r) {
        int mid = l + r >> 1;
        if (a[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return l;
}

int right_bound(int l, int r, int x) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (a[mid] <= x) l = mid;
        else r = mid - 1;
    }
    return l;
}

int main() {
    int n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i++) cin >> a[i];

    while (q--) {
        int k;
        cin >> k;
        int begin = left_bound(0, n - 1, k);
        if (a[begin] != k) cout << "-1 -1" << endl;
        else cout << begin << " " << right_bound(0, n - 1, k) << endl;
    }

    return 0;
}

二、浮点数二分

2.1 浮点数二分模板

相比整数二分，浮点数二分就要简单许多了，因为浮点数二分不涉及到边界问题。

浮点数二分通常用来求某个数 $x$ 的近似值（ $x$ 不易直接求得，例如 $x=\sqrt{2}$ 等）。由于此时左右两个指针也均为浮点数，所以我们不能直接判断 l == r，而是判断 r - l 是否小于预先设定的精度。

模板如下：

double fbsearch(double l, double r, double eps) {
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

一些注意事项：

若要求精确到小数点后 $k$ 位，则 $e p s$ 取 $10^{-(k+2)}$ ;
若 $mid\geq x$ ，则 check(mid) 为真，否则为假。

2.2 应用：数的三次方根

原题链接：AcWing 790. 数的三次方根

注意到当 $∣ x ∣ < 1$ 时，有 $x^{1/3}|>|x|$ ，故选取 $l, r$ 时一定要谨慎。

因为 $10000^{1/3}<22$ ，所以这里取 $l=-22,\,r=22$ 即可。

#include <iostream>

using namespace std;

double x;

double fbsearch(double l, double r, double eps) {
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (mid * mid * mid >= x) r = mid;
        else l = mid;
    }
    return l;
}

int main() {
    cin >> x;
    printf("%lf", fbsearch(-22, 22, 1e-8));
    return 0;
}

三、使用STL进行二分查找

3.1 std::binary_search

template< class ForwardIt, class T >
bool binary_search( ForwardIt first, ForwardIt last, const T& value );

该函数用来检查 [first, last) 区间内（该区间已排序）是否有数字等于 value，如果有返回 true，否则返回 false。

3.2 std::lower_bound

template< class ForwardIt, class T >
ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value );

该函数用来返回 [first, last) 区间内（该区间已排序）首个大于等于 value 的元素的迭代器，如果找不到这种元素则返回 last。

3.3 std::upper_bound

template< class ForwardIt, class T >
ForwardIt upper_bound( ForwardIt first, ForwardIt last, const T& value );

该函数用来返回 [first, last) 区间内（该区间已排序）首个大于 value 的元素的迭代器，如果找不到这种元素则返回 last。

3.4 std::equal_range

template< class ForwardIt, class T >
std::pair<ForwardIt, ForwardIt>
    equal_range( ForwardIt first, ForwardIt last, const T& value );

该函数用来返回 [first, last) 区间内（该区间已排序）所有等于 value 的元素的「范围」。

「范围」实际上是由两个迭代器构成的 pair。pair 中的第一个元素是 std::lower_bound 的返回值，pair 中的第二个元素是 std::upper_bound 的返回值。

接下来我们用STL来简化1.2节中的代码。

注意到对于数组而言，其迭代器就是指针，因此我们可以通过将返回的迭代器与数组名作差来得到迭代器所指向的元素的下标。

简化后的代码如下：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int a[N];

int main() {
    int n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i++) cin >> a[i];

    while (q--) {
        int k;
        cin >> k;
        auto p = equal_range(a, a + n, k);
        if (*p.first != k) cout << "-1 -1" << endl;
        else cout << p.first - a << " " << p.second - a - 1 << endl;
    }

    return 0;
}

References

[1] https://www.acwing.com/activity/content/punch_the_clock/11/
[2] https://www.acwing.com/blog/content/31/
[3] https://zh.cppreference.com/w/cpp/algorithm/lower_bound文章来源地址https://www.toymoban.com/news/detail-804568.html

到了这里，关于还不会二分查找？看这一篇就够了的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！