本章内容
本章主要介绍矩阵分解常用的三种方法,分别为:
1
◯
\textcircled{1}
1◯特征值分解
2
◯
\textcircled{2}
2◯奇异值分解
3
◯
\textcircled{3}
3◯Funk-SVD
矩阵分解原理:
\textbf{\large 矩阵分解原理:}
矩阵分解原理: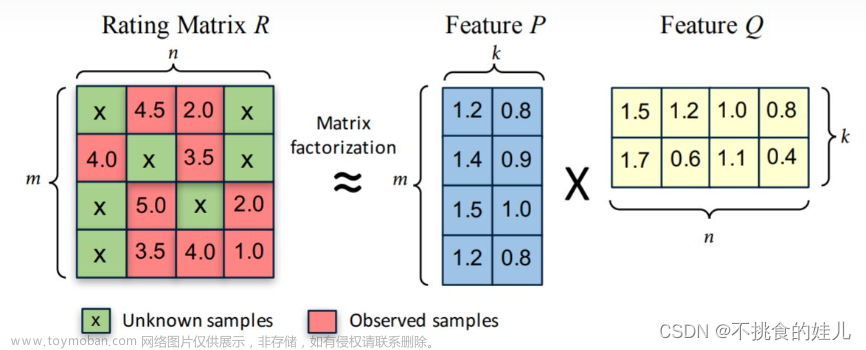
矩阵分解算法将
m
×
n
m\times n
m×n 维的矩阵
R
R
R分解为
m
×
k
m \times k
m×k的用户矩阵
P
P
P和
k
×
n
k \times n
k×n维的物品矩阵
Q
Q
Q相乘的形式。其中
m
m
m为用户的数量,
n
n
n为物品的数量,
k
k
k为隐向量(Latent Factor)的维度。
k
k
k的大小决定了隐向量表达能力的强弱,实际应用中,其取值要经过多次的实验来确定。在得到了
P
P
P用户矩阵和物品矩阵
Q
Q
Q后,将两个矩阵相乘,就可以得到一个满秩的矩阵。那么,我们就对未被评价过的物品,有了一个预测评分。接下来,可以将评分进行排序,推荐给用户。这就是矩阵分解对于推荐系统最基本的用途。
矩阵分解的目的就是通过分解之后的两矩阵内积,来填补缺失的数据,用来做预测评分。矩阵分解的核心是将矩阵分解为两个低秩的矩阵的乘积,分别以
k
k
k维的隐因子向量表示,用户向量和物品向量的内积则是用户对物品的偏好度,即预测评分。值得注意的是
k
k
k的选取是通过实验和经验而来的,因此矩阵分解的可解释性不强。
一、特征值分解
\textbf{\large 一、特征值分解}
一、特征值分解
A
A
A为
n
n
n阶矩阵,若数
λ
\lambda
λ和
n
n
n维非0列向量
v
⃗
\vec{v}
v满足
A
v
⃗
A \vec{v}
Av =
λ
\lambda
λ
v
⃗
\vec{v}
v,那么数
λ
\lambda
λ称为
A
A
A的特征值,
v
⃗
\vec{v}
v称为
A
A
A的对应于特征值
λ
\lambda
λ的特征向量。
可以这样理解: λ \lambda λ为矩阵变换的大小, v ⃗ \vec{v} v为矩阵变换的方向。但是特征值只能用于方阵,对推荐系统用户——物品的矩阵还不太适合。
特征值分解,就是将矩阵
A
A
A分解为如下式:
A
=
Q
Σ
Q
−
1
A = Q \Sigma Q^{-1}
A=QΣQ−1
Q Q Q是矩阵 A A A的特征向量组成的矩阵,Σ则是一个对角阵,对角线上的元素就是特征值。我们来分析一下特征值分解的式子,分解得到的Σ矩阵是一个对角矩阵,里面的特征值是由大到小排列的,这些特征值所对应的特征向量就是描述这个矩阵变换方向(从主要的变化到次要的变化排列)。
我们通过特征值分解得到的前N个特征向量,就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵变换。也就是说:提取这个矩阵最重要的特征。

二、奇异值分解
\textbf{\large 二、奇异值分解}
二、奇异值分解
假设一个矩阵
M
M
M是一个
m
×
n
m \times n
m×n的矩阵,则一定存在一个分解:
M
=
U
Σ
V
T
M = U\Sigma V^T
M=UΣVT
其中 U U U是 m × m m\times m m×m的正交矩阵, V V V是 n × n n\times n n×n的正交矩阵, Σ \Sigma Σ是 m × n m\times n m×n的对角矩阵。 Σ \Sigma Σ对角线上的元素就称为 M M M的奇异值。
例如:
假设矩阵
A
A
A如下:
矩阵
A
A
A为
6
×
4
6\times 4
6×4的用户评分矩阵,6个用户对4个物品一共有19个评分,0代表没评分。
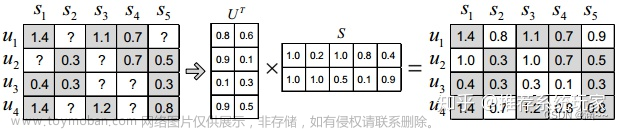
使用SVD进行分解得到:


分解后,
U
U
U矩阵为
6
×
6
6\times6
6×6的正交矩阵,
V
V
V为
4
×
4
4\times4
4×4的正交矩阵。
S
S
S为对角矩阵即公式中的
Σ
\Sigma
Σ。选取
S
S
S中较大的
k
k
k个元素作为隐含特征。删除
S
S
S的其他维度以及
U
U
U和
V
V
V对应的维度,矩阵分解就完成了。
我们可以使用最大的 k k k个值和对应大小的 U U U、 V V V 矩阵来近似描述原始的评分矩阵。这就是SVD做降维用法的核心思想。
我们在这里选择
k
k
k=2,那么
S
S
S对角矩阵就降维成:
同样,
U
U
U矩阵变成了
6
×
2
6\times2
6×2维,
V
V
V矩阵变成了
4
×
2
4\times2
4×2维,然后将处理过的USV三个矩阵相乘做内积,可以得到新的矩阵
A
2
A2
A2为:
此时,
A
2
A2
A2和A数据很接近,同时又补充了空白部分。
三、Basic
Matrix
Factorization(Funk-SVD)
\textbf{\large 三、Basic Matrix Factorization(Funk-SVD)}
三、Basic Matrix Factorization(Funk-SVD)
Funk-SVD的基本思想就是:既然评价指标是均方根误差(Root Mean Squared Error, RMSE),那么可以直接通过训练集中的观察值利用最小化RMSE学习用户特征矩阵P和物品特征矩阵Q。为方便表示,用U表示用户的集合,D表示物品的集合,R表示用户评分矩阵。通过这种方法用户和物品可以被映射到一个K维(K可以自己设置)的潜在特征空间。通过挖 掘用户的潜在特征矩阵P(|U|xK维)和物品潜在特征矩阵Q(|D|xK维)来估计评分。即通过下式来得到评分矩阵:
R
≈
P
×
Q
T
=
R
^
R \approx P \times Q^T = \hat{R}
R≈P×QT=R^
因此利用上述公式,可以计算出用户i对物品j的估计评分
r
i
j
^
\hat{r_{ij}}
rij^为:
r
i
j
^
=
p
i
q
j
T
=
∑
k
=
1
K
p
i
k
q
k
j
\hat{r_{ij}} = p_iq_j^T = \sum_{k=1}^K p_{ik} q_{kj}
rij^=piqjT=k=1∑Kpikqkj
其中 p i ∈ R K p_i\in R^K pi∈RK表示用户i的K维潜在特征,表达用户的内部特性; q j ∈ R K q_j\in R^K qj∈RK表示物品j的K维潜在特征,表达物品的内部特性。
对于每个用户评分
r
i
j
r_{ij}
rij,使用FunkSVD进行矩阵分解,对应的估计评分为
p
i
T
q
j
p_i^Tq_j
piTqj,采用均方差做损失函数为
e
i
j
=
(
r
i
j
−
p
i
q
j
T
)
2
e_{ij} =(r_{ij} -p_iq_j^T)^2
eij=(rij−piqjT)2,我们的期望就是使均方差误差尽可能的小,考虑到所有的用户和物品组合,我们的优化目标函数J(p,q)为:
m
i
n
p
∗
,
q
∗
∑
i
,
j
∈
M
(
r
i
j
−
p
i
q
j
T
)
2
\mathop{min}_{p^*,q^*} \sum_{i,j\in M} (r_{ij} -p_i q_j^T)^2
minp∗,q∗i,j∈M∑(rij−piqjT)2
为防止过拟合(过拟合是指模型在训练集上误差很小,但是在测试集上表现很差(即泛化能力 [generalization ability] 差),),加入正则化项(类似惩罚函数,利用先验知识进行约束),损失函数即为:
L o s s = a r g m i n ∑ i , j ( r i j − p i q j T ) 2 + ( ∣ ∣ p i ∣ ∣ + ∣ ∣ q j ∣ ∣ ) 2 Loss = argmin \sum_{i,j}(r_{ij} -p_i q_j^T)^2 + (||p_i||+||q_j||)^2 Loss=argmini,j∑(rij−piqjT)2+(∣∣pi∣∣+∣∣qj∣∣)2文章来源:https://www.toymoban.com/news/detail-804741.html
然后使用梯度下降算法来拟合原矩阵。文章来源地址https://www.toymoban.com/news/detail-804741.html
到了这里,关于矩阵分解(Matrix-Factorization)无门槛的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!