写在前面
分治
动态规划本篇 还差一堆
贪心
网络流
首先,怕误人子弟必须声明一下本人很菜(越复习越觉得完蛋了 作为一个科班研究生算法学成这样非常惭愧(跪 ,可能写的都不是很懂,很多内容打算背过去了。因为我发现好像真的有人看所以多提醒一句。。(大家就只食用目录吧
其次,本文只也许够应付考试,个人使用。而且其实就是ppt内容只是我自己喜欢这样整理。虽然全力理解内容且认真书写但也可能存在错误,如有发现麻烦指正,谢谢🌹
最后,因为不知道考试怎么考,本人的复习方式是照着目录讲一遍自己的理解+写伪代码(如果来的及会再做一个综合纯享版),再做一下上课讲过的例题和作业(印象里只有主定理、FFT、网络流上课练习+分治和动规两次作业)。
文章持续更新中,或许考前能发完也可能发不完。
祝我们好运🌹
动态规划
动机: 在递归求解的过程中重复求解子问题
策略: 空间换时间——将子问题保存下来避免重复计算
- 空间:子问题的数量(由子问题的参数决定)
关键:找到正确且高效的递归关系
求解:自顶向下/自底向上备忘录递归,自底向上没有递归调用的时空开销。
当难以建立递归关系考虑以下两种方案:
- 增加约束条件
- 增加参数
思路:
- 建立一个新的表示
- 基于这个新表示转化原问题
- 考虑基本情况
- 考虑归纳步骤
最重要的还是写归纳步骤的递归关系,想不出来那万事休矣。
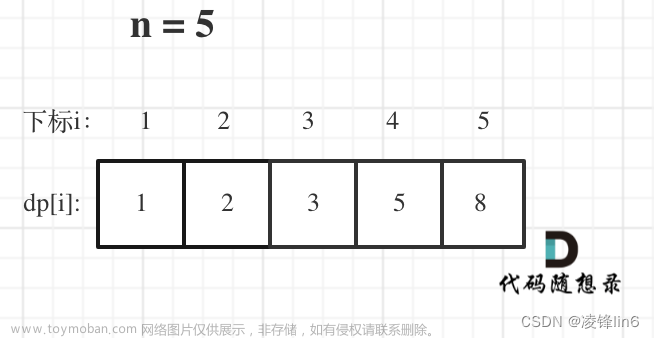
斐波那契
1.递归
直接递归求解存在很多重复计算故考虑将历史记录保存
2.自顶向下动规(被动备忘录)

3.自底向上动规(主动备忘录)
从小到大计算
4.进一步优化(空间优化)
上一步的自底向上递归保存了所有的f(n),但实际上对于斐波那契当前需要求解的n的值来说只有n-1和n-2是有用的故只保存当前的数和前两个数,用三个变量即可。
二项式系数
1.递归
二项式系数是可以用C(N,K)直接求解的,但是大数计算容易溢出。
考虑数学的方式拆分组合数做递归
仍然是存在重复运算
2.自顶向下动规(被动备忘录)
都是一个套路的
3.自底向上动规(主动备忘录)
也是从小到大直接算,这里可以考虑不同的填写顺序
4.进一步优化(空间优化)
仍然是不需要过多的变量存储
树的最大独立集
1.问题定义

所谓树的独立集:两两不相邻顶点构成的集合。
而最大独立集:不被其他独立集包含即为最大。
问题就是给定一棵树返回最大独立集。
2.递归关系①
如何考虑这个问题:顶点在不在独立集里。
所以问题的解只有两种情况:
自底向上递归直接用树存储伪码:
这里面孩子用的递归调用孙子直接x.MIS暂且理解成x.MIS可以直接从备忘录读取
下面的也是一样的
3.递归关系②
仍然是考虑父节点在不在独立集里,只是换一种定义:
最长递增子序列-(作业)
子序列:序列顺序不变,可以不连续。
求解s[1 … n]的最长子序列
1.难以建立递归关系的两个解决方案
考虑递归求解一般的思路:知道了n-1的情况求n
假设知道了前n-1的最长递增子序列的长度,但是不知道n能不能放进去。
如果同时知道了n-1的长度和最后一个是几呢?知道n能不能放进去了。但是如果n不能放进去,也有可能存在另一个n-1序列能把n放进去。
但是又不可能把所有的序列记录。
当难以建立递归关系考虑以下两种方案
- 增加约束条件:比如定义L(k)是以 k结尾/以k开头 的最长子序列的长度
- 增加参数:定义L(i,j)中的 s(j…n)所有数都大于s[i]/小于s[i] 的最长子序列长度 *注意i和j是什么
2.增加约束自底向上动规
定义L(k)是以 k结尾 的最长子序列的长度
重新定义原问题:求解max L(k) (1<=k<=n)
考虑基本情况:k=1: L(k)=1
考虑递归关系:L(k) = max{1, max{L(i)+1}(i∈(1,k-1),如果s[k]>s[i]可以加上s[k],选最大的)} 记得跟1比。
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
一个例子:
反过来定义是一样的
关于作业问过的返回序列:
(简单贴一下我写的
思路:使用一个额外的数组来记录以每个位置结尾的最长递增子序列。当找到全局的最长递增子序列长度时,可以根据这个信息来重建最长递增子序列。具体见代码实现。
int lis_dp1(const vector<int>& s, int n) {
// insert code here...
// let the L(k) means the LIS's last number is s[k]. the question is to get max(L(k))
vector<int> L1(n);
int answer = 1;
for(int k=0;k<=n;k++){
if(k==0){
L1[k]=1;
}
else{
for(int i=0;i<=k-1;i++){
if(s[k]>s[i]){
L1[k] = max(L1[k],L1[i]+1);
}
L1[k] = max(1,L1[k]);
}
}
answer = max(answer,L1[k]);
// cout<<L1[k]<<endl;
}
return answer;
}
vector<int> find_lis_dp1(const vector<int>& s, int n) {
// insert code here...
n++;
vector<int> L1(n, 1);
vector<int> prev_index(n, -1);
int max_length = 1;
int end_index = 0;
for (int k = 1; k < n; k++) {
for (int i = 0; i < k; i++) {
if (s[k] > s[i] && L1[k] < L1[i] + 1) {
L1[k] = L1[i] + 1;
prev_index[k] = i;
}
}
if (L1[k] > max_length) {
max_length = L1[k];
end_index = k;
}
}
vector<int> result;
while (end_index != -1) {
result.insert(result.begin(), s[end_index]);
end_index = prev_index[end_index];
}
return result;
}
3.增加子问题参数自底向上动规
定义L(i,j)中的 s(j…n)所有数都大于s[i] 的最长子序列长度
原问题转化:求L(0,1),s[0] = -∞
基本情况:j>n L(i,j)=0(二维数组边界)
递归关系:
时间空间复杂度都是
O
(
n
2
)
O(n^2)
O(n2)
定义成都小于s[i]也是一样的。
int lis_dp2(const vector<int>& s, int n) {
// insert code here...
n++; //number
vector<int> ss(n+1); //0-9 10
for(int i=0;i<=n;i++){
if(i==0) ss[i]=INT_MIN;
else ss[i]=s[i-1];
}
int matrics_length = n+2;
vector<vector<int>> L2(matrics_length,vector<int>(matrics_length));
for(int j=matrics_length-2;j>=0;j--){
for(int i=matrics_length-2;i>=0;i--){
if(j>n) L2[i][j]=0;
else if(ss[i]>=ss[j]){
L2[i][j]=L2[i][j+1];
}
else{
L2[i][j]=max(L2[i][j+1],1+L2[j][j+1]);
}
}
}
return L2[0][1];
}
vector<int> find_lis_dp2(const vector<int>& s, int n) {
// insert code here...
n++;
vector<int> ss(n + 1);
for (int i = 0; i <= n; i++) {
if (i == 0) ss[i] = INT_MIN;
else ss[i] = s[i - 1];
}
int matrics_length = n + 2;
vector<vector<int>> L2(matrics_length, vector<int>(matrics_length));
for (int j = matrics_length - 2; j >= 0; j--) {
for (int i = matrics_length - 2; i >= 0; i--) {
if (j > n) L2[i][j] = 0;
else if (ss[i] >= ss[j]) {
L2[i][j] = L2[i][j + 1];
}
else {
L2[i][j] = max(L2[i][j + 1], 1 + L2[j][j + 1]);
}
}
}
int length = L2[0][1];
vector<int> result;
int i = 0, j = 1;
while (j < matrics_length - 1) {
if (ss[i] < ss[j] && L2[i][j] == 1 + L2[j][j + 1]) {
result.push_back(ss[j]);
i = j;
}
j++;
}
return result;
}
- 贴一下反过来的:

4.对第一种思路进一步加约束优化
- key:对于长度为k的最长递增子序列,只需要记住末尾元素最小的。
-

时间复杂度:O(logn)
int lis_dp3(const vector<int>& s, int n) {
// insert code here...
vector<int> last(1);
last[0]=INT_MIN;
for(int k=0;k<=n;k++){
if(k==0){
last.insert(last.end(),s[k]);
}
else{
int last_id = last.size()-1;
if(s[k]>last[last_id]){
last.insert(last.end(),s[k]);
}
else{
for(int i=last_id;i>=0;i--){
if(s[k]>last[i]){
last[i+1]=s[k];
break;
}
}
}
}
// cout<<"k="<<k<<" s[k]="<<s[k]<<" last:"<<last<<endl;
}
return last.size()-1;
}

编辑距离
1.问题定义
需要编辑的个数和为编辑距离,目标是让一个字符串转成另外一个让编辑距离最小。
提出序列比对:可视化修改字符串的过程。上行为原字符串,下行为需要更改的。第一行的空格表示插入第二行空格表示删除。上下不同的个数和就是编辑距离。
3. 递归关系
思路:考虑最后一列。
我觉得其实这个二位数组可以这样理解:填写顺序从左上到右下,每填写一个格子,这个格子所在的行和列就全都填写完。向右和向下是插入或者删除,而向右下就是在替换。
2. 例子

上面图对应的三条路
Hischberg’s algorithm
上面的改进:用O(m+n)空间构造最优比对
直觉上是创建一个编辑图,求左上到右下的最短路径
我觉得不会考QAQ
最长公共子序列
最优二叉搜索树
交替拿硬币
石子合并
背包
每个物品存在价值v和重量w,给定背包最大承重W求如何放让价值最大。
递归关系
思路:考虑已知前n-1个物品的最优解,最后一个能不能放,能放的话放或不放取最优。
基本情况:n=0 那价值为零
乘坐电梯
1.问题描述
n个人,给出体重w[n]
电梯承重x
问最少几趟电梯能把人送下去
2.思路
考虑知道了n-1个人的最优解,最后一个人考虑能不能装进任何一趟,不能就新开一个。
问题在于这个最后一个人的选择,这是一个运送顺序的问题。
把假设扩大:文章来源:https://www.toymoban.com/news/detail-805007.html
- 假设对{1 … n}的任意子集c,可以计算他的最优运送B( c )
- 这个B( c )需要记录两个值:B( c ).first运送趟数,
吃个饭先文章来源地址https://www.toymoban.com/news/detail-805007.html
3.例子
到了这里,关于【算法设计与分析】(三)动态规划_更新中:斐波那契、二项式系数、树的最大独立集、最长递增、公共子序列、编辑距离、Hischberg、最优二叉搜索树、交替拿硬币、石子合并、背包、乘电梯的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!