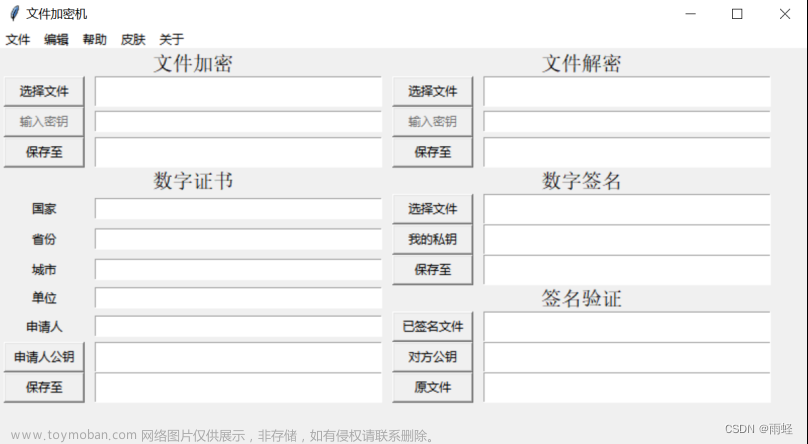
目录
一.加解密算法
数字签名
对称加密
DES(Data EncryptionStandard)
3DES(Triple DES)
AES(Advanced EncryptionStandard)
RSA加密法
DSA(Digital SignatureAlgorithm)
ECC(Elliptic CurvesCryptography)
非对称加密
签名与加密过程
非对称加密的应用
对称加密与非对称加密的结合
二.数字证书
图解
一.加解密算法
加密简单而言就是通过一种算法将明文信息转换成密文信息,信息的的接收方能够通过密钥对密文信息进行解密获得明文信息的过程。根据加解密的密钥是否相同,算法可以分为对称加密、非对称加密、对称加密和非对称加密的结合。
数字签名
数字签名的基本原理就是用私钥去签名,而用公钥去验证签名

对称加密
对称加密顾名思义就是加密和解密的密钥是相同的

DES(Data EncryptionStandard)
数据加密标准,速度较快,适用于加密大量数据的场合.经典的分组加密算法,1977年由美国联邦信息处理标准(FIPS)采用FIPS-46-3,将64位明文加密为64位的密文,其密钥长度为64位(包含8位校验位)。现在已经很容易被暴力破解
3DES(Triple DES)
基于DES,对一块数据用三个不同的密钥进行三次加密,强度更高.但现在也被认为不够安全;
AES(Advanced EncryptionStandard)
AES也为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。 在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的分组长度可以使用128位、 192位或256位。密钥的长度不同,推荐加密轮数也不同。AES的优势在于处理速度快,整个过程可以用数学描述,目前尚未有有效的破解手段;
RSA加密法
RSA 公司发明,是一个支持变长密钥的公共密钥算法,需要加密的文件块的长度也是可变的
DSA(Digital SignatureAlgorithm)
数字签名算法,是一种标准的DSS(数字签名标准),严格来说不算加密算法
ECC(Elliptic CurvesCryptography)
椭圆曲线密码编码学.ECC和RSA相比具有多方面的绝对优势,主要有:抗攻击性强.相同的密钥长度,其抗攻击性要强很多倍.计算量小,处理速度快.ECC总的速度比RSA、DSA要快得多.存储空间占用小.ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多,意味着它所占的存贮空间要小得多.这对于加密算法在IC卡上的应用具有特别重要的意义.带宽要求低.当对长消息进行加解密时,三类密码系统有相同的带宽要求,但应用于短消息时ECC带宽要求却低得多.带宽要求低使ECC在无线网络领域具有广泛的应用前景
现代备受关注的算法系列,基于对椭圆曲线上特定点进行特殊乘法逆运算难以计算的特性。最早在1985年由Neal Koblitz和Victor Miller分别独立提出。ECC系列算法一般被认为具备较高的安全性,但加解密计算过程往往比较费时;
非对称加密
非对称加密算法中,加密密钥和解密密钥是不同的,分别称为公钥(public key)和私钥(private key)。私钥一般需要通过随机数算法生成,公钥可以根据私钥生成。公钥一般是公开的,他人可获取的;私钥一般是个人持有,他人不能获取。
目前普遍认为RSA类算法可能在不远的将来被破解,一般推荐可采用安全强度更高的椭圆曲线系列算法,ECC将会是今后最重要的主流公钥加密技术。
签名与加密过程
签名是用私钥来完成的,用公钥来验签。加密是用公钥来加密,私钥来解密的。为什么会需要签名呢?
需要两个密钥来进行加密和解密,公开密钥(public key,简称公钥)和私有密钥(private key,简称私钥) ,公钥加密的信息只有私钥才能解开,私钥加密的信息只有公钥才能解开。这个公钥和私钥必须是一对的,如果用公钥对数据进行加密,那么只有使用对应的私钥才能解密,所以只要私钥不泄露,那么我们的数据就是安全的。
我们先假设A给B发送信息,A拥有自己的私钥(PRI_A)和公钥(PUB_A),B拥有自己的私钥(PRI_B)和公钥(PUB_B)。 B接收到消息,要怎样才能知道消息是谁发出的。或者换句话说,A发出一则消息,要怎样让接收方知道是A发出的。这时就需要A用PRI_A对信息进行签名,相当于生成了唯一的身份证。
可以这样描述以上图示过程,A向B发送信息的整个签名和加密的过程:
- A先用自己的私钥(PRI_A)对信息(一般是信息的摘要)进行签名;
- A接着使用B的公钥(PUB_B)对信息内容和签名信息进行加密。
这样当B接收到A的信息后,获取信息内容的过程:
- 用自己的私钥(PRI_B)解密A用B的公钥(PUB_B)加密的内容;
- 得到解密后的明文后用A的公钥(PUB_A)解签A用A自己的私钥(PRI_A)的签名。
注意,公钥是公开出去的,但是私钥只能是自己拥有。以上图示过程和签名加密机制保证了端到端的唯一确认。A的签名只有A的公钥才能解签,这样B就能确定是A发出的信息;A的加密只有B的私钥才能解密,因为是用B的公钥加密的,这样保证了信息只能被B读取。
非对称加密的应用
应用最广泛的是银行,银行把每个人的私钥存储在每个人的U盾里,这就相当于,只有解密方自己拥有自己的私钥,银行用你设置的公钥对你的账户进行加密,要解密必须用到自己U盾里的私钥。这就是非对称加密的广泛使用原理。
对称加密与非对称加密的结合
这种结合方式分为两个阶段,阶段一利用非对称加密对密钥进行加密传递给接收方,阶段二利用对称加密对明文信息进行加解密。如下图所示:

二.数字证书
图解
(1)鲍勃有两把钥匙:一把是公钥,一把是私钥

(2)鲍勃把公钥送给了他的朋友:帕蒂,道格,苏珊

(3)苏珊要给鲍勃写一封保密的信。她写完后用鲍勃的公钥加密,就可以达到保密效果

(4)鲍勃收到信后,用私钥解密,就看到信件的内容。这里要强调的是,只要鲍勃的私钥不泄露,这封信就是安全的,即使落在别人手里,也无法解密

(5)鲍勃给苏珊回信,决定采用“数字签名”。他写完后,先用Hash函数,生成信件的摘要(digest)

(6)鲍勃将这个签名,附在信件下面,一起发给苏珊

(7)苏珊收到信后,取下数字签名,用鲍勃的公钥解密,得到信件的摘要。由此证明,这封信确实是鲍勃发出的

(8)苏珊再对信件本身使用Hash函数,将得到的结果,与上一步得到的摘要进行对比。如果两者一致,就证明这封信没被修改过

(9)复杂的情况出现了:道格想要欺骗苏珊,他偷偷地使用了苏珊的电脑,用自己的公钥换走了鲍勃的公钥。此时,苏珊实际上拥有的是道格的公钥,但是她还认为这是鲍勃的公钥。因此,道格可以冒充鲍勃,用自己的私钥做成“数字签名”,发信给苏珊,让苏珊用假的鲍勃公钥进行解密

(10)后来,苏珊感觉不对劲,发现自己无法确定公钥是否真的属于鲍勃。她想到了一个办法,要求鲍勃去找“证书中心CA”,为公钥做认证。证书中心用自己的私钥,对鲍勃的公钥和一些相关信息一起加密,生成“数字证书”

(11)鲍勃拿到数字证书后,就可以放心了。以后再给苏珊写信,只要在签名的同时,附上数字证书就可以了

(12)苏珊收到信后,用CA的公钥解开数字证书,就可以拿到鲍勃真实的公钥了,然后就可以证明“数字签名”是否真的属于鲍勃文章来源:https://www.toymoban.com/news/detail-805072.html
详细了解数字证书,查看维基百科:https://zh.wikipedia.org/wiki/%E5%85%AC%E9%96%8B%E9%87%91%E9%91%B0%E8%AA%8D%E8%AD%89文章来源地址https://www.toymoban.com/news/detail-805072.html
到了这里,关于区块链之加解密算法&数字证书的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!