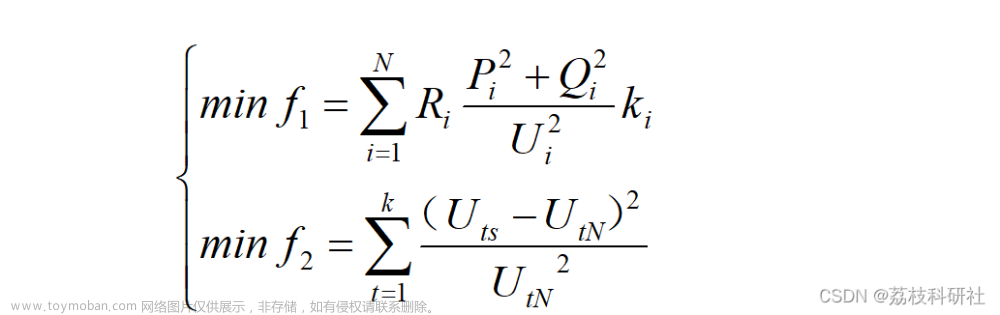多目标优化算法：基于非支配排序的鱼鹰优化算法（NSOOA）MATLAB-Toy模板网

这篇具有很好参考价值的文章主要介绍了多目标优化算法：基于非支配排序的鱼鹰优化算法（NSOOA）MATLAB。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、鱼鹰优化算法

鱼鹰优化算法（Osprey optimization algorithm，OOA）由Mohammad Dehghani 和 Pavel Trojovský于2023年提出，其模拟鱼鹰的捕食行为。具有寻优能力强、收敛速度快等特点。

鱼鹰优化算法的流程如下：
1. 初始化：设定算法参数，包括鱼鹰数量、迭代次数、搜索空间等。
2. 阶段一：定位和捕鱼（探索阶段）。
- 每只鱼鹰根据当前位置和速度进行位置更新。
- 计算每只鱼鹰的适应度值，即目标函数值。
- 根据适应度值对鱼鹰进行排序，选择适应度较好的鱼鹰作为水下鱼类。
- 每只鱼鹰根据水下鱼类的位置调整自己的速度和位置。
3. 阶段二：把鱼带到合适的位置（开发阶段）。
- 每只鱼鹰根据当前位置和速度进行位置更新。
- 计算每只鱼鹰的适应度值。
- 根据适应度值对鱼鹰进行排序，选择适应度较好的鱼鹰作为水下鱼类。
- 每只鱼鹰根据水下鱼类的位置调整自己的速度和位置。
4. 重复进行阶段一和阶段二，直到达到设定的迭代次数。
5. 输出最佳鱼鹰的位置作为优化结果。

Python：鱼鹰优化算法（Osprey optimization algorithm，OOA）求解23组基本测试函数-CSDN博客

二、基于非支配排序的鱼鹰优化算法

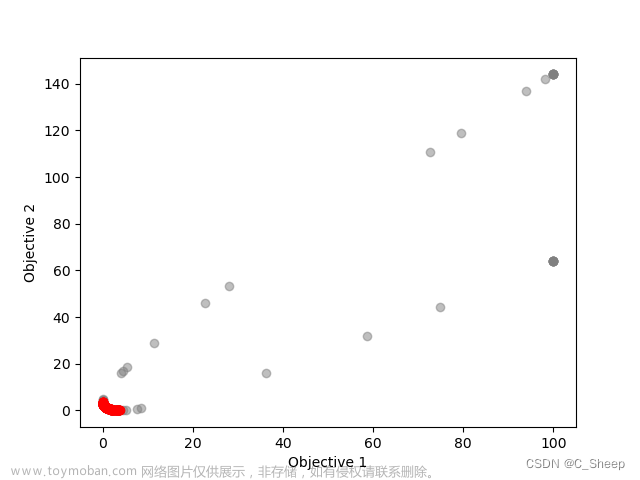
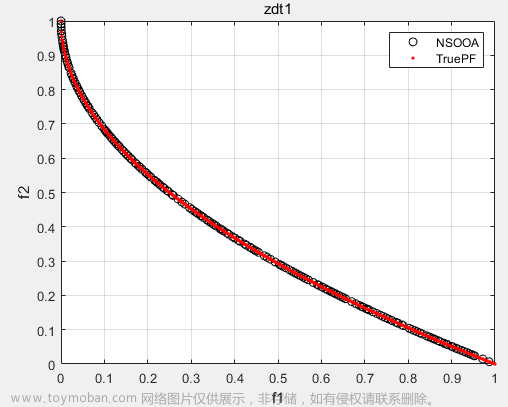
非支配排序的鱼鹰优化算法（Non-Dominated Sorting Osprey optimization algorithm，NSOOA）由OOA融合非支配排序策略而成，为了验证所提的NSOOA的有效性，将其在46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）上实验，并采IGD，GD，HV，SP四种评价指标进行评价。

（1）部分代码

close all;
clear ; 
clc;
%%
% TestProblem测试问题说明：
%一共46个多目标测试函数，详情如下：
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12：DZDT1-DZDT7
%13-22：wfg1-wfg10
%23-32：uf1-uf10
%33-42：cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
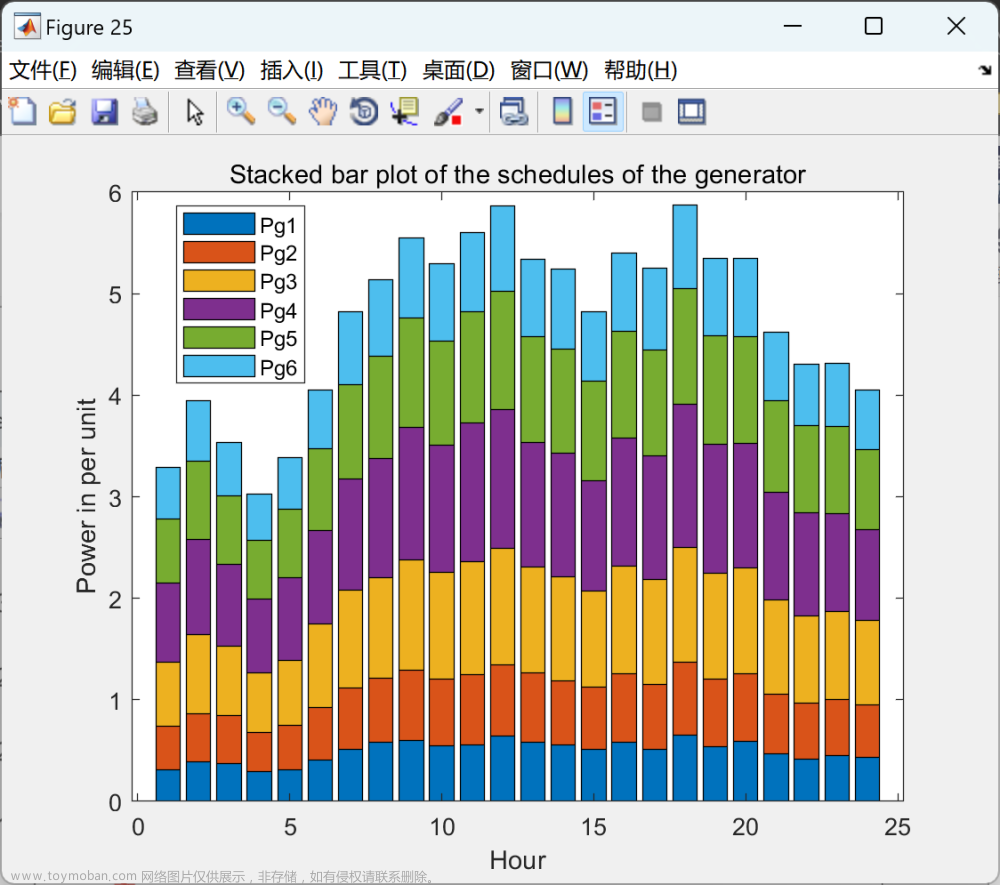
%47 盘式制动器设计 温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22):102-109.
%%
TestProblem=1;%1-47
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100;        % Population size
params.Nr = 200;        % Repository size
params.maxgen=200;    % Maximum number of generations
numOfObj=MultiObj.numOfObj;%目标函数个数
D=MultiObj.nVar;%维度
f = NSOOA(params,MultiObj);
X=f(:,1:D);%PS
Obtained_Pareto=f(:,D+1:D+numOfObj);%PF
if(isfield(MultiObj,'truePF'))%判断是否有参考的PF
True_Pareto=MultiObj.truePF;
%%  Metric Value
% ResultData的值分别是IGD、GD、HV、Spacing  (HV越大越好，其他指标越小越好)
ResultData=[IGD(Obtained_Pareto,True_Pareto),GD(Obtained_Pareto,True_Pareto),HV(Obtained_Pareto,True_Pareto),Spacing(Obtained_Pareto)];
else
    %计算每个算法的Spacing，Spacing越小说明解集分布越均匀
    ResultData=Spacing(Obtained_Pareto);%计算的Spacing
end
%%
disp('Repository fitness values are stored in Obtained_Pareto');
disp('Repository particles positions are store in X');

（2）部分结果

多目标优化算法：基于非支配排序的鱼鹰优化算法（NSOOA）MATLAB,MATLAB,优化算法,算法,matlab,数据结构

三、完整MATLAB代码

文件夹内包含NSOOA求解46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）的完整MATLAB，通过IGD，GD，HV，SP四种评价指标。

多目标优化算法：基于非支配排序的鱼鹰优化算法（NSOOA）MATLAB,MATLAB,优化算法,算法,matlab,数据结构文章来源地址https://www.toymoban.com/news/detail-806081.html