MCM备赛笔记——层次分析法-Toy模板网

这篇具有很好参考价值的文章主要介绍了MCM备赛笔记——层次分析法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

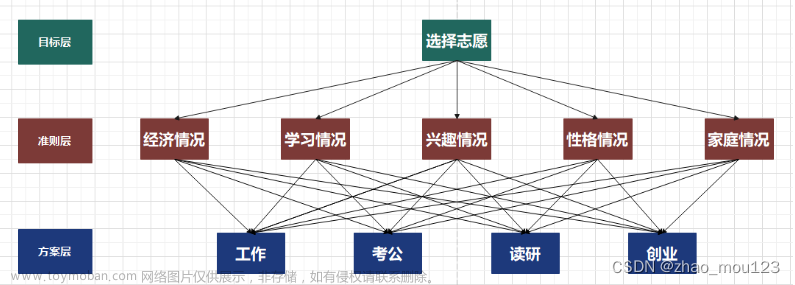
层次分析法

Key Concept 层次分析法（Analytic Hierarchy Process, AHP）是一种结构化的、定量化的决策方法，用于处理复杂的决策问题。它通过建立层次结构模型，将复杂问题分解为更小的部分（即准则、子准则和备选方案），然后通过成对比较和权重赋予来评估这些部分的相对重要性。

Key Concept Explanation 层次分析法的基本步骤包括：

建立层次结构模型：将决策问题分解为目标、准则、子准则和备选方案几个层次。
进行成对比较：在每个准则下，将备选方案或子准则两两进行比较，并根据相对重要性赋予1-9的标度值。
计算权重和一致性检验：利用成对比较矩阵计算出各因素的相对权重，并进行一致性检验以确保判断的合理性。一致性比率（CR）小于0.1通常被认为是可接受的。
合成总排序：根据各层次之间的关系，综合各因素权重，得出最终的决策结果

一.比较矩阵的构建

步骤 1：确定评价因素 首先，明确你需要比较的因素。例如，在选择最佳汽车时，评价因素可能包括成本、舒适度、品牌等。

步骤 2：建立矩阵 为这些因素创建一个方阵。如果你有 n 个因素，那么矩阵将是 n x n 的。矩阵的行和列分别代表同一组因素。

步骤 3：进行成对比较 对于矩阵中的每一对因素，决策者需要判断它们相对于决策目标的重要性。通常使用1到9的标度进行评分，其中1表示两因素同等重要，9表示一个因素比另一个因素极为重要。矩阵的对角线元素自然为1，因为它们是因素与自身的比较。

步骤 4：填充矩阵 如果元素 (i, j) 被赋值为 a，表示第 i 个因素比第 j 个因素重要 a 倍，那么其对称元素 (j, i) 应该被赋值为 1/a，表示第 j 个因素比第 i 个因素重要的程度。

MCM备赛笔记——层次分析法,数学建模,数学建模

二.一致性检验

在层次分析法（AHP）中，一致性检验是用来评估成对比较矩阵判断一致性的重要步骤。以下是进行一致性检验的步骤：

步骤 1：计算最大特征值（λmax） 首先，计算成对比较矩阵的最大特征值（λmax）。这通常通过求解矩阵的特征方程来完成，但在实际应用中，可以采用一种简化的方法：利用成对比较矩阵和它对应的权重向量相乘，然后将得到的向量的每个元素除以其相应的权重，最后取这些商的平均值作为λmax的估计。

MCM备赛笔记——层次分析法,数学建模,数学建模

步骤 2：计算一致性指标（CI） 使用公式 CI = (λmax - n) / (n - 1) 来计算一致性指标（CI），其中 n 是矩阵的阶数。CI值越小，表明成对比较的一致性越好。

MCM备赛笔记——层次分析法,数学建模,数学建模

步骤 3：确定随机一致性指标（RI） 随机一致性指标（RI）是针对随机成对比较矩阵的平均一致性指标值。这个值是预先确定的，取决于矩阵的阶数。

MCM备赛笔记——层次分析法,数学建模,数学建模

步骤 4：计算一致性比率（CR） 一致性比率（CR）是通过 CI 除以相应的 RI 来计算的，即 CR = CI / RI。这个比率用来评估矩阵的一致性水平。 MCM备赛笔记——层次分析法,数学建模,数学建模

步骤 5：评估一致性 如果 CR 小于或等于 0.1，通常认为成对比较的一致性是可以接受的。如果 CR 大于 0.1，则需要重新评估和修改成对比较矩阵，以提高其一致性。

MCM备赛笔记——层次分析法,数学建模,数学建模

三.求各个因素的权重

这里我们有三种求权重的方法，最后通过三种方法求得的权重向量其实基本上是一样的。

这里的权重指的是不同影响因素的影响权重。通过对应的权重向量乘以相应的数值向量就可以得到相应的判断评分。

1.算数平均数法求权重

平均数法是一种简单直观的求权重的方法，尤其适用于处理成对比较矩阵。以下是使用算术平均数法求权重的步骤：

MCM备赛笔记——层次分析法,数学建模,数学建模

计算每列的平均值，然后归一化。我们可以用代码来完成这个计算。

MCM备赛笔记——层次分析法,数学建模,数学建模

计算得到的归一化权重如下：

第一个因素的权重约为 0.5714
第二个因素的权重约为 0.2857
第三个因素的权重约为 0.1429

这些权重反映了每个因素相对于其他因素的重要性。在此例中，第一个因素是最重要的，第三个因素是最不重要的。 MCM备赛笔记——层次分析法,数学建模,数学建模

2.几何平均法求权重

MCM备赛笔记——层次分析法,数学建模,数学建模

通过几何平均法求权重得到

MCM备赛笔记——层次分析法,数学建模,数学建模

计算得到的归一化权重如下：

第一个因素的权重约为 0.5714
第二个因素的权重约为 0.2857
第三个因素的权重约为 0.1429

代码最后得到的权重向量大致是 [0.5714, 0.2857, 0.1429]，这反映了在成对比较矩阵中，第一个因素的重要性是最高的，第三个因素的重要性是最低的

3.特征值法求权重

这种方法是对一致矩阵的最大特征值对应的特征向量进行归一化

MCM备赛笔记——层次分析法,数学建模,数学建模

通过特征值法求他的权重

MCM备赛笔记——层次分析法,数学建模,数学建模

计算得到的归一化权重如下：

第一个因素的权重约为 0.5714
第二个因素的权重约为 0.2857
第三个因素的权重约为 0.1429

代码最后得到的权重向量大致是 [0.5714, 0.2857, 0.1429]，这反映了在成对比较矩阵中，第一个因素的重要性是最高的，第三个因素的重要性是最低的

四.求评分

在层次分析法（AHP）中，求最终评分的步骤通常涉及将各级准则对于目标层的权重与各备选方案对于这些准则的权重进行综合。以下是详细步骤：

步骤 1：确定各级准则的权重 使用之前讨论的方法（如成对比较矩阵的特征向量法、几何平均数法等）来确定决策目标下各准则的相对权重。

步骤 2：确定各备选方案相对于各准则的评分 对于每个准则，再次建立成对比较矩阵，比较各备选方案之间的相对优劣，并计算出各备选方案相对于该准则的权重。

步骤 3：计算备选方案的综合评分 对每个备选方案，将其对于各准则的权重乘以准则对于目标层的权重，然后将这些乘积相加，得到该方案的综合评分。

步骤 4：评估和选择 比较各备选方案的综合评分，评分最高的方案就是最佳的选择。

MCM备赛笔记——层次分析法,数学建模,数学建模

代码实现

import numpy as np
#定义判断矩阵
A=np.array([[1,2,4],[1/2,1,2],[1/4,1/2,1]])
#计算判断矩阵的大小
n=A.shape[0]

#使用特征值法求解权重向量
    #计算判断矩阵的特征值和特征向量
eig_val,eig_vec=np.linalg.eig(A)
    #找到最大的特征值
Max_eig=max(eig_val)
    #找到最大特征值对应的特征向量
Max_eig_vec=eig_vec[:,np.argmax(eig_val)]
    #对特征向量进行归一化来计算权重
weights=Max_eig_vec/np.sum(Max_eig_vec)

#定义因素矩阵
B=np.array([[100,200,400],[1,2,3],[10,20,30]])
#计算因素矩阵的大小
m=B.shape[0]
#对因素矩阵的每一列进行归一化
Stand_B=B/np.sum(B,axis=0)
#将归一化的因素矩阵和权重向量相乘
result=np.dot(Stand_B,weights)
#得到的结果就是最终的评价得分
result

这里假设我们有三个备选方案，最后得到三个方案的综合评分

MCM备赛笔记——层次分析法,数学建模,数学建模