一.无符号数全加器
1.无符号数四位全加器原理:
先来看一位全加器:
| 加数A |
加数B |
结果 |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0(进位1) |
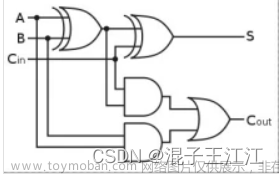
与异或门相似,用异或门记录

用与门记录A+B的进位

将进位输入与A+B结果相与再与进位相或得进位输出,将进位输入与加数相加计算结果

四位全加器则将低位的进位输出与高位的进位输入相连,最低位进位输入接地从而保证其仅为输入始终为0,溢出与否由最高位进位输出判断
2.电路及方案
将四个一位全加器相互连接,低位的进位输出与高位的进位输入相连,最低位进位输入接地从而保证其仅为输入始终为0,溢出与否由最高位进位输出判断

图表 1四位全加器电路图
3.verilog语言实现:
module full_adder(
input [3:0] a, b,
input cin,
output reg [3:0] cout,
output reg [3:0] sum ,
output [3:0] s,
output overflow);
integer i=0;
always@(*)
begin
for(i=0;i<=3;i=i+1)
if (i==0) begin
sum[i]=cin^a[i]^b[i];
cout[i]=a[i]&b[i]|cin&(a[i]^b[i]);
end
else begin
sum[i]=cout[i-1]^a[i]^b[i];
cout[i]=a[i]&b[i]|cout[i-1]&(a[i]^b[i]);
end
end
assign s=a+b;
assign overflow = ( a[3] & b[3] & ~s[3] ) | (~a[3] & ~b[3] & s[3]);
endmodule文章来源地址https://www.toymoban.com/news/detail-806413.html
RTL分析生成原理图

二.有符号数全加器
原理:有符号数则需要先判断符号位是否一致以及数的大小,当符号位不同时,需要将负数转补码再相通过一中的无符号数全加器相加,再将结果取补得原码;当符号位相同时,数值直接相加即可,同无符号数全加器,符号位取加数的符号位
至此,将无符号数全加器进行封装(如下图),根据原理通过HDL实现以上功能

verilog 行为描述:
module signed_adder
#(parameter WIDTH=4)
(
input wire [WIDTH-1:0] a,
input wire [WIDTH-1:0] b,
output reg [WIDTH-1:0] o_sum,
output reg [3:0] s,
output reg overflow
);
reg [WIDTH-1:0] o_a;
reg [WIDTH-1:0] o_b;
reg sign_a;
reg sign_b;
integer i=0;
always@(*)
begin
sign_a=a[WIDTH-1];
sign_b=b[WIDTH-1];
if(sign_a==sign_b==0) begin
o_sum=a+b;
s=a+b;
overflow = ( a[3] & b[3] & ~s[3] ) | (~a[3] & ~b[3] & s[3]);//溢出判断
end
else if(sign_a==sign_b==1) begin
o_a=(a^1)+1;
o_b=(b^1)+1;
o_sum=(a+b)^1;
s=a+b;
overflow = ( a[3] & b[3] & ~s[3] ) | (~a[3] & ~b[3] & s[3]);//溢出判断
end
else if(sign_a==0) begin
o_b=(b^1)+1;
o_sum=((a+b)^1)+1;
s=a+b;
overflow = ( a[3] & b[3] & ~s[3] ) | (~a[3] & ~b[3] & s[3]);//溢出判断
end
else begin
o_a=(a^1)+1;
o_sum=((a+b)^1)+1;
s=a+b;
overflow = ( a[3] & b[3] & ~s[3] ) | (~a[3] & ~b[3] & s[3]);//溢出判断
end
end文章来源:https://www.toymoban.com/news/detail-806413.html
endmodule
到了这里,关于用逻辑门实现四位加法器的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!