FPGA学习之实现PID算法

1 废话篇

1.1 理论学习

PID控制算法的学习，本次介绍位置式和增量式PID控制算法的原理和Matlab的仿真分析

1.1.1 模拟PID控制算法

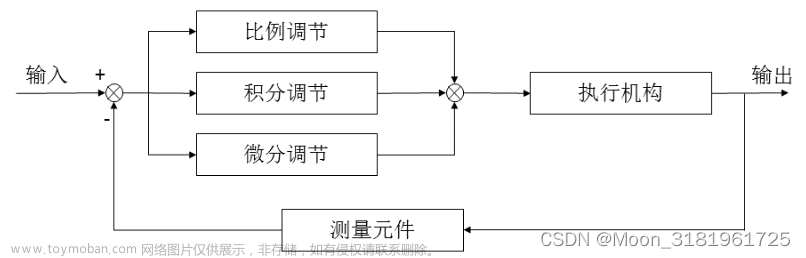
在工程中，比较用的多的就是比例、积分、微分控制，简称PID控制。G(s) 为被控对象的系统传递函数。

PID控制算法分为三种，分别是P调节，PI调节和PID调节算法。

P调节算法：比例控制是一种最简单的控制方式。其控制器的输出和输入误差信号成比例光系。偏差一旦产生。控制器立即就发生作用即调节控制输出，使被控量朝着减小误差的方向变化，偏差减小的速度取决于比例系数Kp，Kp越大偏差减小的越快，但是容易引起振荡，尤其是在迟滞环节比较大的情况下，Kp减小，发生振荡的可能性减小。但是调节的速度变慢。但单纯的比例控制存在稳态误差不能消除的缺点，这里就需要积分控制。P调节算法的控制规律和阶跃响应如下图所示

PI调节算法
在积分控制中，控制器的输出与输入误差信号的积分成正比关系。对一个自动控制系统，如果在进入问太后存在稳态误差，则称这个控制系统是有稳态误差的或者简称有差系统。为了消除稳态误差，在控制器中必须引入“积分项”。积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即便误差很小，积分项也会随着时间的增大而加大，它推动控制器的输出增大使稳态误差进一步减少，直至等于零。因此，比例+积分控制器，可以使系统进入稳态后无稳态误差，实质上就是对偏差累积进行控制，直至偏差为零。积分控制作用始终施加指向给定值的作用力，有利于消除静差，其效果不仅与偏差大小有关，而且还与偏差持续的时间有关。PI调节算法的控制规律和阶跃响应如下图所示：

PID调节算法：
在微分控制中，控制器的输出和输入误差信号的微分（即误差变化率）成正比关系。自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因使由于存在有较大惯性组件（环节）或有滞后组件，具有抑制误差的作用，其变化总是落后于误差的变化。解决的方法是使抑制误差的作用的变化“超前”，即在误差接近0时，抑制误差的作用就应该是零。这就是说，在控制器中仅引入“比例”项往往是不够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是 微分项，它能预测误差变化的趋势，这样，具有比例+微分的控制器，就能够提前使抑制误差的控制作用等于零，甚至为负值，从而避免了被控量的严重超调。所以对有较大惯性或者滞后的被控对象，微分比较有效果

1.1.2 离散化

1.1.3 伪算法

这里看到网上一个位置式PID实现的伪算法：

previous_error := 0 // 上一次偏差
integral := 0;   // 积分和

// 循环
// 采样周期为dt
loop：
	// setpoint 设定值
	// measured value 反馈值
	 error := setpoint - measured_value;    		 // 计算得到偏差
	 integral := integral + error * dt;     		 // 计算得到积分累加和
	 derivative := (error - previous_error ) / dt;   // 计算得到的微分
	 output := kp*error + ki*integral + kd*derivate;  // 计算得到PID的输出
	 previous_error := error;                         // 保存当前偏差为下一次采样时所需要的历史偏差
	 wait(dt);
	 goto loop;
	 

1.1.4 matlab算法位置式

对应的matlab仿真：

% 位置式PID算法仿真
clear;
clc;
%% 参数定义
Ts = 1e-3;% 采样时间     
e_sum = 0;% 多次误差和
% PID参数（可根据实际情况调节）
kp = 0.32;% 比例 
ki = 0.15;% 积分
kd = 0.12;% 微分
%% 建立被控系统
% 假设被控对象的系统传递函数为0.88/(0.05s + 1.5)
s_sys = tf(0.88,[0.05 1.5]); % 根据传递函数建立被控系统的模型
z_sys = c2d(s_sys,Ts,'z');    % 拉氏变换-->z变换
[m,n] = tfdata(z_sys,'v');
%% 开始PID控制
T = 2000;% 设置仿真运行时间
r = 800;% 期望输出值
% 预先分配内存
u = zeros(1,T);% PID输出初始值
y = zeros(1,T);% 被控系统响应输出
e = zeros(1,T);% 误差信号
for k=2:1:T
    y(k) = -n(2)*y(k-1) + m(1)*u(k) + m(2)*u(k-1);% 计算被控系统输出
    e(k) = r - y(k);   % 计算误差
    u(k) = kp*e(k) + ki*e_sum + kd*(e(k)-e(k-1)); %根据误差调整PID控制量输出
    e_sum = e_sum+e(k);% 计算多次误差和
end
% 绘制过渡过程的曲线
t = 1:1:T;
figure('Color','White');
plot(t,y,'r-','LineWidth',1.2);
title('pid-pos')
xlabel('t');
ylabel('y');
grid on;
set(gca,'FontSize',12,'LineWidth',1.2,'Fontname', 'Times New Roman','FontWeight','Bold')

1.1.5 matlab 算法增量式

% 位置式PID算法仿真
clear;
clc;
%% 参数定义
Ts = 1e-3;% 采样时间     
% PID参数（可根据实际情况调节）
kp = 0.32;% 比例 
ki = 0.15;% 积分
kd = 0.12;% 微分
%% 建立被控系统
% 假设被控对象的系统传递函数为0.88/(0.05s + 1.5)
s_sys = tf(0.88,[0.05 1.5]); % 根据传递函数建立被控系统的模型
z_sys = c2d(s_sys,Ts,'z');    % 拉氏变换-->z变换
[m,n] = tfdata(z_sys,'v');
%% 开始PID控制
T = 2000;% 设置仿真运行时间
r = 800;% 期望输出值
% 预先分配内存
u = zeros(1,T);% PID输出初始值
y = zeros(1,T);% 被控系统响应输出
e = zeros(1,T);% 误差信号
d_u = zeros(1,T);% PID输出增量
for k=3:1:T
    y(k) = -n(2)*y(k-1) + m(1)*u(k) + m(2)*u(k-1);% 计算被控系统输出
    e(k) = r - y(k);   % 计算误差
    d_u(k) = kp*(e(k)-e(k-1))+ki*e(k)+kd*((e(k)-e(k-1))-(e(k-1)-e(k-2)));% 根据误差获取PID增量
    u(k) = u(k-1) + d_u(k);% 根据PID增量计算PID控制输出
end
% 绘制过渡过程的曲线
t = 1:1:T;
figure('Color','White');
plot(t,y,'r-','LineWidth',1.2);
title('pid-incre')
xlabel('t');
ylabel('y');
grid on;
set(gca,'FontSize',12,'LineWidth',1.2,'Fontname', 'Times New Roman','FontWeight','Bold')

1.1.5 verilog 实现PID

error.v

module error(

    input clk,
    input rst_n,
    input signed [9:0] target,
    input signed [9:0] y,
    
    output signed [9:0] ek0,
    output reg signed[9:0] ek1;
    output reg signed [9:0] ek2;
);

assign ek0 = target - y;   // 计算e(k)

always @(posedge clk or negedge rst_n) begin
    
    if(!rst_n) begin
        ek1 <= 10'd0;
        ek2 <= 10'd0;
    end
    else begin
        ek1 <= ek0;                 // 延时一个时钟周期 得到e(k-1)
        ek2 <= ek1;                 // 再延时一个时钟周期 得到e(k-2)
    end 
end


endmodule

pid_value.v

///
// Company: <Name>
//
// File: pid_value.v
// File history:
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//
// Description: 
//
// <Description here>
//
// Targeted device: <Family::SmartFusion> <Die::A2F060M3E> <Package::288 CS>
// Author: <Name>
//
/// 

//`timescale <time_units> / <precision>

module pid_value( 

    input clk,                          // 时钟信号
    input rst_n,                        // 复位信号，低电平有效
    input signed [14:0] d_uk,           // pid 增量

    output reg signed [14:0] uk0        // pid 输出值

);

reg signed [14:0] uk1 = 15'd0;          // 上一时刻u(k-1) 的值

always @(d_uk) begin
    uk0 = uk1 + d_uk;                   // 计算pid 输出值
    uk1 = uk0;                          // 寄存上一时刻 u(k-1) 的值
end

//<statements>

endmodule

incre_value.v

///
// Company: <Name>
//
// File: incre_value.v
// File history:
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//
// Description: 
//
// <Description here>
//
// Targeted device: <Family::SmartFusion> <Die::A2F060M3E> <Package::288 CS>
// Author: <Name>
//
/// 

//`timescale <time_units> / <precision>

module incre_value( 

    input signed [9:0] ek0,
    input signed [9:0] ek1,
    input signed [9:0] ek2,

    input [3:0] kp,
    input [3:0] ki,
    input [3:0] kd,

    output signed [14:0] d_uk

);


assign  d_uk = kp*(ek0 -ek1) + ki*ek0 + kd*((ek0 - ek1)-(ek1 - ek2)); // 计算pid增量

//<statements>

endmodule

demo_top.v

///
// Company: <Name>
//
// File: demo_top.v
// File history:
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//
// Description: 
//
// <Description here>
//
// Targeted device: <Family::SmartFusion> <Die::A2F060M3E> <Package::288 CS>
// Author: <Name>
//
/// 

//`timescale <time_units> / <precision>

module demo_top (

    input clk,                          // 时钟信号
    input rst_n,                        // 复位信号
    input signed [9:0] target,          // 目标值
    input signed [9:0] y,               // 实际输出值

    input [3:0] kp,
    input [3:0] ki,
    input [3:0] kd,
    
    output signed [14:0] uk0            // pid 输出值
);


wire signed [9:0] ek0;
wire signed [9:0] ek1;
wire signed [9:0] ek2;

error error_inst(
    .clk(clk),
    .rst_n(rst_n),
    .y(y),
    .ek0(ek0),
    .ek1(ek1),
    .ek2(ek2)
);

wire signed [14:0] d_uk; // pid 增量
incre_value incre_value_inst(

    .ek0(ek0),
    .ek1(ek1),
    .ek2(ek2),
    .kp(kp),
    .ki(ki),
    .kd(kd),
    .d_uk(d_uk)

);

pid_value pid_value_inst(

    .clk(clk),
    .rst_n(rst_n),
    .d_uk(d_uk),
    .uk0(uk0)
);

endmodule

tb_demo_top.v文章来源地址https://www.toymoban.com/news/detail-806803.html

///
// Company: <Name>
//
// File: tb_demo_top.v
// File history:
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//      <Revision number>: <Date>: <Comments>
//
// Description: 
//
// <Description here>
//
// Targeted device: <Family::SmartFusion> <Die::A2F060M3E> <Package::288 CS>
// Author: <Name>
//
/// 

//`timescale <time_units> / <precision>

module tb_demo_top();

reg clk;
reg rst_n;
reg signed [9:0] target ;  // 目标值
reg signed [9:0] y; // 实际值

reg [3:0] kp;    // 比例系数
reg [3:0] ki;    // 积分系数
reg [3:0] kd;    // 微分系数

wire signed [14:0] uk0;

reg [10:0] i;
reg [8:0] mytxt[0:1997];

initial begin
    $readmemh(,mytxt);
    clk = 1'b0;
    rst_n = 1'b1;
    #5 rst_n = 1'b0;
    #5 rst_n = 1'b1;
    target = 10'd350;
    kp = 4'd10;
    ki = 4'd9;
    kd = 4'd8;

    for(i = 0; i<11'd1997; i=i+1)
        begin
            y = mytxt[i];
            #10;
        end
end

 
always #5 clk = ~clk;

demo_top demo_top_tb(.clk(clk),
.rst_n(rst_n),
.target(target),
.y(y),
.kp(kp),
.ki(ki),
.kd(kd),
.uk0(uk0)
); 

//<statements>

endmodule

到了这里，关于FPGA学习之实现PID算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！