显著性检验【t-test、方差分析、ks检验】-Toy模板网

这篇具有很好参考价值的文章主要介绍了显著性检验【t-test、方差分析、ks检验】。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

显著性检验【t-test、方差分析、ks检验】

0、目录

1显著性检验基本定义（what？）

2.使用显著性检验的意义（why? ）

3.显著性检验的具体操作流程（how? ）

1、显著性检验基本定义

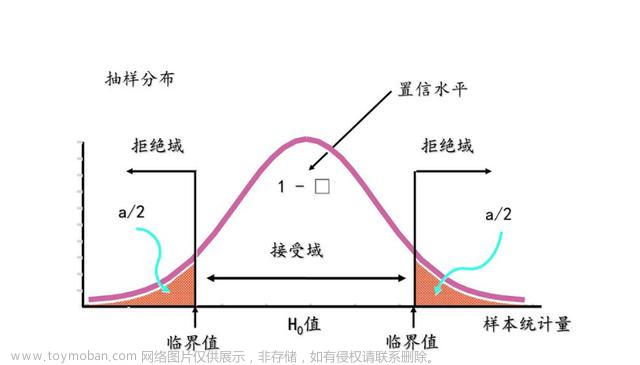
统计假设检验（Statistical hypothesis testing）
- 事先对总体（随机变量）的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设是否合理
显著性检验（significance test）
- 统计假设检验的一种
- 显著性检验是用于检测科学实验中实验组与对照组之间是否有差异以及差异是否显著的办法。
在使用显著性检验之前必须先进行统计假设，也就是无效假设/零假设/原假设
无效假设/零假设/原假设（null hypothesis）
- 数据结果之间本身不存在显著性差异
- 指进行统计检验时预先建立的假设。零假设成立时，有关统计量应服从已知的某种概率分布。
- 当统计量的计算值落入否定域时，可知发生了小概率事件，应否定原假设。
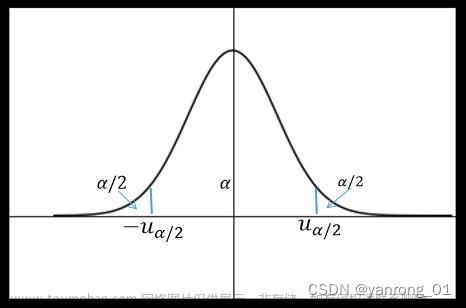
若原假设为真，而检验的结论却劝你放弃原假设。此时，我们把这种错误称之为第一类错误。通常把第一类错误出现的概率记为α
若原假设不真，而检验的结论却劝你采纳原假设。此时，我们把这种错误称之为第二类错误。通常把第二类错误出现的概率记为β
通常只限定犯第一类错误的最大概率α, 不考虑犯第二类错误的概率β。我们把这样的假设检验称为显著性检验，概率α称为显著性水平。

2.使用显著性检验的意义

实例讲解
- 一个球迷想要评价c罗和梅西的网络影响力，下列分别为二人在2017年每月社交网络发布后获得的点赞量/评论量，想要知道二人是否有存在明显的差异
- CR7= {23,25,26,27,23,24,22,23,25,29,30,32}
- Messi= {24,25,23,26,27,25,25,28,30,31,29,28}
- 根据零假设的定义，作出“两人的点赞量没有显著差异”的假设，最后计算得出，方差检验的p_value= 0.459，那也就意味着两人的点赞量并没有明显的差异

3、显著性检验的具体操作流程

方差分析

方差分析(Analysis of Variance,简称ANOVA),又称“变异数分析”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验
在显著性水平α =0.05的情况下，p>0.05接受原假设，p值＜0.05拒绝原假设
原假设是二人间不存在显著性差异，由于p=0.459＞0.05，所以接受原假设，即二人间不存在显著性差异
如果这里的p值小于0.05，那么就要拒绝原假设，即二人间存在显著性差异

p_value的另一种理解

实例中的p_value=0.459，意思就是说偶然因素导致数据发生这种差异的概率是0.459，跟0.05一比大好多。那么就是说偶然因素很有可能导致了这种差异，所以数据本身之间是不存在差异的。

'''

 方差齐性检验  在显著性水平α =0.05的情况下，p>0.05接受原假设, 所以接受原假设，即样本集B和样本集H间不存在显著性差异

'''

from scipy import stats  # 导入相应模块

v3=[23,25,26,27,23,24,22,23,25,29,30,32]
v4=[24,25,23,26,27,25,25,28,30,31,29,28]

stats.levene(v3,v4, center="mean")
fVal, pSD = stats.levene(v3,v4, center="mean")

print("ANOVA-0",fVal, pSD)

输出结果：
0.5671069450362157
0.45939425229350794

T 检验（T-Test）

T 检验用于确定两个变量的均值之间是否存在显著差异，并判断它们是否属于同一分布
双尾测试
函数 ttest_ind() 获取两个相同大小的样本，并生成 t 统计和 p 值的元组

查找给定值 v1 和 v2 是否来自相同的分布：

'''

 T-test 在显著性水平α =0.05的情况下，p>0.05接受原假设, 所以接受原假设，即样本集B和样本集H间不存在显著性差异

'''

v3=[23,25,26,27,23,24,22,23,25,29,30,32]
v4=[24,25,23,26,27,25,25,28,30,31,29,28]

import numpy as np
from scipy.stats import ttest_ind
from scipy import stats

res = ttest_ind(v3, v4)
print（res）

输出结果
Ttest_indResult(statistic=-0.8599394154935148, pvalue=0.3990967787539713)

KS 检验

KS 检验用于检查给定值是否符合分布
该函数接收两个参数；测试的值和 CDF
- CDF 为累积分布函数(Cumulative Distribution Function)，又叫分布函数。CDF 可以是字符串，也可以是返回概率的可调用函数。
可以用作单尾或双尾测试，默认情况下它是双尾测试。我们可以将参数替代作为两侧、小于或大于其中之一的字符串传递。
查找给定值是否符合正态分布
```
import numpy as np
from scipy.stats import kstest
 
v = np.random.normal(size=100)
 
res = kstest(v, 'norm')
 
print(res)
```
输出结果
KstestResult
(statistic=0.047798701221956841, pvalue=0.97630967161777515)文章来源地址https://www.toymoban.com/news/detail-806908.html