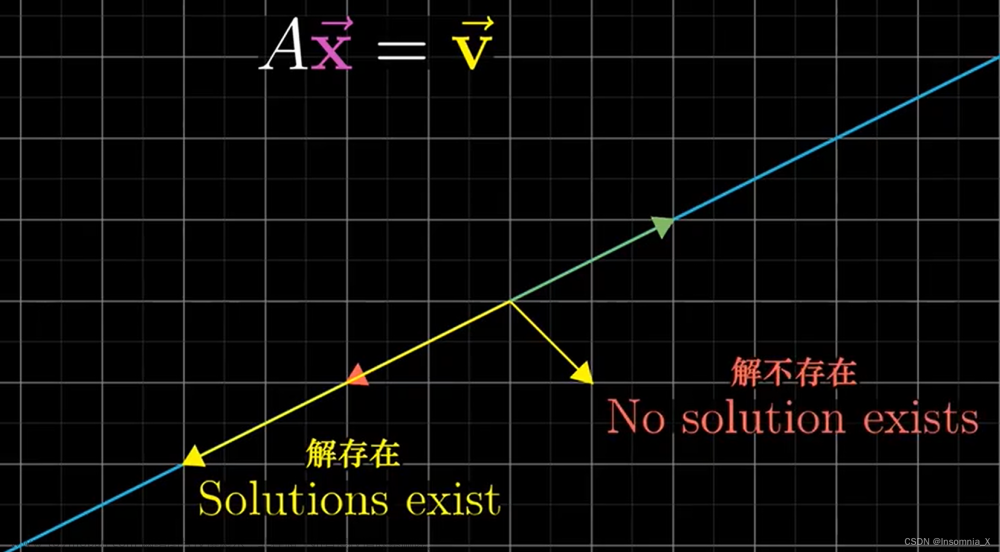
线性代数:齐次线性方程组学习笔记
一、定义
齐次线性方程组是指所有方程的常数项均为零的线性方程组,即形如 A x = 0 Ax=0 Ax=0 的方程组。
其中,矩阵 A A A 是一个 m × n m \times n m×n 的矩阵,向量 x x x 是一个 n n n 维列向量, 0 \mathbf{0} 0 是一个 m m m 维零向量。
二、性质
齐次线性方程组有以下性质:
1. 性质1
齐次线性方程组的解集合是一个子空间。
2. 性质2
如果齐次线性方程组有非零解,则它有无穷多个解。
3. 性质3
如果矩阵 A A A 的秩等于 n n n,则齐次线性方程组仅有零解。
4. 性质4
对于任意的 m × n m \times n m×n 矩阵 A A A 和任意的 n n n 维列向量 b b b,其增广矩阵 [ A b ] \begin{bmatrix} A & b \end{bmatrix} [Ab] 的秩等于矩阵 A A A 的秩或者比矩阵 A A A 的秩小 1 1 1。
三、求解
对于齐次线性方程组 A x = 0 Ax=0 Ax=0,我们可以通过以下步骤求解:
1. 构造增广矩阵
将矩阵 A A A 和零向量 0 \mathbf{0} 0 拼接成一个 m × ( n + 1 ) m \times (n+1) m×(n+1) 的增广矩阵 [ A 0 ] \begin{bmatrix} A & \mathbf{0} \end{bmatrix} [A0]。
2. 高斯消元
对增广矩阵进行高斯消元,化为阶梯形矩阵或行最简形矩阵。
3. 求解基础解系
如果阶梯形矩阵或行最简形矩阵中存在形如 [ 0 1 a 1 a 2 ⋯ a n − k ] \begin{bmatrix} \mathbf{0} & 1 & a_1 & a_2 & \cdots & a_{n-k} \end{bmatrix} [01a1a2⋯an−k] 的行,则 x k + 1 = − a 1 x k + 2 − a 2 x k + 3 − ⋯ − a n − k x n x_{k+1}=-a_1 x_{k+2}-a_2 x_{k+3}-\cdots-a_{n-k} x_n xk+1=−a1xk+2−a2xk+3−⋯−an−kxn,其中 x k + 2 , x k + 3 , … , x n x_{k+2},x_{k+3},\ldots,x_n xk+2,xk+3,…,xn 是自由变量。因此,齐次线性方程组的通解为
x = c 1 v 1 + c 2 v 2 + ⋯ + c k v k x=c_1 \mathbf{v}_1 + c_2 \mathbf{v}_2 + \cdots + c_k \mathbf{v}_k x=c1v1+c2v2+⋯+ckvk
其中, v 1 , v 2 , … , v k \mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_k v1,v2,…,vk 是矩阵 A A A 的基础解系, c 1 , c 2 , … , c k c_1,c_2,\ldots,c_k c1,c2,…,ck 是任意常数。
如果阶梯形矩阵或行最简形矩阵中不存在自由变量,则齐次线性方程组的唯一解为零解。文章来源:https://www.toymoban.com/news/detail-806959.html
四、应用
齐次线性方程组在计算机图形学、数据降维和机器学习等领域有着广泛的应用。例如:文章来源地址https://www.toymoban.com/news/detail-806959.html
- 计算机图形学:用于计算旋转、缩放、平移等几何变换矩阵。
- 数据降维:用于通过主成分分析等方法对高维数据进行降维。
- 机器学习:用于求解线性回归、逻辑回归等模型参数。
到了这里,关于线性代数:齐次线性方程组学习笔记的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!