用Go plan9汇编实现斐波那契数列计算-Toy模板网

这篇具有很好参考价值的文章主要介绍了用Go plan9汇编实现斐波那契数列计算。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

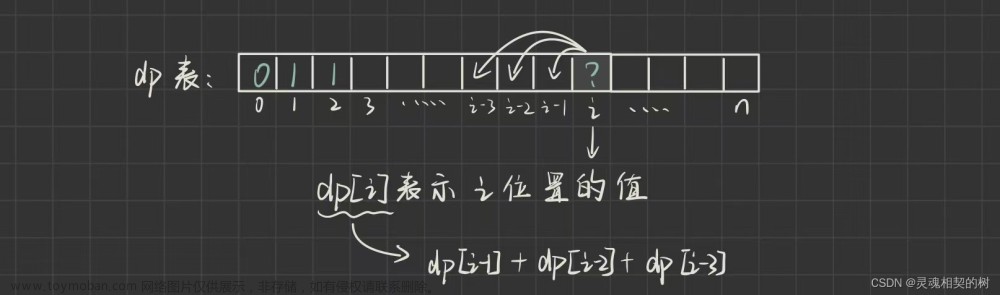
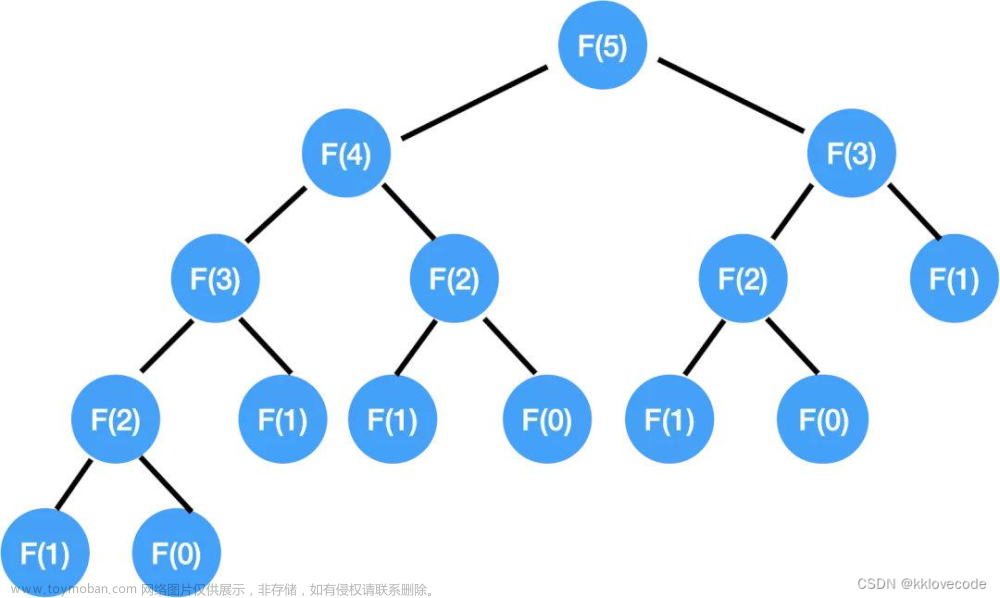
斐波那契数列是一个满足递推关系的数列，如：1 1 2 3 5 8 ...
其前两项为1，第3项开始，每一项都是其前两项之和。
用Go实现一个简单的斐波那契计算逻辑

func fib(n int) int {
	if n == 1 || n == 2 {
		return 1
	}
	return fib(n-1) + fib(n-2)
}

我们将其改进一下，用更简单的方式描述，同时把变量的定义提到前边，并将返回的逻辑拿到函数末尾。

func fib1(n int) int {
	var tmp, res, res1, res2 int
	if n == 1 {
		goto return1
	}
	if n == 2 {
		goto return1
	}
	tmp = n - 1
	res1 = fib1(tmp)
	tmp = n - 2
	res2 = fib1(tmp)
	res = res1 + res2
	return res
return1:
	return 1
}

继续改进

func fib2(n int) int {
	var tmp, res, res1, res2 int
	if n == 1 {
		goto return1
	}
	if n == 2 {
		goto return1
	}
	tmp = n
	tmp -= 1
	res1 = fib2(tmp)
	tmp = n
	tmp -= 2
	res2 = fib2(tmp)
	res = res1
	res += res2
	return res
return1:
	return 1
}

继续改进，复用变量

func fib3(n int) int {
	var res, res1 int
	if n == 1 {
		goto return1
	}
	if n == 2 {
		goto return1
	}
	res1 = n
	res1 -= 1
	res = fib3(res1)
	res1 = n
	res1 -= 2
	res1 = fib3(res1)
	res += res1
	return res
return1:
	return 1
}

继续改进

func fib4(r0 int) int {
	var r1, r2 int
	if r0 <= 2 {
		goto return1
	}
	r2 = r0
	r2 -= 1
	r1 = fib4(r2)
	r2 = r0
	r2 -= 2
	r2 = fib4(r2)
	r1 += r2
	return r1
return1:
	return 1
}

汇编函数接口定义

func fib5(n int) int

汇编函数实现

TEXT ·fib5(SB),$40-16
    MOVD R0, tmp-24(SP);MOVD R1, tmp-16(SP);MOVD R2, tmp-8(SP) // save context
    MOVD n+0(FP), R0; MOVD $0, R1; MOVD $0, R2 // R0: load value from stack memory
    CMP $2, R0; BLE LABEL_RETURN1 // if R0 <= 2 {goto LABEL_RETURN1}
    MOVD R0, R1; SUB $1,  R1 // R1 = R0 - 1
    MOVD R1, tmp-40(SP); CALL ·fib5(SB); MOVD tmp-32(SP), R1 // R1 = fib5(R1)
    MOVD R0, R2; SUB  $2, R2 // R2 = R0 - 2
    MOVD R2, tmp-40(SP); CALL ·fib5(SB); MOVD tmp-32(SP), R2 // R2 = fib5(R2)
    ADD R1, R2; MOVD R2, R0 // R0 = R1 + R2
    JMP LABEL_END
LABEL_RETURN1:
    MOVD $1, R0 // R0 = 1
LABEL_END:
    MOVD R0, n+8(FP) // set return value: R0
    MOVD tmp-24(SP), R0; MOVD tmp-16(SP), R1; MOVD tmp-8(SP),  R2 // recovery context
    RET