线性矩阵不等式（LMI）（一）：简单介绍

线性矩阵不等式（LMI）（一）：简单介绍

主要从以下三个方面介绍：

1. 什么是线性矩阵不等式(LMI)
2. 为什么要用线性矩阵不等式(LMI)
3. 线性矩阵不等式的发展（控制系统中）

1. 线性矩阵不等式

如名字所示线性矩阵不等式三要素为：

• 线性 - 注意双线性时，LMI不好求解(非凸问题)；例：在不等式中出现$PAK$形式，其中$P,K$都为未知变量；可以利用消元法/换元法[1]转化为LMI形式；
• 矩阵变量 - 可以表示成一般形式/标准形式；
• 不等号 - 表示矩阵的正定/负定，而不是大小关系；

1.1 一般形式

• LMI的一般形式可以表示为[2]：
  $$L(X)=D^{T}X+X^{T}D+\sum _{i=1}^l(E_i^{T}X{F}_i+F_i^T{X}^T{E}_i)+Q<0$$
  其中，$X^{n\times n}\in {\mathbb{R}}^{m\times n}$是矩阵变量，$D,E_i\in {\mathbb{R}}^{m\times n},F_i\in {\mathbb{R}}^{n\times n},i=1,2,\dots ,l.$ 是任意矩阵， $Q\in {\mathbb{S}}^n$是对称矩阵。

  式中， $D^{T}X+X^{T}D,E_i^{T}X{F}_i+F_i^T{X}^T{E}_i,Q$保证了$L(X)$的线性和对称性；通过选择合适的矩阵$X$使得$L(X)$是负定的。

  • 当$X=P=P^T,D=A,F_i=E_i=0$时，LMI一般形式可以转化为Lyapunov LMI：
    $$L(P)=A^{T}P+P^{T}A+Q<0$$

    对于控制系统来说，当存在一个正定矩阵$P$，使得上式成立时，则系统时稳定的。

    Lyapunov LMI的最初解法为，通过选择调整正定矩阵$Q$，求解Lyapunov方程$A^{T}P+PA=-Q$来求解矩阵$P$;

1.2 标准形式

• LMI的标准形式为[2]:
  $$A(x)=A_0+x_1{A}_1+\cdot \cdot \cdot +x_n{A}_n<0$$
  其中，$x_i,i=1,2,\dots ,n$是未知标量，称为决策变量。$A_i,i=1,2,\dots ,n$是已知对称矩阵。

  选择标量$x_i$使得上式成立；

  • 例： 让$x_1,x_2\in \mathbb{R}$,
    $$A\left(x\right)=A_0+A_1{x}_1+A_2{x}_2,$$
    其中，$A_0=\left[\begin{array}{ccc}1& & 0\\ 0& & -1\end{array}\right],A_1=\left[\begin{array}{ccc}-1& & -1\\ -1& & 4\end{array}\right],A_2=\left[\begin{array}{ccc}-1& & 1\\ 1& & -2\end{array}\right].$

    带入可得
    $$A\left(x\right)=\left[\begin{array}{cc}1-x_1-x_2& -x_1+x_2\\ -x_1+x_2& -1+4x_1-2x_2\end{array}\right],$$
    $A(x)<0$等价于
    $$\{\begin{array}{l}1-x_1-x_2<0,\\ \det \left[\begin{array}{cc}1-x_1-x_2& -x_1+x_2\\ -x_1+x_2& -1+4x_1-2x_2\end{array}\right]=-5x_1^2+5x_1+x_2^2-x_2-1>0.\end{array}$$

    $$\{\begin{array}{l}-1+x_1+x_2>0\\ \left(x_2-\sqrt{5}{x}_1+\frac{\sqrt{5}-1}{2}\right)\left(x_2+\sqrt{5}{x}_1-\frac{\sqrt{5}+1}{2}\right)>0.\end{array}$$

    根据上式可得$(x_1,x_2)$取值范围为，下图所示公共部分。
    

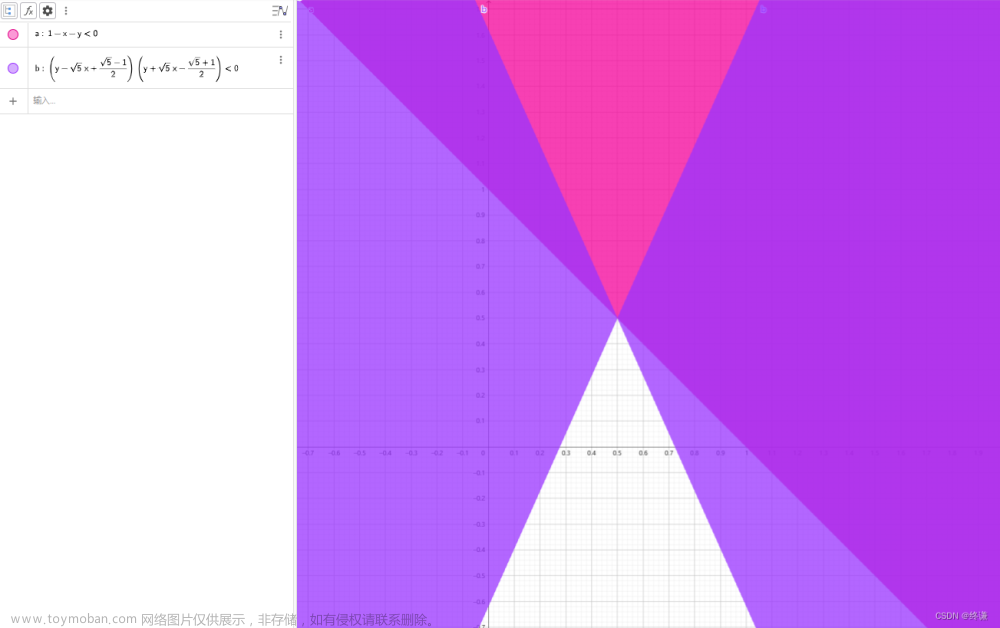
1.3 二者关系

• 让标准形式中$A_i,i=1,...,n$ 为一般形式中$P$的基底，则$P$可表示为$P=A_0+x_1{A}_1+\cdot \cdot \cdot +x_n{A}_n$。定义$T_i=A^T{A}_i+A_i^{T}A，$带入到标准形式中，则可将一般形式转化为标准形式
  $$L(P)=T_0+\sum _{i=1}^n{x}_i{T}_i$$

  • 例：根据Lyapunov稳定理论，二维线性系统
    $$\dot{x}(t)=Ax(t),x(0)\ne 0$$
    稳定的充要条件是，存在满足不等式
    $$A^{T}P+PA<0$$
    的正定阵$P=P^T\in {\mathbb{R}}^{2\times 2}$。这里，2 × 2的对称阵$P$有以下对称基底
    $$P_1=[\begin{array}{cc}1& 0\\ 0& 0\end{array}],P_2=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],P_3=\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$$
    通过利用这些对称基底，*$P$*可写为
    $$P=[\begin{array}{cc}{x}_1& x_2\\ x_2& x_3\end{array}]=x_1{P}_1+x_2{P}_2+x_3{P}_3$$
    将其带入(6)可得
    $$AP+P{A}^T=x_1(A{P}_1+P_1{A}^T)+x_2(A{P}_2+P_2{A}^T)+x_3(A{P}_3+P_3{A}^T)<0$$

2. 线性矩阵不等式的优点

在分析与设计控制系统中的优点[2]

• 全局优化解及数值可靠性

  • LMIs 的形式是一种凸约束形式，因此有全局最优解
  • 可以得到可靠和有效的数值解
  • 规模很大也可以求解

• 能够进行系统的多目标设计

  • 通过将系统不同性能要求，转化为LMI组形式，共同求解LMIs，实现系统多目标设计

• 成熟的工具包可以使用

  • MATLAB LMI toolbox；（后面介绍这个）
  • YALMIP;（可以参考文献[3]）
  • CVX;（没用过不太清楚）

数值可靠性重要性！

• 数值可靠性可分为

  • good-conditioned problems （e.g. 奇异值分解），无论怎么分解都可以保证数值的精度。
  • ill-conditioned problems （e.g. 矩阵求逆），矩阵求逆，如果条件数很大，求的矩阵的逆精度会受到损失。

• 例:给定以下单输入基准系统
  $$\dot{x}=Ax+Bu$$
  其中
  A = [ 20 20 19 ⋱ ⋱ 20 1 ] , B = [ 1 0 ⋮ 0 ] \left.A=\left[\begin{array}{ccccc}20&&&&\\20&19&&&\\&\ddots&\ddots&&\\&&20&1&\end{array}\right.\right],B=\left[\begin{array}{c}1\\0\\\vdots\\0\end{array}\right] A= ​2020​19⋱​⋱20​1​​ ​,B= ​10⋮0​ ​
  配置系统极点 $p=[-1\pm i,-2\pm i,-3\pm i,-4\pm i,-5\pm i,-6\pm i,-7\pm i,-8\pm i,-9\pm i,-10\pm i]$

  使用matlab place 命令得到的结果为：
  $$\begin{array}{rlrlrlr}& & \text{452.58+}\text{0i},& & \text{-3.5361+}\text{48.266i},& & \text{-3.5361}\text{48.266i}\\ & & \text{-7.8615+}\text{21.439i},& & \text{-7.8615-}\text{21.439i},& & -8.7621+\text{11.15i}\\ & & -8.7621-\text{11.15i},& & \text{-9.0799+}\text{4.9281i},& & \text{-9.0799-}\text{4.9281i}\\ & & \text{-9.1658+}\text{0i},& & \text{19+}\text{0i},& & \text{18+}\text{0i}\\ & & \text{17+}\text{0i},& & \text{16+}\text{0i},& & \text{15+}\text{0i}\\ & & \text{14+}\text{0i},& & \text{13+}\text{0i},& & \text{12+}\text{0i}\\ & & \text{11+}\text{0i}& & & & \end{array}$$
  从上可以看出place算法在一些时候并不能保证数值稳定性

2.1 LMI 是一个凸集

• 凸优化问题 = 凸指标+凸约束
  $$\{\begin{array}{l}\text{min}{f}_0(x)\\ \text{s.t.}{f}_i(x)\le 0,i=1,2,...,m\\ Ax=b\end{array}$$
  其中$f_i,i=0,1,...,m$是一组凸函数,等式约束必须是仿射结构(线性的)。

  目标函数，是凸函数；不等式约束是凸集；等式约束时仿射的；则称此优化问题为凸优化问题。

• 凸函数
  $$f(\theta x+(1-\theta )y)\le \theta f(x)+(1-\theta )f(y)$$
  其中，$\theta \in [0,1],x,y\in \Omega$,$\Omega$是一个凸集。

  简单描述，函数图像上任取两点连线的中点，大于此函数任取两点对应的自变量的中点的函数值，则此函数为凸函数。

• 凸集

  如果$x,y\in \mathbb{F}，0\le \theta \le 1$，且
  $$\theta x_1+(1-\theta )x_2\in \mathbb{F}$$
  则称$\mathbb{F}$是一个凸集。

  简单描述，集合中任取两点连成的线段，若线段上所有的点都包含的集合里面则集合是凸集。

• 含有LMI的优化问题
  { min   f 0 ( x ) s.t.   x ∈ { x ∣ A ( x ) < 0 } ∩ F \begin{cases} \text{min} ~~ f_0(x)\\ \text{s.t.} ~~ x\in \{x|A(x)<0\} \cap \mathbb{F} \end{cases} {min  f0​(x)s.t.  x∈{x∣A(x)<0}∩F​
  $A(x)<0$ 是LMI，且$\mathbb{F}$是一个凸集。

  • 当目标函数$f_0(x)$是凸函数时，此优化问题是凸优化问题；
    • $A(x)\le 0$是一个凸集（利用凸集定义可证明）。

• 涉及LMI的三个标准问题

  大多数问题都可以转化为标准问题

  • 可行性问题

    找到一个解$x\in {\mathbb{R}}^n$满足如下LMI:
    $$A(x)<B(x)$$

    当把$B(x)$移动到不等式左边，令$F_i=A_i-B_i,i=0,1,\mathrm{2...},n$,可以将上述LMI转化为标准LMI：$F(x)<0$;

    上述问题可以利用，MATLAB LMI Toolbox中 feasp 命令求解。

    feasp 求解的时以下的带有LMI的辅助凸优化问题
    $$\{\begin{array}{l}\text{min}t\\ \text{s.t.}A(x)<B(x)+tI\end{array}$$
    根据矩阵特征值特性${\lambda }_{\text{max}}(A)<t⟺A-tI<0$；上式表示为使得矩阵$A(x)-B(x)$的特征值全小于$t$，即矩阵为负定。因此，只有凸优化问题（22）$t<0$时，存在严格可行解$x$,使得矩阵$A(x)-B(x)<0$，使得$A(x)<B(x)$成立。

  • 凸最小化问题

    给一个凸函数$f(x)$，找到一个解$x\in {\mathbb{R}}^n$满足以下带有LMI约束的最小化问题
    $$\{\begin{array}{l}\text{min}f(x)\\ \text{s.t.}A(x)<B(x)\end{array}$$

    MATLAB LMI Toolbox中 mincx 命令求解
    $$\{\begin{array}{l}\text{min}{c}^{T}x\\ \text{s.t.}L(x)<R(x)\end{array}$$

  • 广义特征值问题

    找到以下最小化问题的解$x\in {\mathbb{R}}^n$
    $$\{\begin{array}{l}\text{min}\lambda \\ \text{s.t.}A(x)<\lambda B(x)\\ B(x)>0\\ C(x)>0\end{array}$$

    MATLAB LMI Toolbox中 gevp 命令求解

  mincx 和 gevp 区别？凸最小化问题和广义特征值问题区别？

3. 线性矩阵不等式的发展

• 播种期(1890)

  根源：求解一个正定矩阵$P$使得$A^{T}P+PA<0$成立，保证线性系统$\dot{x}(t)=Ax(t)$是渐进稳定的；

  解决方法：Lyapunov通过选择一个正定矩阵$Q$，通过求解Lyapunov方程$A^{T}P+PA=-Q$,来显示求解$P$矩阵。

• 生根期(1940-1970)

  将李亚普诺夫LMI问题应用在实际的应用中；

  提出了应用图形方法求解LMI；

• 成长期(1970-2000)

  正实引理 —— 将很多问题转化为LMI形式

  凸优化算法应用 —— 为LMI求解提供了成熟的求解工具

• 繁荣期(2000-现在)

  在鲁棒控制等领域应用很广；

参考文献

[1] Duan, G.-R., & Yu, H.-H. (2013). LMIs in Control Systems: Analysis, Design and Applications (1st ed.). CRC Press. https://doi.org/10.1201/b15060, PDF：library.lol/main/1D9AAC1BED0618920BBED953215695E2 学习视频：https://www.bilibili.com/video/BV1jt411U7xj?p=1

[2] K.-Z. Liu and Y. Yao, Robust Control: Theory and Applications. Hoboken, NJ, USA: Wiley, 2016.

[3] 刘金琨. 基于 LMI 的控制系统设计, 分析及 MATLAB 仿真[M]. 清华大学出版社, 2020.文章来源地址https://www.toymoban.com/news/detail-807334.html

1BED0618920BBED953215695E2](http://library.lol/main/1D9AAC1BED0618920BBED953215695E2) 学习视频：https://www.bilibili.com/video/BV1jt411U7xj?p=1

[2] K.-Z. Liu and Y. Yao, Robust Control: Theory and Applications. Hoboken, NJ, USA: Wiley, 2016.

[3] 刘金琨. 基于 LMI 的控制系统设计, 分析及 MATLAB 仿真[M]. 清华大学出版社, 2020.

到了这里，关于线性矩阵不等式（LMI）（一）：简单介绍的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！