递归和迭代实现二叉树先序、中序、后序和层序遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了递归和迭代实现二叉树先序、中序、后序和层序遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

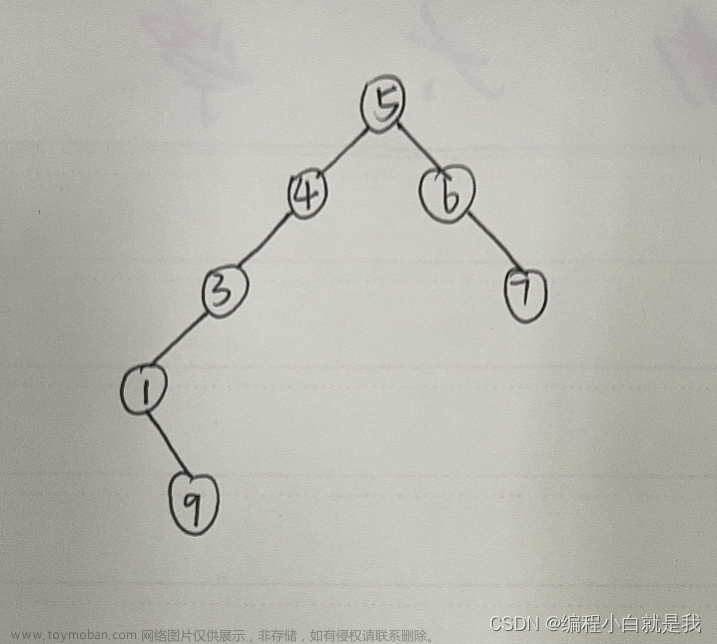
一、递归方法

递归比较简单，直接上代码：

###　1.1 先序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> res = new ArrayList<Integer>();
    public List<Integer> preorderTraversal(TreeNode root) { 
        if(root == null){
            return res;
        }
        //将树节点的值保存在 List 中 便于后续输出
        res.add(root.val);
        preorderTraversal(root.left);
        preorderTraversal(root.right);
        return res;
    }
}

1.2 中序遍历

class Solution {
    List<Integer> res = new ArrayList<Integer>();
    public List<Integer> inorderTraversal(TreeNode root) { 
        if(root == null){
            return res;
        }
        inorderTraversal(root.left);
        res.add(root.val);
        inorderTraversal(root.right);
        return res;
}

1.3 后序遍历

class Solution {
    List<Integer> res = new ArrayList<Integer>();
    public List<Integer> postorderTraversal(TreeNode root) { 
        if(root == null){
            return res;
        }
        postorderTraversal(root.left);
        postorderTraversal(root.right);
        res.add(root.val);
        return res;
}

二、迭代方法

能够用递归方法解决的问题基本都能用非递归方法实现。因为递归方法无非是利用函数栈来保存信息，可以寻找相应的数据结构替代函数栈，同样可以实现相同的功能。下面用栈，类比递归方法来统一实现三种遍历方式：

2.1 先序遍历

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
    	Stack<TreeNode> nodeStack = new Stack<TreeNode>();
    	TreeNode node = root;
        while(node != null || !nodeStack.isEmpty()) { //当指针节点为空，遍历完所有节点时跳出循环
            if(node != null) { //依此遍历当前树最左边的节点。根据递归方法，挨个加入输出 list 中
               res.add(node.val);
               nodeStack.push(node);
               node = node.left;
            }else { //遍历完再看右子树
               node = nodeStack.pop();
               node = node.right;
            }
        }
        return res;
    }
}

2.2 中序遍历

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
    	Stack<TreeNode> nodeStack = new Stack<TreeNode>();
    	TreeNode node = root;
        while(node != null || !nodeStack.isEmpty()) { //当指针节点为空，遍历完所有节点时跳出循环
            if(node != null) { //依此遍历当前树最左边的节点
               nodeStack.push(node);
               node = node.left;
            }else { //遍历完左子树最左节点后，根据递归方法，挨个加入进输出 list 中再看右子树
               node = nodeStack.pop();
               res.add(node.val);
               node = node.right;
            }
        }
        return res;
    }
}

2.3 后序遍历

其实后序遍历，可以利用前序遍历中先遍历右子树，形成 根->右子树->左子树 和后序完全相反的顺序，然后再将该顺序逆序，最后得到后序遍历的顺序。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
        Stack<TreeNode> nodeStack = new Stack<TreeNode>();
        Stack<TreeNode> rStack = new Stack<TreeNode>(); //用一个栈来进行最后 List 反转
        TreeNode node = root;
        while(node != null || !nodeStack.isEmpty()) { //当指针节点为空，遍历完所有节点时跳出循环
            if(node != null) { //依此遍历当前树最右边的节点
               rStack.push(node);
               nodeStack.push(node);
               node = node.right;
            }else { //遍历完右子树最右节点
               node = nodeStack.pop();
               node = node.left;
            }
        }
        while(!rStack.isEmpty()){
            res.add(rStack.pop().val);
        }
        return res;
    }
}

2.4 层序遍历

利用队列来实现层序遍历

基本思想是：

入队就出队，并判断是否有子节点，使用当前队列中的元素作为限制条件
- 有则入队，没有下一步
当所有子节点为空，且全部节点出队后循环结束，输出队列

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        //设置返回数组和队列
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        Queue<TreeNode> Q = new LinkedList<TreeNode>();
        if(root == null) {
            return res;
        }
        Q.offer(root);
        //判断条件
        while(!Q.isEmpty()) {
            int size = Q.size();
            List<Integer> list = new ArrayList<Integer>();
            for(int i = 1; i <= size; i++) {
                TreeNode pnode = Q.poll();
                list.add(pnode.val);
                if(pnode.left != null) {
                    Q.offer(pnode.left);
                }
                if(pnode.right != null){
                    Q.offer(pnode.right);
                }
            }
            res.add(list);
        }
        return res;
    }
}