数据结构（五）数据结构与算法中的经典题-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构（五）数据结构与算法中的经典题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文是在原本数据结构与算法闯关的基础上总结得来，加入了自己的理解和部分习题讲解。至此数据结构介绍已完结，后续会把数据结构算法题系列更完。
原活动链接

邀请码: JL57F5

闯关题：有关于数据结构与算法中的经典题

根据要求完成题目
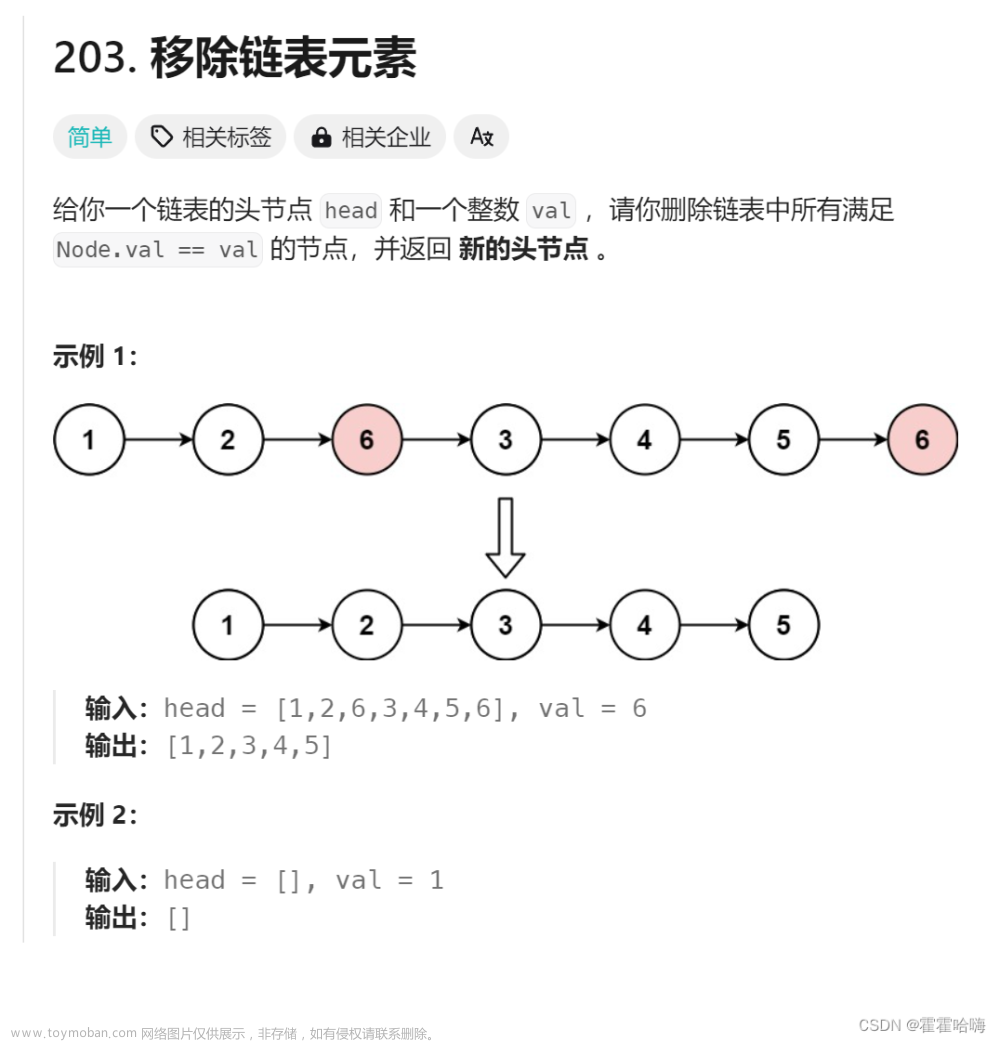
Q1. (单选）以下哪些数据结构支持随机访问？
A. 数组
B. 单链表
C. 双向链表
D. 队列
E. 栈

Q2. (单选）下列哪个操作与队列的机制无关？
A. 入队
B. 出队
C. 获取队首元素
D. 更改队尾元素

Q3. (单选）以下哪种数据结构可以用于实现浏览器的前进和后退功能？
A. 栈
B. 队列
C. 数组
D. 堆
E. 哈希表

class Browser:
def init(self):
self.back_stack = [] # 后退栈
self.forward_stack = [] # 前进栈
self.current_page = None # 当前页面

def visit_page(self, page):
    if self.current_page is not None:
        self.back_stack.append(self.current_page)
    self.current_page = page
    self.forward_stack = []

def go_back(self):
    if len(self.back_stack) > 0:
        self.forward_stack.append(self.current_page)
        self.current_page = self.back_stack.pop()

def go_forward(self):
    if len(self.forward_stack) > 0:
        self.back_stack.append(self.current_page)
        self.current_page = self.forward_stack.pop()mm

在上述示例中，Browser类使用back_stack和forward_stack两个栈来实现浏览器的前进和后退功能。visit_page方法用于访问新页面，将当前页面推入back_stack，并清空forward_stack。go_back方法从back_stack中弹出最近访问的页面，并将其推入forward_stack。go_forward方法从forward_stack中弹出最近访问的页面，并将其推入back_stack。

通过使用栈数据结构，可以轻松实现浏览器的前进和后退功能，并保持页面访问的顺序。

Q4. (单选）哈希表可以借助哪种数据结构来实现？
A. 图
B. 链表
C. 二叉树
D. 堆

Q5. (单选）以下哪种操作不是哈希表的基本操作？
A. 插入（Insert）
B. 删除（Delete）
C. 修改（Update）
D. 查找（Search）
E. 排序（Sort）

背景：
假设你是一家餐厅的后厨管理员，你需要负责安排顾客的点餐和餐厅后勤工作。由于餐厅人流量比较大，顾客数量众多，为了保证餐厅运营效率以及顾客满意度，你需要实现一种基于队列的排队算法。

问题：
实现一个基于队列的顾客排队模块。

方案：
我们可以使用队列来实现顾客排队。每个顾客到餐厅后，需要先进行排队，等待服务员叫号后进入餐厅就餐。我们可以将每个顾客看做一个个元素，先到先服务，每次将队前元素出队即可。同时，在顾客进入餐厅之前，我们还可以预估每个顾客的点餐时间，将顾客插入到队列中之后，根据队列中前后的顺序以及每个顾客的点餐时间，实现一种优先级算法，让点餐时间短的顾客先被叫号。

class Restaurant:
    def __init__(self):
        self.queue = []  # 初始化餐厅的队列为空列表

    def add_customer_to_queue(self, customer, order_time):
        """
        将顾客加入队列中。
        Args:
          customer (str): 顾客名字。
          order_time (float): 顾客点餐时间。
        """
        if len(self.queue) == 0:  # 如果队列为空
            self.queue.append((customer, order_time)) # 题目q6 : 直接将顾客名字和点餐时间作为元组加入队列
        else:
            for i in range(len(self.queue)):  # 遍历队列中的顾客
                if order_time < self.queue[i][1]:  # 如果当前顾客的点餐时间比要插入的顾客点餐时间大
                    self.queue.insert(i, (customer, order_time))  # 将顾客插入到当前顾客之前的位置
                    break  # 插入完成后中断循环
            else:
                self.queue.append((customer, order_time))  # 如果没有找到合适的位置，则将顾客添加到队列末尾

    def call_customer(self):
        """
        叫号，将队首的顾客出队列。
        Returns:
          顾客名字。
        """
        if len(self.queue) == 0: # 题目q7 :  如果队列为空
            return None  # 返回None表示没有顾客等待
        else:
            customer = self.queue.pop(0)[0]  # 弹出队首顾客并获取其名字
            return customer  # 返回顾客名字作为结果

在上面的代码中，我们定义了一个Restaurant类，类中包含了一个queue列表，用于存放排队中的顾客。类中定义了add_customer_to_queue方法，将顾客加入队列中；call_customer方法用于叫号，将队首的顾客出队列。

可以使用下面的代码来测试上面的餐厅排队模块的正确性：

# 创建一个餐厅实例
r = Restaurant()

# 添加顾客到队列中
r.add_customer_to_queue("Alice", 2)
r.add_customer_to_queue("Bob", 3)
r.add_customer_to_queue("Cathy", 1)

# 叫号
print(r.call_customer())  # Cathy
print(r.call_customer())  # Alice
print(r.call_customer())  # Bob
print(r.call_customer())  # None

Cathy
Alice
Bob
None

在上面的测试代码中，我们创建一个餐厅实例，向餐厅排队模块添加几个顾客，然后调用call_customer方法叫号，检查叫号时的顾客排队顺序是否满足点餐时间的先后关系。
实现我们要求的模块功能已经正确实现，并可以按照点餐时间的先后顺序将顾客进行排队。

观察上面的实现代码，完成下面的单选题（注意仔细查看注释和前后代码）

Q6. 代码第13行为空，现在需要实现 直接将顾客名字和点餐时间作为元组加入队列，下面哪个选项为正确代码，选择正确选项并把结果赋值给a6

A : self.queue.append((add_customer_to_queue, order_time))

B : self.queue.append((customer, order_time))

C : self.queue.insert((add_customer_to_queue, order_time))

D : self.queue.insert((customer, order_time))

Q7. 代码第28行为空，现在需要实现 如果队列为空的代码，下面哪个选项为正确代码，选择正确选项并把结果赋值给a7

A : if count(self.queue) == 0:

B : if len(self.queue) == 0:

C : if len(self.queue) is None:

D : if count(self.queue) is None:

#填入你的答案
a1 = 'A'  # 如 a1 = 'A'
a2 = 'D'  # 如 a2 = 'A'
a3 = 'A'  # 如 a3 = 'A'  
a4 = 'B'  # 如 a4 = 'A'  
a5 = 'E'  # 如 a5 = 'A'  
a6 = 'B'  # 如 a6 = 'A'
a7 = 'B'  # 如 a7 = 'A'

将结果保存为 csv 文件
csv 需要有两列，列名：id、answer。其中，id 列为题号，如 q1、q2；answer 列为 STEP1 中各题你计算出来的结果。💡 这一步的代码你无需修改，直接运行即可。文章来源地址https://www.toymoban.com/news/detail-807812.html

# 生成 csv 作业答案文件
def save_csv(a1, a2, a3, a4, a5,a6,a7) : 
    import pandas as pd
    df = pd.DataFrame({"id": ["q1", "q2", "q3", "q4","q5","q6","q7"], "answer": [a1, a2, a3,a4,a5,a6,a7]})
    df.to_csv("answer_ago_1_5.csv", index=None)

save_csv(a1, a2, a3, a4, a5,a6,a7)  # 运行这个cell,生成答案文件；该文件在左侧文件树project工作区下，你可以自行右击下载或者读取查看