深度优先搜索（DFS、深搜）和广度优先搜索（BFS、广搜）

目录

深度优先搜索（DFS、深搜）和广度优先搜索（BFS、广搜）

深度优先搜索（简称“深搜”或DFS）

广度优先搜索

总结

深度优先生成树和广度优先生成树

非连通图的生成森林

深度优先生成森林

广度优先生成森林

深度优先搜索（DFS、深搜）和广度优先搜索（BFS、广搜）

深度优先搜索（简称“深搜”或DFS）

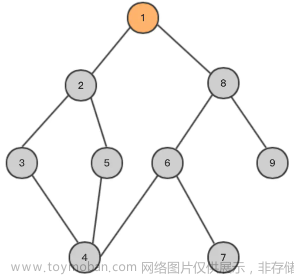
图 1 无向图

深度优先搜索的过程类似于树的先序遍历，首先从例子中体会深度优先搜索。例如图 1 是一个无向图，采用深度优先算法遍历这个图的过程为：

1. 首先任意找一个未被遍历过的顶点，例如从 V1 开始，由于 V1 率先访问过了，所以，需要标记 V1 的状态为访问过；
2. 然后遍历 V1 的邻接点，例如访问 V2 ，并做标记，然后访问 V2 的邻接点，例如 V4 （做标记），然后 V8 ，然后 V5 ；
3. 当继续遍历 V5 的邻接点时，根据之前做的标记显示，所有邻接点都被访问过了。此时，从 V5 回退到 V8 ，看 V8 是否有未被访问过的邻接点，如果没有，继续回退到 V4 ， V2 ， V1 ；
4. 通过查看 V1 ，找到一个未被访问过的顶点 V3 ，继续遍历，然后访问 V3  邻接点 V6 ，然后 V7 ；
5. 由于 V7 没有未被访问的邻接点，所有回退到 V6 ，继续回退至 V3 ，最后到达 V1 ，发现没有未被访问的；
6. 最后一步需要判断是否所有顶点都被访问，如果还有没被访问的，以未被访问的顶点为第一个顶点，继续依照上边的方式进行遍历。

根据上边的过程，可以得到图 1 通过深度优先搜索获得的顶点的遍历次序为：

V1 -> V2 -> V4 -> V8 -> V5 -> V3 -> V6 -> V7

所谓深度优先搜索，是从图中的一个顶点出发，每次遍历当前访问顶点的临界点，一直到访问的顶点没有未被访问过的临界点为止。然后采用依次回退的方式，查看来的路上每一个顶点是否有其它未被访问的临界点。访问完成后，判断图中的顶点是否已经全部遍历完成，如果没有，以未访问的顶点为起始点，重复上述过程。

深度优先搜索是一个不断回溯的过程。

采用深度优先搜索算法遍历图的实现代码为：

1. #include <stdio.h>
3. #define MAX_VERtEX_NUM 20 //顶点的最大个数
4. #define VRType int //表示顶点之间的关系的变量类型
5. #define InfoType char //存储弧或者边额外信息的指针变量类型
6. #define VertexType int //图中顶点的数据类型
8. typedef enum{false,true}bool; //定义bool型常量
9. bool visited[MAX_VERtEX_NUM]; //设置全局数组，记录标记顶点是否被访问过
11. typedef struct {
12. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
13. InfoType * info; //弧或边额外含有的信息指针
14. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
16. typedef struct {
17. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
18. AdjMatrix arcs; //二维数组，记录顶点之间的关系
19. int vexnum,arcnum; //记录图的顶点数和弧（边）数
20. }MGraph;
21. //根据顶点本身数据，判断出顶点在二维数组中的位置
22. int LocateVex(MGraph * G,VertexType v){
23. int i=0;
24. //遍历一维数组，找到变量v
25. for (; i<G->vexnum; i++) {
26. if (G->vexs[i]==v) {
27. break;
28. }
29. }
30. //如果找不到，输出提示语句，返回-1
31. if (i>G->vexnum) {
32. printf("no such vertex.\n");
33. return -1;
34. }
35. return i;
36. }
37. //构造无向图
38. void CreateDN(MGraph *G){
39. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
40. for (int i=0; i<G->vexnum; i++) {
41. scanf("%d",&(G->vexs[i]));
42. }
43. for (int i=0; i<G->vexnum; i++) {
44. for (int j=0; j<G->vexnum; j++) {
45. G->arcs[i][j].adj=0;
46. G->arcs[i][j].info=NULL;
47. }
48. }
49. for (int i=0; i<G->arcnum; i++) {
50. int v1,v2;
51. scanf("%d,%d",&v1,&v2);
52. int n=LocateVex(G, v1);
53. int m=LocateVex(G, v2);
54. if (m==-1 ||n==-1) {
55. printf("no this vertex\n");
56. return;
57. }
58. G->arcs[n][m].adj=1;
59. G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
60. }
61. }
63. int FirstAdjVex(MGraph G,int v)
64. {
65. //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
66. for(int i = 0; i<G.vexnum; i++){
67. if( G.arcs[v][i].adj ){
68. return i;
69. }
70. }
71. return -1;
72. }
73. int NextAdjVex(MGraph G,int v,int w)
74. {
75. //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
76. for(int i = w+1; i<G.vexnum; i++){
77. if(G.arcs[v][i].adj){
78. return i;
79. }
80. }
81. return -1;
82. }
83. void visitVex(MGraph G, int v){
84. printf("%d ",G.vexs[v]);
85. }
86. void DFS(MGraph G,int v){
87. visited[v] = true;//标记为true
88. visitVex( G, v); //访问第v 个顶点
89. //从该顶点的第一个边开始，一直到最后一个边，对处于边另一端的顶点调用DFS函数
90. for(int w = FirstAdjVex(G,v); w>=0; w = NextAdjVex(G,v,w)){
91. //如果该顶点的标记位false，证明未被访问，调用深度优先搜索函数
92. if(!visited[w]){
93. DFS(G,w);
94. }
95. }
96. }
97. //深度优先搜索
98. void DFSTraverse(MGraph G){//
99. int v;
100. //将用做标记的visit数组初始化为false
101. for( v = 0; v < G.vexnum; ++v){
102. visited[v] = false;
103. }
104. //对于每个标记为false的顶点调用深度优先搜索函数
105. for( v = 0; v < G.vexnum; v++){
106. //如果该顶点的标记位为false，则调用深度优先搜索函数
107. if(!visited[v]){
108. DFS( G, v);
109. }
110. }
111. }
113. int main() {
114. MGraph G;//建立一个图的变量
115. CreateDN(&G);//初始化图
116. DFSTraverse(G);//深度优先搜索图
117. return 0;
118. }

以图 1 为例，运行结果为：

8,9
1
2
3
4
5
6
7
8
1,2
2,4
2,5
4,8
5,8
1,3
3,6
6,7
7,3
1 2 4 8 5 3 6 7

广度优先搜索

广度优先搜索类似于树的层次遍历。从图中的某一顶点出发，遍历每一个顶点时，依次遍历其所有的邻接点，然后再从这些邻接点出发，同样依次访问它们的邻接点。按照此过程，直到图中所有被访问过的顶点的邻接点都被访问到。

最后还需要做的操作就是查看图中是否存在尚未被访问的顶点，若有，则以该顶点为起始点，重复上述遍历的过程。

还拿图 1 中的无向图为例，假设 V1 作为起始点，遍历其所有的邻接点 V2 和 V3 ，以 V2 为起始点，访问邻接点 V4 和 V5 ，以 V3 为起始点，访问邻接点 V6 、 V7 ，以 V4 为起始点访问 V8 ，以 V5 为起始点，由于 V5 所有的起始点已经全部被访问，所有直接略过， V6 和 V7 也是如此。
以 V1 为起始点的遍历过程结束后，判断图中是否还有未被访问的点，由于图 1 中没有了，所以整个图遍历结束。遍历顶点的顺序为：

V1 -> V2 -> v3 -> V4 -> V5 -> V6 -> V7 -> V8

广度优先搜索的实现需要借助队列这一特殊数据结构，实现代码为：

1. #include <stdio.h>
2. #include <stdlib.h>
3. #define MAX_VERtEX_NUM 20 //顶点的最大个数
4. #define VRType int //表示顶点之间的关系的变量类型
5. #define InfoType char //存储弧或者边额外信息的指针变量类型
6. #define VertexType int //图中顶点的数据类型
7. typedef enum{false,true}bool; //定义bool型常量
8. bool visited[MAX_VERtEX_NUM]; //设置全局数组，记录标记顶点是否被访问过
9. typedef struct Queue{
10. VertexType data;
11. struct Queue * next;
12. }Queue;
13. typedef struct {
14. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
15. InfoType * info; //弧或边额外含有的信息指针
16. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
18. typedef struct {
19. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
20. AdjMatrix arcs; //二维数组，记录顶点之间的关系
21. int vexnum,arcnum; //记录图的顶点数和弧（边）数
22. }MGraph;
23. //根据顶点本身数据，判断出顶点在二维数组中的位置
24. int LocateVex(MGraph * G,VertexType v){
25. int i=0;
26. //遍历一维数组，找到变量v
27. for (; i<G->vexnum; i++) {
28. if (G->vexs[i]==v) {
29. break;
30. }
31. }
32. //如果找不到，输出提示语句，返回-1
33. if (i>G->vexnum) {
34. printf("no such vertex.\n");
35. return -1;
36. }
37. return i;
38. }
39. //构造无向图
40. void CreateDN(MGraph *G){
41. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
42. for (int i=0; i<G->vexnum; i++) {
43. scanf("%d",&(G->vexs[i]));
44. }
45. for (int i=0; i<G->vexnum; i++) {
46. for (int j=0; j<G->vexnum; j++) {
47. G->arcs[i][j].adj=0;
48. G->arcs[i][j].info=NULL;
49. }
50. }
51. for (int i=0; i<G->arcnum; i++) {
52. int v1,v2;
53. scanf("%d,%d",&v1,&v2);
54. int n=LocateVex(G, v1);
55. int m=LocateVex(G, v2);
56. if (m==-1 ||n==-1) {
57. printf("no this vertex\n");
58. return;
59. }
60. G->arcs[n][m].adj=1;
61. G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
62. }
63. }
65. int FirstAdjVex(MGraph G,int v)
66. {
67. //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
68. for(int i = 0; i<G.vexnum; i++){
69. if( G.arcs[v][i].adj ){
70. return i;
71. }
72. }
73. return -1;
74. }
75. int NextAdjVex(MGraph G,int v,int w)
76. {
77. //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
78. for(int i = w+1; i<G.vexnum; i++){
79. if(G.arcs[v][i].adj){
80. return i;
81. }
82. }
83. return -1;
84. }
85. //操作顶点的函数
86. void visitVex(MGraph G, int v){
87. printf("%d ",G.vexs[v]);
88. }
89. //初始化队列
90. void InitQueue(Queue ** Q){
91. (*Q)=(Queue*)malloc(sizeof(Queue));
92. (*Q)->next=NULL;
93. }
94. //顶点元素v进队列
95. void EnQueue(Queue **Q,VertexType v){
96. Queue * element=(Queue*)malloc(sizeof(Queue));
97. element->data=v;
98. element->next = NULL;
99. Queue * temp=(*Q);
100. while (temp->next!=NULL) {
101. temp=temp->next;
102. }
103. temp->next=element;
104. }
105. //队头元素出队列
106. void DeQueue(Queue **Q,int *u){
107. (*u)=(*Q)->next->data;
108. (*Q)->next=(*Q)->next->next;
109. }
110. //判断队列是否为空
111. bool QueueEmpty(Queue *Q){
112. if (Q->next==NULL) {
113. return true;
114. }
115. return false;
116. }
117. //广度优先搜索
118. void BFSTraverse(MGraph G){//
119. int v;
120. //将用做标记的visit数组初始化为false
121. for( v = 0; v < G.vexnum; ++v){
122. visited[v] = false;
123. }
124. //对于每个标记为false的顶点调用深度优先搜索函数
125. Queue * Q;
126. InitQueue(&Q);
127. for( v = 0; v < G.vexnum; v++){
128. if(!visited[v]){
129. visited[v]=true;
130. visitVex(G, v);
131. EnQueue(&Q, G.vexs[v]);
132. while (!QueueEmpty(Q)) {
133. int u;
134. DeQueue(&Q, &u);
135. u=LocateVex(&G, u);
136. for (int w=FirstAdjVex(G, u); w>=0; w=NextAdjVex(G, u, w)) {
137. if (!visited[w]) {
138. visited[w]=true;
139. visitVex(G, w);
140. EnQueue(&Q, G.vexs[w]);
141. }
142. }
143. }
144. }
145. }
146. }
147. int main() {
148. MGraph G;//建立一个图的变量
149. CreateDN(&G);//初始化图
150. BFSTraverse(G);//广度优先搜索图
151. return 0;
152. }

例如，使用上述程序代码遍历图 1 中的无向图，运行结果为：

8,9
1
2
3
4
5
6
7
8
1,2
2,4
2,5
4,8
5,8
1,3
3,6
6,7
7,3
1 2 3 4 5 6 7 8

总结

本节介绍了两种遍历图的方式：深度优先搜索算法和广度优先搜索算法。深度优先搜索算法的实现运用的主要是回溯法，类似于树的先序遍历算法。广度优先搜索算法借助队列的先进先出的特点，类似于树的层次遍历。

深度优先生成树和广度优先生成树

其实在对无向图进行遍历的时候，遍历过程中所经历过的图中的顶点和边的组合，就是图的生成树或者生成森林。

图 1 无向图
 12485367

例如，图 1 中的无向图是由 V1～V7 的顶点和编号分别为 a～i 的边组成。当使用深度优先搜索算法时，假设 V1 作为遍历的起始点，涉及到的顶点和边的遍历顺序为（不唯一）：

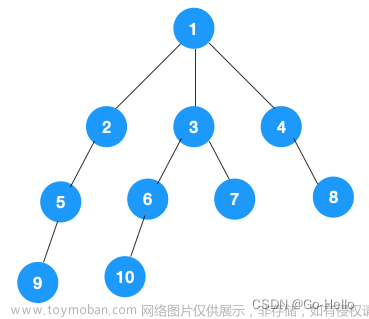
此种遍历顺序构建的生成树为：

 12485367
图 2 深度优先生成树

由深度优先搜索得到的树为深度优先生成树。同理，广度优先搜索生成的树为广度优先生成树，图 1 无向图以顶点 V1 为起始点进行广度优先搜索遍历得到的树，如图 3 所示：

图 3 广度优先生成树

非连通图的生成森林

非连通图在进行遍历时，实则是对非连通图中每个连通分量分别进行遍历，在遍历过程经过的每个顶点和边，就构成了每个连通分量的生成树。

非连通图中，多个连通分量构成的多个生成树为非连通图的生成森林。

深度优先生成森林

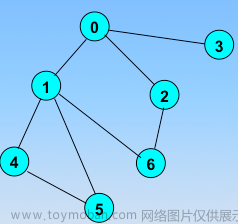
选择小的数字作为开头；

图 4 深度优先生成森林

例如，对图 4 中的非连通图 （a） 采用深度优先搜索算法遍历时，得到的深度优先生成森林（由 3 个深度优先生成树构成）如 （b） 所示（不唯一）。

非连通图在遍历生成森林时，可以采用孩子兄弟表示法将森林转化为一整棵二叉树进行存储。

具体实现的代码：

1. #include <stdio.h>
2. #include <stdlib.h>
3. #define MAX_VERtEX_NUM 20 //顶点的最大个数
4. #define VRType int //表示顶点之间的关系的变量类型
5. #define VertexType int //图中顶点的数据类型
6. typedef enum{false,true}bool; //定义bool型常量
7. bool visited[MAX_VERtEX_NUM]; //设置全局数组，记录标记顶点是否被访问过
9. typedef struct {
10. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
11. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
13. typedef struct {
14. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
15. AdjMatrix arcs; //二维数组，记录顶点之间的关系
16. int vexnum,arcnum; //记录图的顶点数和弧（边）数
17. }MGraph;
18. //孩子兄弟表示法的链表结点结构
19. typedef struct CSNode{
20. VertexType data;
21. struct CSNode * lchild;//孩子结点
22. struct CSNode * nextsibling;//兄弟结点
23. }*CSTree,CSNode;
24. //根据顶点本身数据，判断出顶点在二维数组中的位置
25. int LocateVex(MGraph G,VertexType v){
26. int i=0;
27. //遍历一维数组，找到变量v
28. for (; i<G.vexnum; i++) {
29. if (G.vexs[i]==v) {
30. break;
31. }
32. }
33. //如果找不到，输出提示语句，返回-1
34. if (i>G.vexnum) {
35. printf("no such vertex.\n");
36. return -1;
37. }
38. return i;
39. }
40. //构造无向图
41. void CreateDN(MGraph *G){
42. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
43. getchar();
44. for (int i=0; i<G->vexnum; i++) {
45. scanf("%d",&(G->vexs[i]));
46. }
47. for (int i=0; i<G->vexnum; i++) {
48. for (int j=0; j<G->vexnum; j++) {
49. G->arcs[i][j].adj=0;
50. }
51. }
52. for (int i=0; i<G->arcnum; i++) {
53. int v1,v2;
54. scanf("%d,%d",&v1,&v2);
55. int n=LocateVex(*G, v1);
56. int m=LocateVex(*G, v2);
57. if (m==-1 ||n==-1) {
58. printf("no this vertex\n");
59. return;
60. }
61. G->arcs[n][m].adj=1;
62. G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
63. }
64. }
65. int FirstAdjVex(MGraph G,int v)
66. {
67. //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
68. for(int i = 0; i<G.vexnum; i++){
69. if( G.arcs[v][i].adj ){
70. return i;
71. }
72. }
73. return -1;
74. }
75. int NextAdjVex(MGraph G,int v,int w)
76. {
77. //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
78. for(int i = w+1; i<G.vexnum; i++){
79. if(G.arcs[v][i].adj){
80. return i;
81. }
82. }
83. return -1;
84. }
85. void DFSTree(MGraph G,int v,CSTree*T){
86. //将正在访问的该顶点的标志位设为true
87. visited[v]=true;
88. bool first=true;
89. CSTree q=NULL;
90. //依次遍历该顶点的所有邻接点
91. for (int w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G, v, w)) {
92. //如果该临界点标志位为false，说明还未访问
93. if (!visited[w]) {
94. //为该邻接点初始化为结点
95. CSTree p=(CSTree)malloc(sizeof(CSNode));
96. p->data=G.vexs[w];
97. p->lchild=NULL;
98. p->nextsibling=NULL;
99. //该结点的第一个邻接点作为孩子结点，其它邻接点作为孩子结点的兄弟结点
100. if (first) {
101. (*T)->lchild=p;
102. first=false;
103. }
104. //否则，为兄弟结点
105. else{
106. q->nextsibling=p;
107. }
108. q=p;
109. //以当前访问的顶点为树根，继续访问其邻接点
110. DFSTree(G, w, &q);
111. }
112. }
113. }
114. //深度优先搜索生成森林并转化为二叉树
115. void DFSForest(MGraph G,CSTree *T){
116. (*T)=NULL;
117. //每个顶点的标记为初始化为false
118. for (int v=0; v<G.vexnum; v++) {
119. visited[v]=false;
120. }
121. CSTree q=NULL;
122. //遍历每个顶点作为初始点，建立深度优先生成树
123. for (int v=0; v<G.vexnum; v++) {
124. //如果该顶点的标记位为false，证明未访问过
125. if (!(visited[v])) {
126. //新建一个结点，表示该顶点
127. CSTree p=(CSTree)malloc(sizeof(CSNode));
128. p->data=G.vexs[v];
129. p->lchild=NULL;
130. p->nextsibling=NULL;
131. //如果树未空，则该顶点作为树的树根
132. if (!(*T)) {
133. (*T)=p;
135. }
136. //该顶点作为树根的兄弟结点
137. else{
138. q->nextsibling=p;
139. }
140. //每次都要把q指针指向新的结点，为下次添加结点做铺垫
141. q=p;
142. //以该结点为起始点，构建深度优先生成树
143. DFSTree(G,v,&p);
144. }
145. }
146. }
147. //前序遍历二叉树
148. void PreOrderTraverse(CSTree T){
149. if (T) {
150. printf("%d ",T->data);
151. PreOrderTraverse(T->lchild);
152. PreOrderTraverse(T->nextsibling);
153. }
154. return;
155. }
156. int main() {
157. MGraph G;//建立一个图的变量
158. CreateDN(&G);//初始化图
159. CSTree T;
160. DFSForest(G, &T);
161. PreOrderTraverse(T);
162. return 0;
163. }

运行程序，拿图 4（a）中的非连通图为例，构建的深度优先生成森林，使用孩子兄弟表示法表示为：

图5 孩子兄弟表示法表示深度优先生成森林

图中，3 种颜色的树各代表一棵深度优先生成树，使用孩子兄弟表示法表示，也就是将三棵树的树根相连，第一棵树的树根作为整棵树的树根。

运行结果

13,13
1
2
3
4
5
6
7
8
9
10
11
12
13
1,2
1,3
1,6
1,12
2,13
4,5
7,8
7,10
7,9
8,10
11,12
11,13
12,13
1 2 13 11 12 3 6 4 5 7 8 10 9

广度优先生成森林

非连通图采用广度优先搜索算法进行遍历时，经过的顶点以及边的集合为该图的广度优先生成森林。

拿图 4（a）中的非连通图为例，通过广度优先搜索得到的广度优先生成森林用孩子兄弟表示法为：

图6 广度优先生成森林（孩子兄弟表示法）

实现代码为：

1. #include <stdio.h>
2. #include <stdlib.h>
3. #define MAX_VERtEX_NUM 20 //顶点的最大个数
4. #define VRType int //表示顶点之间的关系的变量类型
5. #define InfoType char //存储弧或者边额外信息的指针变量类型
6. #define VertexType int //图中顶点的数据类型
7. typedef enum{false,true}bool; //定义bool型常量
8. bool visited[MAX_VERtEX_NUM]; //设置全局数组，记录标记顶点是否被访问过
9. typedef struct {
10. VRType adj; //对于无权图，用 1 或 0 表示是否相邻；对于带权图，直接为权值。
11. InfoType * info; //弧或边额外含有的信息指针
12. }ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
14. typedef struct {
15. VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
16. AdjMatrix arcs; //二维数组，记录顶点之间的关系
17. int vexnum,arcnum; //记录图的顶点数和弧（边）数
18. }MGraph;
20. typedef struct CSNode{
21. VertexType data;
22. struct CSNode * lchild;//孩子结点
23. struct CSNode * nextsibling;//兄弟结点
24. }*CSTree,CSNode;
26. typedef struct Queue{
27. CSTree data;//队列中存放的为树结点
28. struct Queue * next;
29. }Queue;
31. //根据顶点本身数据，判断出顶点在二维数组中的位置
32. int LocateVex(MGraph * G,VertexType v){
33. int i=0;
34. //遍历一维数组，找到变量v
35. for (; i<G->vexnum; i++) {
36. if (G->vexs[i]==v) {
37. break;
38. }
39. }
40. //如果找不到，输出提示语句，返回-1
41. if (i>G->vexnum) {
42. printf("no such vertex.\n");
43. return -1;
44. }
45. return i;
46. }
47. //构造无向图
48. void CreateDN(MGraph *G){
49. scanf("%d,%d",&(G->vexnum),&(G->arcnum));
50. for (int i=0; i<G->vexnum; i++) {
51. scanf("%d",&(G->vexs[i]));
52. }
53. for (int i=0; i<G->vexnum; i++) {
54. for (int j=0; j<G->vexnum; j++) {
55. G->arcs[i][j].adj=0;
56. G->arcs[i][j].info=NULL;
57. }
58. }
59. for (int i=0; i<G->arcnum; i++) {
60. int v1,v2;
61. scanf("%d,%d",&v1,&v2);
62. int n=LocateVex(G, v1);
63. int m=LocateVex(G, v2);
64. if (m==-1 ||n==-1) {
65. printf("no this vertex\n");
66. return;
67. }
68. G->arcs[n][m].adj=1;
69. G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
70. }
71. }
73. int FirstAdjVex(MGraph G,int v)
74. {
75. //查找与数组下标为v的顶点之间有边的顶点，返回它在数组中的下标
76. for(int i = 0; i<G.vexnum; i++){
77. if( G.arcs[v][i].adj ){
78. return i;
79. }
80. }
81. return -1;
82. }
83. int NextAdjVex(MGraph G,int v,int w)
84. {
85. //从前一个访问位置w的下一个位置开始，查找之间有边的顶点
86. for(int i = w+1; i<G.vexnum; i++){
87. if(G.arcs[v][i].adj){
88. return i;
89. }
90. }
91. return -1;
92. }
94. //初始化队列
95. void InitQueue(Queue ** Q){
96. (*Q)=(Queue*)malloc(sizeof(Queue));
97. (*Q)->next=NULL;
98. }
99. //结点v进队列
100. void EnQueue(Queue **Q,CSTree T){
101. Queue * element=(Queue*)malloc(sizeof(Queue));
102. element->data=T;
103. element->next=NULL;
105. Queue * temp=(*Q);
106. while (temp->next!=NULL) {
107. temp=temp->next;
108. }
109. temp->next=element;
110. }
111. //队头元素出队列
112. void DeQueue(Queue **Q,CSTree *u){
113. (*u)=(*Q)->next->data;
114. (*Q)->next=(*Q)->next->next;
115. }
116. //判断队列是否为空
117. bool QueueEmpty(Queue *Q){
118. if (Q->next==NULL) {
119. return true;
120. }
121. return false;
122. }
124. void BFSTree(MGraph G,int v,CSTree*T){
125. CSTree q=NULL;
126. Queue * Q;
127. InitQueue(&Q);
128. //根结点入队
129. EnQueue(&Q, (*T));
130. //当队列为空时，证明遍历完成
131. while (!QueueEmpty(Q)) {
132. bool first=true;
133. //队列首个结点出队
134. DeQueue(&Q,&q);
135. //判断结点中的数据在数组中的具体位置
136. int v=LocateVex(&G,q->data);
137. //已经访问过的更改其标志位
138. visited[v]=true;
139. //遍历以出队结点为起始点的所有邻接点
140. for (int w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v, w)) {
141. //标志位为false，证明未遍历过
142. if (!visited[w]) {
143. //新建一个结点 p，存放当前遍历的顶点
144. CSTree p=(CSTree)malloc(sizeof(CSNode));
145. p->data=G.vexs[w];
146. p->lchild=NULL;
147. p->nextsibling=NULL;
148. //当前结点入队
149. EnQueue(&Q, p);
150. //更改标志位
151. visited[w]=true;
152. //如果是出队顶点的第一个邻接点，设置p结点为其左孩子
153. if (first) {
154. q->lchild=p;
155. first=false;
156. }
157. //否则设置其为兄弟结点
158. else{
159. q->nextsibling=p;
160. }
161. q=p;
162. }
163. }
164. }
165. }
166. //广度优先搜索生成森林并转化为二叉树
167. void BFSForest(MGraph G,CSTree *T){
168. (*T)=NULL;
169. //每个顶点的标记为初始化为false
170. for (int v=0; v<G.vexnum; v++) {
171. visited[v]=false;
172. }
173. CSTree q=NULL;
174. //遍历图中所有的顶点
175. for (int v=0; v<G.vexnum; v++) {
176. //如果该顶点的标记位为false，证明未访问过
177. if (!(visited[v])) {
178. //新建一个结点，表示该顶点
179. CSTree p=(CSTree)malloc(sizeof(CSNode));
180. p->data=G.vexs[v];
181. p->lchild=NULL;
182. p->nextsibling=NULL;
183. //如果树未空，则该顶点作为树的树根
184. if (!(*T)) {
185. (*T)=p;
186. }
187. //该顶点作为树根的兄弟结点
188. else{
189. q->nextsibling=p;
190. }
191. //每次都要把q指针指向新的结点，为下次添加结点做铺垫
192. q=p;
193. //以该结点为起始点，构建广度优先生成树
194. BFSTree(G,v,&p);
195. }
196. }
197. }
198. //前序遍历二叉树
199. void PreOrderTraverse(CSTree T){
200. if (T) {
201. printf("%d ",T->data);
202. PreOrderTraverse(T->lchild);
203. PreOrderTraverse(T->nextsibling);
204. }
205. return;
206. }
207. int main() {
208. MGraph G;//建立一个图的变量
209. CreateDN(&G);//初始化图
210. CSTree T;
211. BFSForest(G, &T);
212. PreOrderTraverse(T);
213. return 0;
214. }

运行结果为：

13,13
1
2
3
4
5
6
7
8
9
10
11
12
13
1,2
1,3
1,6
1,12
2,13
4,5
7,8
7,10
7,9
8,10
11,12
11,13
12,13
1 2 13 3 6 12 11 4 5 7 8 9 10文章来源地址https://www.toymoban.com/news/detail-808216.html

到了这里，关于深度优先搜索（DFS、深搜）和广度优先搜索（BFS、广搜）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！