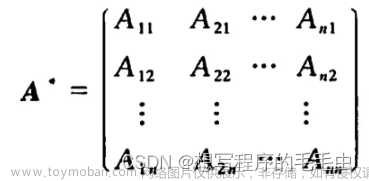
矩阵的三种不变因子
本文主要介绍多项式矩阵的基本概念和等价,用于为相似标准型进行铺垫
一、多项式矩阵
此处将由数组成的矩阵拓展为以多项式为元的矩阵,即多项式矩阵
【定义】多项式矩阵的秩
设 A ( λ ) ∈ F [ λ ] m × n , A ( λ ) ≠ 0 A(\lambda)\in F[\lambda]^{m\times n},A(\lambda)\neq0 A(λ)∈F[λ]m×n,A(λ)=0,如果 A ( λ ) A(\lambda) A(λ) 中存在一个 r ( r ≥ 1 ) r(r\geq1) r(r≥1) 级子式不为0,而所有的 r + 1 r+1 r+1 级子式(如果存在的话)全为0,则称 A ( λ ) A(\lambda) A(λ) 的秩为 r r r,记为 r a n k A ( λ ) = r rank A(\lambda)= r rankA(λ)=r。规定零矩阵的秩为0。
与一般线性代数初等变换的操作类似,最后的到的元只有恒为0才认为其值为0.
【定义】可逆矩阵、逆矩阵
设 A ( λ ) ∈ F [ λ ] n × n A(\lambda)\in F[\lambda]^{n\times n} A(λ)∈F[λ]n×n,如果存在 B ( λ ) ∈ F [ λ ] n × n B(\lambda)\in F[\lambda]^{n\times n} B(λ)∈F[λ]n×n,使得
A ( λ ) B ( λ ) = B ( λ ) A ( λ ) = E A(\lambda)B(\lambda)=B(\lambda)A(\lambda)=E A(λ)B(λ)=B(λ)A(λ)=E
则称 A ( λ ) A(\lambda) A(λ) 为可逆矩阵, B ( λ ) B(\lambda) B(λ)称为 A ( λ ) A(\lambda) A(λ) 的逆矩阵
【定理】可逆的充要条件
设 A ( λ ) ∈ F [ λ ] n × n A(\lambda)\in F[\lambda]^{n\times n} A(λ)∈F[λ]n×n, A ( λ ) A(\lambda) A(λ) 可逆的充要条件是 det ( A ( λ ) ) \det(A(\lambda)) det(A(λ))1是一个非0常数
【定义】非奇异
矩阵满秩的另一个叫法为矩阵非奇异
二、多项式矩阵的等价标准型
【定义】三类初等变换
- 【互换】互换多项式的两行(列)
- 【倍乘】用一个非零常数 c 去乘多项式矩阵的某一行(列)
- 【倍加】将多项式矩阵的某一行(列)的 φ ( λ ) ∈ F [ λ ] \varphi(\lambda)\in F[\lambda] φ(λ)∈F[λ] 倍加到另一行(列)
仅倍加扩展到了乘一个“多项式”,再加到另一行(列)上
- 整数可以整除任何一个多项式,非常好用~
【定理】初等多项式矩阵的性质
- 初等多项式矩阵是可逆矩阵
- 逆矩阵还是同类型的初等多项式矩阵
- 用初等多项式矩阵去左乘(右乘)多项式矩阵 A ( λ ) A(\lambda) A(λ),相当于对 A ( λ ) A(\lambda) A(λ) 进行一次响应的初等行(列)变换
【定义】等价
设 A ( λ ) A(\lambda) A(λ), B ( λ ) ∈ F [ λ ] m × n B(\lambda)\in F[\lambda]^{m\times n} B(λ)∈F[λ]m×n ,如果 A ( λ ) A(\lambda) A(λ) 经过有限次多项式矩阵的初等变换可以化为 B ( λ ) B(\lambda) B(λ),则称 A ( λ ) A(\lambda) A(λ) 与 B ( λ ) B(\lambda) B(λ) 等价,记为 A ( λ ) ≃ B ( λ ) A(\lambda)\simeq B(\lambda) A(λ)≃B(λ)
【定理】元的降次化简
设 A ( λ ) = [ a i j ( λ ) ] m × n A(\lambda)=[a_{ij}(\lambda)]_{m\times n} A(λ)=[aij(λ)]m×n, a 11 ( λ ) ≠ 0 a_{11}(\lambda)\neq0 a11(λ)=0,如果 A ( λ ) A(\lambda) A(λ) 中至少有一个元不能被 a 11 ( λ ) a_{11}(\lambda) a11(λ) 除尽,则存在 B ( λ ) = [ b i j ( λ ) ] m × n B(\lambda)=[b_{ij}(\lambda)]_{m\times n} B(λ)=[bij(λ)]m×n,满足
- A ( λ ) ≃ B ( λ ) A(\lambda)\simeq B(\lambda) A(λ)≃B(λ)
- b 11 ( λ ) ≠ 0 b_{11}(\lambda)\neq0 b11(λ)=0,且 deg b 11 ( λ ) < deg a 11 ( λ ) \deg b_{11}(\lambda)<\deg a_{11}(\lambda) degb11(λ)<dega11(λ),其中 deg \deg deg 表示多项式的次数
具体化简操作分三种情况:
(1)第一列中存在元素不能被
a
11
(
λ
)
a_{11}(\lambda)
a11(λ) 除尽
[
a
11
(
λ
)
⋯
⋯
⋯
⋮
⋯
⋯
⋯
a
i
1
(
λ
)
⋮
⋮
⋯
⋯
⋯
⋯
]
\begin{bmatrix} a_{11}(\lambda) & \cdots & \cdots & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ a_{i1}(\lambda) & \vdots & & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
a11(λ)⋮ai1(λ)⋯⋯⋯⋮⋯⋯⋯⋯⋯⋯⋮⋯
利用多项式带余除法
a
i
1
(
λ
)
=
a
11
(
λ
)
q
(
λ
)
+
r
(
λ
)
a_{i1}(\lambda)=a_{11}(\lambda)q(\lambda)+r(\lambda)
ai1(λ)=a11(λ)q(λ)+r(λ)
⟶
[
r
(
λ
)
⋯
⋯
⋯
⋮
⋯
⋯
⋯
a
11
(
λ
)
⋮
⋮
⋯
⋯
⋯
⋯
]
\longrightarrow \begin{bmatrix} r(\lambda) & \cdots & \cdots & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ a_{11}(\lambda) & \vdots & & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
⟶
r(λ)⋮a11(λ)⋯⋯⋯⋮⋯⋯⋯⋯⋯⋯⋮⋯
(2)第一行中存在元素不能被
a
11
(
λ
)
a_{11}(\lambda)
a11(λ) 除尽
[
a
11
(
λ
)
⋯
a
1
i
(
λ
)
⋯
⋮
⋯
⋯
⋯
⋮
⋮
⋮
⋯
⋯
⋯
⋯
]
\begin{bmatrix} a_{11}(\lambda) & \cdots & a_{1i}(\lambda) & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ \vdots & \vdots & & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
a11(λ)⋮⋮⋯⋯⋯⋮⋯a1i(λ)⋯⋯⋯⋯⋮⋯
利用多项式带余除法
a
1
i
(
λ
)
=
a
11
(
λ
)
q
(
λ
)
+
r
(
λ
)
a_{1i}(\lambda)=a_{11}(\lambda)q(\lambda)+r(\lambda)
a1i(λ)=a11(λ)q(λ)+r(λ)
⟶
[
r
(
λ
)
⋯
a
11
(
λ
)
⋯
⋮
⋯
⋯
⋯
⋮
⋮
⋮
⋯
⋯
⋯
⋯
]
\longrightarrow \begin{bmatrix} r(\lambda) & \cdots & a_{11}(\lambda) & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ \vdots & \vdots & & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
⟶
r(λ)⋮⋮⋯⋯⋯⋮⋯a11(λ)⋯⋯⋯⋯⋮⋯
(3)第一行第一列中元素都能被
a
11
(
λ
)
a_{11}(\lambda)
a11(λ) 除尽,但存在
a
i
j
(
λ
)
a_{ij}(\lambda)
aij(λ) 不能被
a
11
(
λ
)
a_{11}(\lambda)
a11(λ) 除尽
[
a
11
(
λ
)
⋯
a
1
i
(
λ
)
⋯
⋮
⋯
⋯
⋯
a
i
1
(
λ
)
⋮
a
i
j
(
λ
)
⋮
⋯
⋯
⋯
⋯
]
\begin{bmatrix} a_{11}(\lambda) & \cdots & a_{1i}(\lambda) & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ a_{i1}(\lambda) & \vdots & a_{ij}(\lambda) & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
a11(λ)⋮ai1(λ)⋯⋯⋯⋮⋯a1i(λ)⋯aij(λ)⋯⋯⋯⋮⋯
有
a
i
1
(
λ
)
=
a
11
(
λ
)
φ
(
λ
)
a_{i1}(\lambda)=a_{11}(\lambda)\varphi(\lambda)
ai1(λ)=a11(λ)φ(λ),经过初等变换后有
[
a
11
(
λ
)
⋯
a
1
i
(
λ
)
⋯
⋮
⋯
⋯
⋯
0
⋮
a
i
j
(
λ
)
−
φ
(
λ
)
a
1
j
(
λ
)
⋮
⋯
⋯
⋯
⋯
]
\begin{bmatrix} a_{11}(\lambda) & \cdots & a_{1i}(\lambda) & \cdots \\ \vdots & \cdots & \cdots & \cdots \\ 0 & \vdots & a_{ij}(\lambda)-\varphi(\lambda)a_{1j}(\lambda) & \vdots \\ \cdots & \cdots & \cdots & \cdots \\ \end{bmatrix}
a11(λ)⋮0⋯⋯⋯⋮⋯a1i(λ)⋯aij(λ)−φ(λ)a1j(λ)⋯⋯⋯⋮⋯
【定理】等价标准型(史密斯标准型)
除零矩阵以外,都能通过初等变换(可以行列混合)变为标准型
有了降次化简之后,就可以将矩阵往标准型变换了(此处是“等价标准型”/“史密斯标准型”)
多项式矩阵的元通常按照降幂排列,即最高次项写在最前面
设 A ( λ ) = F [ λ ] m × n A(\lambda)=F[\lambda]^{m\times n} A(λ)=F[λ]m×n, A ( λ ) ≠ 0 A(\lambda)\neq0 A(λ)=0,则 A ( λ ) A(\lambda) A(λ) 等价于
[ d 1 ( λ ) d 2 ( λ ) ⋱ d r ( λ ) 0 ⋱ 0 ] m × n \begin{bmatrix} d_1(\lambda) \\ & d_2(\lambda) \\ && \ddots \\ &&& d_r(\lambda)\\ &&&& 0 \\ &&&&&\ddots \\ &&&&&& 0 \\ \end{bmatrix}_{m\times n} d1(λ)d2(λ)⋱dr(λ)0⋱0 m×n
其中 r ≥ 1 r\geq1 r≥1, d i ( λ ) d_i(\lambda) di(λ) 为首 1 多项式2,并且 d i ( λ ) ∣ d i + 1 ( λ ) ( i = 1 , 2 , ⋯ , r − 1 ) d_i(\lambda)\mid d_{i+1}(\lambda)(i=1,2,\cdots,r-1) di(λ)∣di+1(λ)(i=1,2,⋯,r−1)3
注意只有满足整除条件才算标准型,不然顶多是个对角阵
【定理】等价标准型(史密斯标准型)是唯一的
三、多项式矩阵的等价不变量
除了秩在初等变换中不会改变以外,还有 行列式因子;不变因子;初等因子 不会改变
【定理】初等变换不改变 行列式因子、不变因子、初等因子
如果两个多项式矩阵等价,则
- 他们具有相同的 各阶行列式因子
- 他们具有相同的 不变因子
- 他们具有相同的 秩与初等因子
【定义】行列式因子
设 A ( λ ) ∈ F [ λ ] m × n A(\lambda)\in F[\lambda]^{m\times n} A(λ)∈F[λ]m×n, r a n k A ( λ ) = r ≥ 1 rankA(\lambda)=r\geq1 rankA(λ)=r≥1,
- A ( λ ) A(\lambda) A(λ) 中全部 k k k 阶子式的首1最大公因式 D k ( λ ) D_k(\lambda) Dk(λ) 称为 A ( λ ) A(\lambda) A(λ) 的 k k k 阶行列式因子,( 1 ≤ k ≤ r 1\leq k\leq r 1≤k≤r)
以求如下矩阵的行列式因子为例
A
(
λ
)
=
[
1
−
λ
2
λ
−
1
λ
λ
λ
2
−
λ
1
+
λ
2
λ
3
+
λ
−
1
−
λ
]
⟶
[
1
λ
λ
2
+
λ
]
A(\lambda)= \begin{bmatrix} 1-\lambda & 2\lambda-1 & \lambda \\ \lambda & \lambda^2 & -\lambda \\ 1+\lambda^2 & \lambda^3+\lambda-1 & -\lambda \\ \end{bmatrix} \longrightarrow \begin{bmatrix} 1 \\ &\lambda \\ &&\lambda^2+\lambda \\ \end{bmatrix}
A(λ)=
1−λλ1+λ22λ−1λ2λ3+λ−1λ−λ−λ
⟶
1λλ2+λ
其1阶子式分别为
[
1
]
[1]
[1]、
[
λ
]
[\lambda]
[λ]、
[
λ
2
+
λ
]
[\lambda^2+\lambda]
[λ2+λ],这3个子式的行列式的最大公因子为 1,即1阶行列式因子为1
其3阶子式的行列式为
λ
(
λ
2
+
λ
)
\lambda(\lambda^2+\lambda)
λ(λ2+λ),所以其3阶行列式因子为
λ
(
λ
2
+
λ
)
\lambda(\lambda^2+\lambda)
λ(λ2+λ)
其2阶子式比较多(任选两行两列求行列式,一共9种)然后再找所有2阶子式的行列式的最大公因式,计算得到为
λ
\lambda
λ;
初等变换得到标准型后,可以得到2阶子式:
[
1
λ
]
,
[
1
λ
2
+
λ
]
,
[
λ
λ
2
+
λ
]
\begin{bmatrix} 1 \\ &\lambda \\ \end{bmatrix},\quad \begin{bmatrix} 1 \\ &\lambda^2+\lambda \\ \end{bmatrix},\quad \begin{bmatrix} \lambda \\ &\lambda^2+\lambda \\ \end{bmatrix}
[1λ],[1λ2+λ],[λλ2+λ]
可以更容易的看出2阶行列式因子为
λ
\lambda
λ
最终得到的结果为 D 1 ( λ ) = 1 D_1(\lambda)=1 D1(λ)=1, D 2 ( λ ) = λ D_2(\lambda)=\lambda D2(λ)=λ, D 3 ( λ ) = λ 3 + λ 2 D_3(\lambda)=\lambda^3+\lambda^2 D3(λ)=λ3+λ2
【定义】不变因子
A ( λ ) A(\lambda) A(λ) 的等价标准型种非零元
d 1 ( λ ) , d 2 ( λ ) , ⋯ , d r ( λ ) d_1(\lambda),d_2(\lambda),\cdots,d_r(\lambda) d1(λ),d2(λ),⋯,dr(λ)
称为 A ( λ ) A(\lambda) A(λ) 的不变因子
【定义】初等因子
将多项式矩阵的每一个非常数不变因子分解成互不相同的一次因式的方幂的乘积,所有这些一次因式的方幂(相同的必须按照出现的次数计算)称为多项式矩阵的初等因子
比如先通过初等变换得到对角矩阵:
A
(
λ
)
=
[
0
0
0
λ
2
0
0
λ
2
−
λ
0
0
(
λ
−
1
)
2
0
0
λ
2
−
λ
0
0
0
]
A(\lambda)= \begin{bmatrix} 0 & 0 & 0 & \lambda^2 \\ 0 & 0 & \lambda^2-\lambda & 0 \\ 0 & (\lambda-1)^2 & 0 & 0 \\ \lambda^2-\lambda & 0 & 0 & 0 \\ \end{bmatrix}
A(λ)=
000λ2−λ00(λ−1)200λ2−λ00λ2000
看其对角线上的每一项,其初等因子分别为:
- λ 2 \lambda^2 λ2 的初等因子是 λ 2 \lambda^2 λ2
- λ 2 − λ \lambda^2-\lambda λ2−λ 的初等因子是 λ \lambda λ, λ − 1 \lambda-1 λ−1
- ( λ − 1 ) 2 (\lambda-1)^2 (λ−1)2 的初等因子是 ( λ − 1 ) 2 (\lambda-1)^2 (λ−1)2
- λ 2 − λ \lambda^2-\lambda λ2−λ 的初等因子是 λ \lambda λ, λ − 1 \lambda-1 λ−1
所以 A ( λ ) A(\lambda) A(λ) 的全部初等因子为 λ 2 , λ , λ − 1 , ( λ − 1 ) 2 , λ , λ − 1 \lambda^2,\lambda,\lambda-1,(\lambda-1)^2,\lambda,\lambda-1 λ2,λ,λ−1,(λ−1)2,λ,λ−1
【定理】二阶复系数多项式的等价标准型
设 f i ( λ ) , g i ( λ ) ( i = 1 , 2 ) f_i(\lambda),g_i(\lambda)(i=1,2) fi(λ),gi(λ)(i=1,2) 为复系数多项式,并且满足
- ( f 1 ( λ ) , g 1 ( λ ) ) = ( f 1 ( λ ) , g 2 ( λ ) ) = 1 (f_1(\lambda),g_1(\lambda))=(f_1(\lambda),g_2(\lambda))=1 (f1(λ),g1(λ))=(f1(λ),g2(λ))=1
- ( f 2 ( λ ) , g 1 ( λ ) ) = ( f 2 ( λ ) , g 2 ( λ ) ) = 1 (f_2(\lambda),g_1(\lambda))=(f_2(\lambda),g_2(\lambda))=1 (f2(λ),g1(λ))=(f2(λ),g2(λ))=1
其中 ( f i ( λ ) , g j ( λ ) ) (f_i(\lambda),g_j(\lambda)) (fi(λ),gj(λ)) 表示二者的首1最大公因式,则
[ ( f 1 ( λ ) , g 1 ( λ ) ) ( f 2 ( λ ) , g 2 ( λ ) ) ] ≃ [ ( f 2 ( λ ) , g 1 ( λ ) ) ( f 1 ( λ ) , g 2 ( λ ) ) ] \begin{bmatrix} (f_1(\lambda),g_1(\lambda)) & \\ & (f_2(\lambda),g_2(\lambda)) \\ \end{bmatrix} \simeq \begin{bmatrix} (f_2(\lambda),g_1(\lambda)) & \\ & (f_1(\lambda),g_2(\lambda)) \\ \end{bmatrix} [(f1(λ),g1(λ))(f2(λ),g2(λ))]≃[(f2(λ),g1(λ))(f1(λ),g2(λ))]
【定理】初等因子与全部初等因子
设
A ( λ ) = [ A 1 ( λ ) A 2 ( λ ) ⋱ A ( λ ) ] A(\lambda)= \begin{bmatrix} A_1(\lambda) \\ & A_2(\lambda) \\ && \ddots \\ &&& A_(\lambda) \\ \end{bmatrix} A(λ)= A1(λ)A2(λ)⋱A(λ)
则 A 1 ( λ ) , A 2 ( λ ) , ⋯ , A s ( λ ) A_1(\lambda),A_2(\lambda),\cdots,A_s(\lambda) A1(λ),A2(λ),⋯,As(λ) 的初等因子的全体恰为 A ( λ ) A(\lambda) A(λ) 的全部初等因子
比如
A
(
λ
)
=
[
1
λ
λ
0
λ
0
0
λ
−
1
]
=
[
A
1
(
λ
)
0
0
A
2
(
λ
)
]
A(\lambda)= \begin{bmatrix} 1 & \lambda \\ \lambda & 0 \\ && \lambda & 0 \\ && 0 & \lambda-1 \\ \end{bmatrix}= \begin{bmatrix} A_1(\lambda) & 0 \\ 0 & A_2(\lambda) \\ \end{bmatrix}
A(λ)=
1λλ0λ00λ−1
=[A1(λ)00A2(λ)]
其初等因子为
λ
2
,
λ
,
λ
−
1
\lambda^2,\lambda,\lambda-1
λ2,λ,λ−1
【关系】行列式因子、不变因子、初等因子之间的互相求解
行列式因子 ⟺ \Longleftrightarrow ⟺ 不变因子 ⟺ \Longleftrightarrow ⟺ 秩 + 初等因子
化为对角矩阵(不一定非得是标准型), 初等因子 是最好求的
(1)不变因子 ⟺ \Longleftrightarrow ⟺ 秩 + 初等因子
将不变因子逐项进行因式分解即可得到初等因子;
初等因子 + 秩 推 不变因子参考下面两类限制:
对于初等因子带来的限制:
- 同一个一次因式的方幂应该出现在不同的不变因子中
- 幂最高的一个应该出现在最后一级不变因子中
- 余下的初等因子中方幂最高的应该出现在倒数第二级不变因子中,以此类推
对于不变因子带来的限制:
- 不变因子的整除特性
- 不变因子的首 1 特性
转换示例:
-
全部的初等因子为 λ , λ , λ − 1 , λ − 1 , λ 2 , ( λ − 1 ) 2 \lambda,\lambda,\lambda-1,\lambda-1,\lambda^2,(\lambda-1)^2 λ,λ,λ−1,λ−1,λ2,(λ−1)2 ;rank 为 4
对应的不变因子为 1 , λ ( λ − 1 ) , λ ( λ − 1 ) , λ 2 ( λ − 1 ) 2 1,\lambda(\lambda-1),\lambda(\lambda-1),\lambda^2(\lambda-1)^2 1,λ(λ−1),λ(λ−1),λ2(λ−1)2
-
全部的初等因子为 λ , λ , λ − 1 , λ − 1 , λ 2 , ( λ − 1 ) 2 \lambda,\lambda,\lambda-1,\lambda-1,\lambda^2,(\lambda-1)^2 λ,λ,λ−1,λ−1,λ2,(λ−1)2 ;rank 为 3
对应的不变因子为 λ ( λ − 1 ) , λ ( λ − 1 ) , λ 2 ( λ − 1 ) 2 \lambda(\lambda-1),\lambda(\lambda-1),\lambda^2(\lambda-1)^2 λ(λ−1),λ(λ−1),λ2(λ−1)2
-
全部的初等因子为 ( λ − 2 ) , ( λ − 1 ) 2 (\lambda-2),(\lambda-1)^2 (λ−2),(λ−1)2 ;rank 为 3
对应的不变因子为 1 , 1 , ( λ − 2 ) ( λ − 1 ) 2 1,1,(\lambda-2)(\lambda-1)^2 1,1,(λ−2)(λ−1)2
(2)行列式因子 ⟺ \Longleftrightarrow ⟺ 不变因子
d
k
(
λ
)
d_k(\lambda)
dk(λ) 表示
k
k
k 阶不变因子;
D
k
(
λ
)
D_k(\lambda)
Dk(λ) 表示第
k
k
k 个行列式因子。
d
r
(
λ
)
=
D
r
(
λ
)
D
r
−
1
(
λ
)
d_r(\lambda)=\frac{D_r(\lambda)}{D_{r-1}(\lambda)}
dr(λ)=Dr−1(λ)Dr(λ)
-
【det】determinant:行列式 ↩︎
-
【首1多项式】是指最高次项的系数是 1 ↩︎文章来源:https://www.toymoban.com/news/detail-808269.html
-
【|】这个符号表示可以整除。(这个式子表示 d i ( λ ) d_i(\lambda) di(λ) 可以整除 d i + 1 ( λ ) d_{i+1}(\lambda) di+1(λ),比如 d i ( λ ) = 1 d_i(\lambda)=1 di(λ)=1 时,可以整除任何一个多项式) ↩︎文章来源地址https://www.toymoban.com/news/detail-808269.html
到了这里,关于1.矩阵的三种不变因子的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!