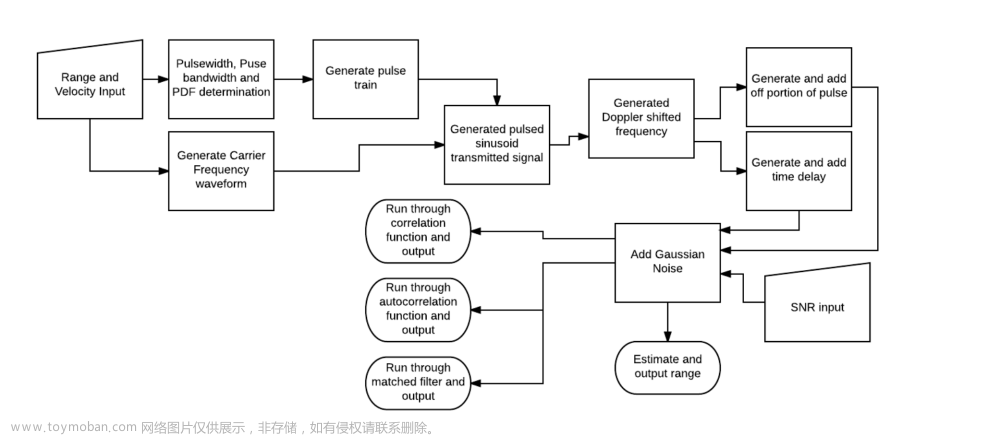
Matlab中利用FFT实现信号频谱搬移
在fft的理论中，fft的频移特性表示为：
也就是说，要想对信号f（t）实现频域的频谱搬移，只要在时域乘以一个矩阵，即可实现频谱的搬移。常用的振幅调制和解调就是如此，频谱搬移前后对比如下：
其特点就是仅频谱搬移，不产生新的频谱分量。利用欧拉公式：
e^(ix)=(cos x+isin x)
e^(ix)可以分解为实部和虚部，下面针对不同的搬移函数矩阵，对原始函数和频谱的影响分别介绍。
只有实部的频谱搬移
我们先构建一个原始函数：
A=220; %频率F1信号的幅度
F1=50; %信号1频率(Hz)
P1=-30; %信号1相位(度)
N=6400; %采样点数
t=[0:1/Fs:N/Fs]; %采样时刻 0到N个点
y_sin = A * (sin(2piF1t+piP1/180)); %// 50hz的正弦波信号
再构建频谱搬移矩阵函数，为频率1k的余弦波：
F2=1000
y2= cos(2*pi*F2*t)
则频谱搬移后函数的时域形式为：
S = y_sin .* y2;
分别对原始信号y_sin和S信号进行FFT变换，原始信号频谱图为：
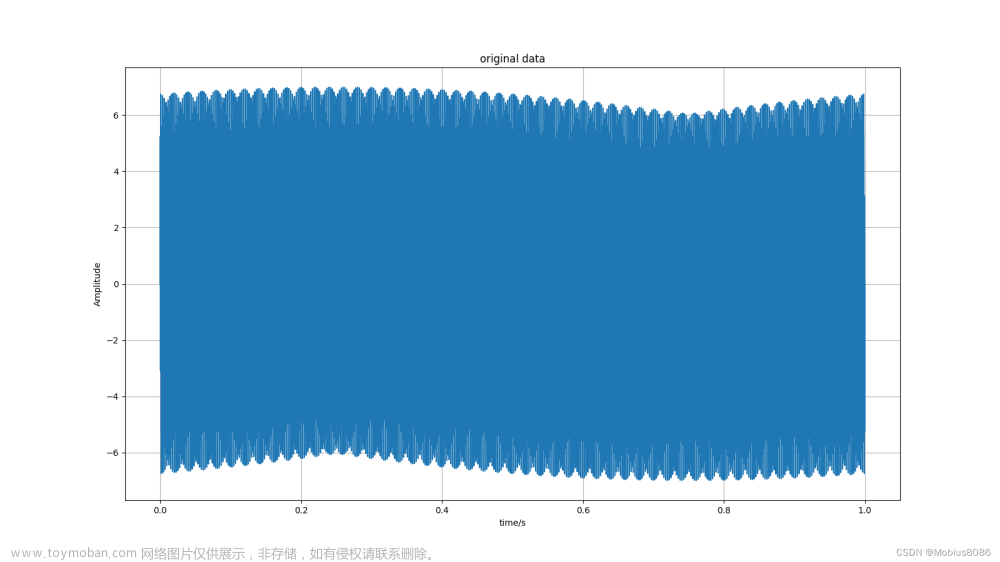
S信号在时域波形图为：
频谱搬移后频谱图为：
可以看出，已经实现了完整的频谱搬移。
只有虚部的频谱搬移
同样，构建频谱搬移矩阵函数只有虚部，频率1k：
y2= j*sin(2*pi*F2*t)
则频谱搬移后函数的时域形式为：
S = y_sin .* y2;
S信号在时域波形图为：
只有一个独立的冲击脉冲，是不是有点不可思议，我们对S做fft变换，得到S在频域下的频谱图为：
和只有实部的频谱图是一样的，是不是很神奇？
复函数下的频谱搬移
同样，构建频谱搬移矩阵函数为复函数，频率1k：
y2 = exp(j*2*pi*F2*t)
则频谱搬移后函数的时域形式为：
S = y_sin .* y2;
再次画出S的时域图：
咋一看，是不是有点画家出世的感觉，你能想想他的频谱图是怎么样的吗？事实上还是一样的，fft变换后，PPT如下图：文章来源：https://www.toymoban.com/news/detail-809074.html
综上所述，这三个频谱转移函数，功能上都实现了频谱的转移，但是区别在哪里昵？细心的朋友可能已经看出来了，在于幅度（或者说是能量损失），只有复函数的频谱搬移是没有能量损失的，是不是昵？欢迎朋友们一起讨论。文章来源地址https://www.toymoban.com/news/detail-809074.html
到了这里，关于Matlab中利用FFT实现信号频谱搬移的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
