Acwing-基础算法课笔记之搜索与图论-Toy模板网

这篇具有很好参考价值的文章主要介绍了Acwing-基础算法课笔记之搜索与图论。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

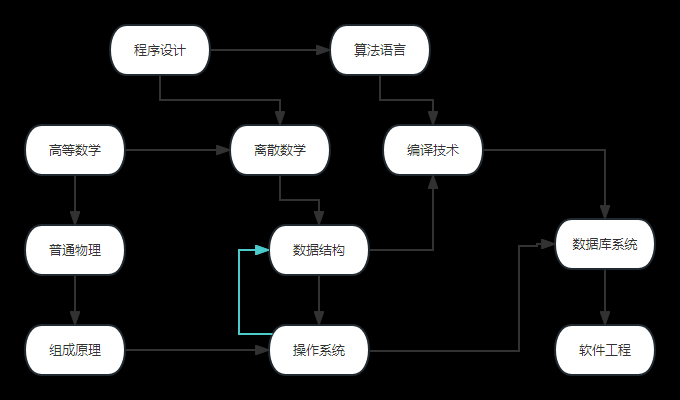
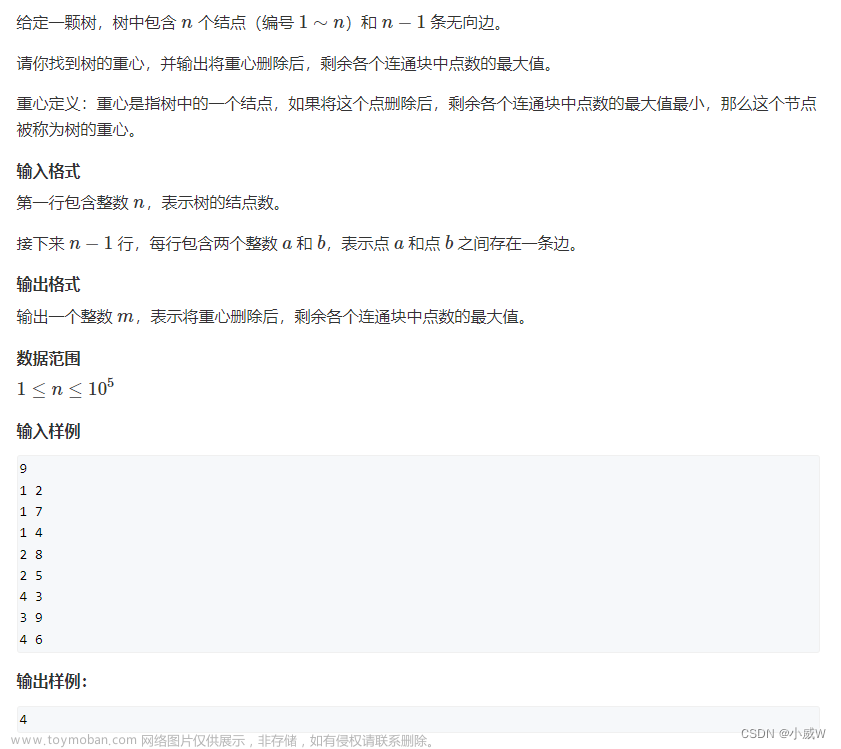
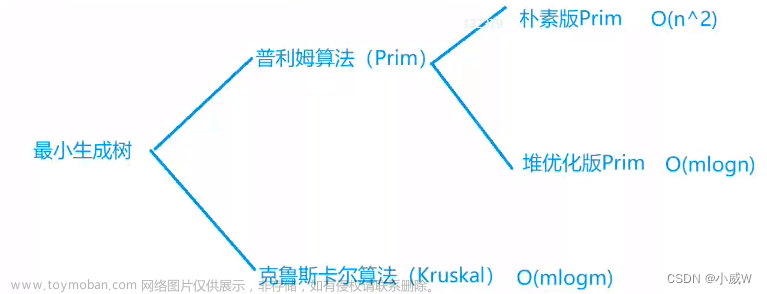
一、bellman-ford算法

1、概述

bellman-ford算法适用于负权边的图，求 1 到 n 的最多经过k条边的最短距离。
如图所示：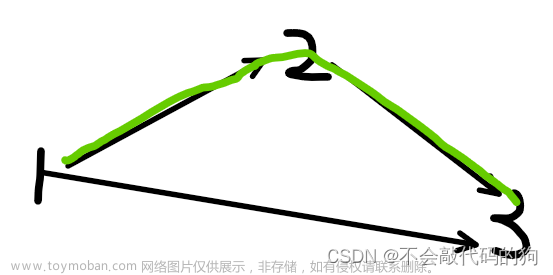
Acwing-基础算法课笔记之搜索与图论,Acwing基础算法课笔记,算法,笔记,图论

	1	2	3
dist	0	$\infty$	$\infty$

$\Downarrow$

	1	2	3
dist	0	1	$\infty$

$\Downarrow$

	1	2	3
dist	0	1	2

此过程中出现了串联的结果，所以是错误的，此时需要进行备份操作。

备份操作如下：

for(int i = 0; i < k; i++){
   memcpy(backup, dist, sizeof(dist);//backup存的是上一次迭代的结果
   for(int j = 0; j < m; j++){
      ..................
   }
}

2、特例

为了防止出现串联，保证符合题目条件，需要备份。
$注意：\textcolor{red}{bellman-ford算法中是不存在负权回路的}$

3、举例

bellman-ford算法的常规操作

for 循环遍历 n 次
   for 遍历所有边 a，b，w
      dist[b] = min(dist[b], dist[a] + w);
//此过程称为松弛操作

如图：
Acwing-基础算法课笔记之搜索与图论,Acwing基础算法课笔记,算法,笔记,图论
如果1 $\to$ a $\to$ b的距离比1 $\to$ b的短则更新dist[b]。
循环完之后，所有边的距离一定满足dist[b] $\le$ dist[a]+w，此不等式也称三角不等式。

4、bellman-ford算法模板

时间复杂度 $O (nm)$ ， $n$ 表示点数， $m$ 表示边数
注意在模板题中需要对下面的模板稍作修改，加上备份数组，详情见模板题。

int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离
struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];
// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }
    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}