Key Concept
熵权法是一种基于信息熵概念的权重确定方法,用于多指标决策分析中。信息熵是度量信息量的不确定性或混乱程度的指标,在熵权法中,它用来反映某个指标在评价过程中的分散程度,进而确定该指标的权重。指标的分散程度越高,信息熵越小,该指标的权重越大;反之,信息熵越大,权重越小。文章来源:https://www.toymoban.com/news/detail-810148.html
建模思路
-
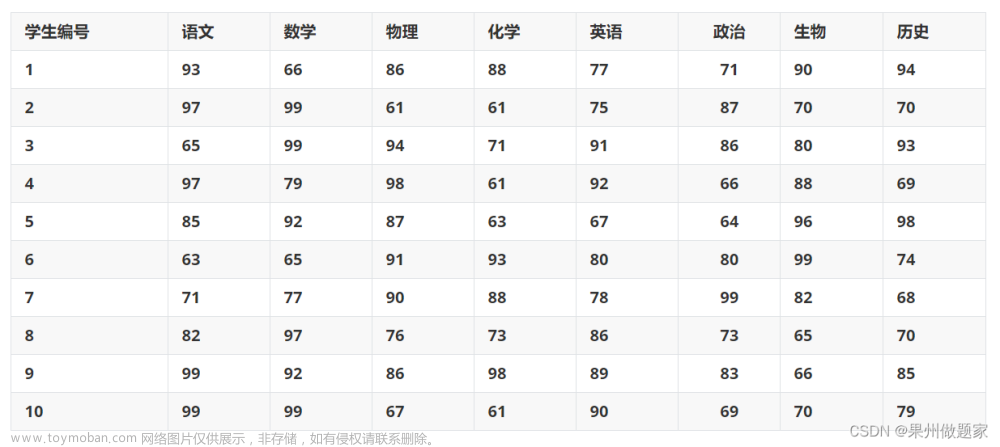
数据准备:
- 收集各个评价对象在不同指标下的原始数据。

- 收集各个评价对象在不同指标下的原始数据。
-
数据标准化正向化:
- 由于不同指标的量纲和数量级可能不同,需要对数据进行标准化处理,使其可比性增强。
#数据矩阵正向化 #将极小型数据转化为极大型数据 def minToMax(maxx,x): x=list(x) ans=[] for i in range(len(x)): ans.append(maxx-x[i]) return ans #将中间型数据转化为极大型数据 def midToMax(bestx,x): x=list(x) ans=[] h=[] #计算列表中每个元素与最优值的差的绝对值 for i in range (len(x)): h.append(abs(bestx-x[i])) M=max(h)#计算最大值,用来归一化 if M==0: M=1#防止除0错误 #计算每个元素的极大型值 for i in range(len(x)): ans.append(1-h[i]/M) return np.array(ans) #将区间型数据转化为极大型数据 def intervalToMax(x,lowx,highx): x=list(x) ans=[] for i in range(len(x)): if x[i]>=lowx and x[i]<=highx: ans.append(1) elif x[i]<lowx: ans.append(1-(lowx-x[i])/(lowx-min(x))) elif x[i]>highx: ans.append(1-(x[i]-highx)/max(x)-highx) return np.array(ans) #对数据矩阵进行标准化 def normalize(data): data=np.array(data) X=data/np.sqrt(np.sum(data**2,axis=0)) return X #对数据矩阵进行归一化 def regularize(data): data=np.array(data) m,n = np.shape(data) for i in range(n): col_sum=np.sum(data[:,i]) for j in range(m): data[j,i]=data[j,i]/col_sum return data 文章来源地址https://www.toymoban.com/news/detail-810148.html
文章来源地址https://www.toymoban.com/news/detail-810148.html
- 由于不同指标的量纲和数量级可能不同,需要对数据进行标准化处理,使其可比性增强。
-
计算指标的比重:
- 对于每个指标,计算每个评价对象在该指标下的比重,这通常是指标值除以该指标所有值的总和,这里其实就是进行归一化处理

- 对于每个指标,计算每个评价对象在该指标下的比重,这通常是指标值除以该指标所有值的总和,这里其实就是进行归一化处理
-
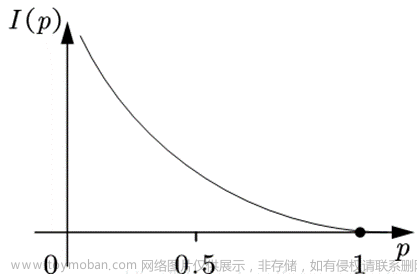
计算信息熵:
- 使用信息熵公式计算每个指标的信息熵。

- 使用信息熵公式计算每个指标的信息熵。
-
计算权值
-
计算得分
到了这里,关于MCM备赛笔记——熵权法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!