【算法基础】(一)基础算法 --- 归并排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法基础】(一)基础算法 --- 归并排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

✨个人主页：bit me
✨当前专栏：算法基础
🔥专栏简介：该专栏主要更新一些基础算法题，有参加蓝桥杯等算法题竞赛或者正在刷题的铁汁们可以关注一下🌹 🌹 🌹

💤一.归并排序（分治）

题目要求：

给定你一个长度为 n 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式：

输入共两行，第一行包含整数 n。

第二行包含 n 个整数（所有整数均在 1∼10^9 范围内），表示整个数列。

输出格式：

输出共一行，包含 n 个整数，表示排好序的数列。

数据范围：

1≤n≤100000

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

快排思路：

确定分界点：mid = (l + r) / 2

递归排序left，right

归并 —— 合二为一

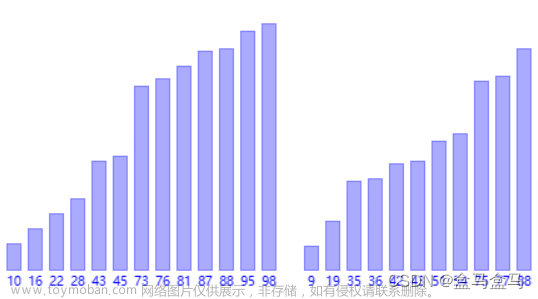
导图：

归并排序在算法里基础吗,算法基础,算法,排序算法,蓝桥杯,java,数据结构

首先我们需要设置下数据的范围，然后两个创建数组来方便我们后续使用，一个数组用来读取输入元素个数，一个数组用来临时归并合二为一

private static final int N = 100000 + 6;
private static int[] q = new int[N];
private static int[] t = new int[N];

数据的读取输入

BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
String str = input.readLine();
int n=Integer.parseInt(str);
String[] strs = input.readLine().split(" ");
for (int i = 0; i < n; i++) {
    q[i] = Integer.parseInt(strs[i]);
}

注意：在这里用BufferedReader是要比Scanner要好的，速度更快一点

然后排序函数代入，排序函数的实现

if (l >= r) return;
int mid = l + r >> 1;
sort(q, l, mid);
sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r) {
    if (q[i] <= q[j]) {
        t[k++] = q[i++];
    }
    else {
        t[k++] = q[j++];
    }
}
while (i <= mid) {
    t[k++] = q[i++];
}
while (j <= r) {
    t[k++] = q[j++];
}
for (i = l, j = 0; i <= r; i++, j++) {
    q[i] = t[j];
}

当左极值点大于等于右极值点，说明只有一个元素或者没有，直接返回

让分界点mid直接等于中点值

分界点mid俩边区域分别进行递归排序，数组名，起点和终点

两个指针i和j，分别从左边和中间开始往后走，分别比较元素大小，小的就纳入数组t中，直到有一个区域指针走完了，然后直接把另外的一个区域后面的衔接到数组t后面，就完成了排序

最后把t数组中的结果重新归并到数组q中

附上总的代码文章来源地址https://www.toymoban.com/news/detail-810457.html

public class TestDemo {
    private static final int N = 100000 + 6;
    private static int[] q = new int[N];
    private static int[] t = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader input = new BufferedReader(new InputStreamReader(System.in));
        String str = input.readLine();
        int n=Integer.parseInt(str);
        String[] strs = input.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            q[i] = Integer.parseInt(strs[i]);
        }
        sort(q, 0, n - 1);
        for (int i = 0; i < n; i++){
            System.out.printf("%d ", q[i]);
        }
    }

    private static void sort(int[] q, int l, int r) {
        if (l >= r) return;
        int mid = l + r >> 1;
        sort(q, l, mid);
        sort(q, mid + 1, r);
        int k = 0, i = l, j = mid + 1;
        while (i <= mid && j <= r) {
            if (q[i] <= q[j]) {
                t[k++] = q[i++];
            }
            else {
                t[k++] = q[j++];
            }
        }
        while (i <= mid) {
            t[k++] = q[i++];
        }
        while (j <= r) {
            t[k++] = q[j++];
        }
        for (i = l, j = 0; i <= r; i++, j++) {
            q[i] = t[j];
        }
    }
}

💨二.逆序对的数量

题目要求：

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式：

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式：

输出一个整数，表示逆序对的个数。

数据范围：

1≤n≤100000，
数列中的元素的取值范围 [1,10^9]。

输入样例：

6
2 3 4 5 6 1

输出样例：

5

结合归并排序：

[L,R] => [L,mid] + [mid+1,R]

递归排序[L,mid]和[mid+1,R]

归并，将左右两个有序序列合并成一个有序序列

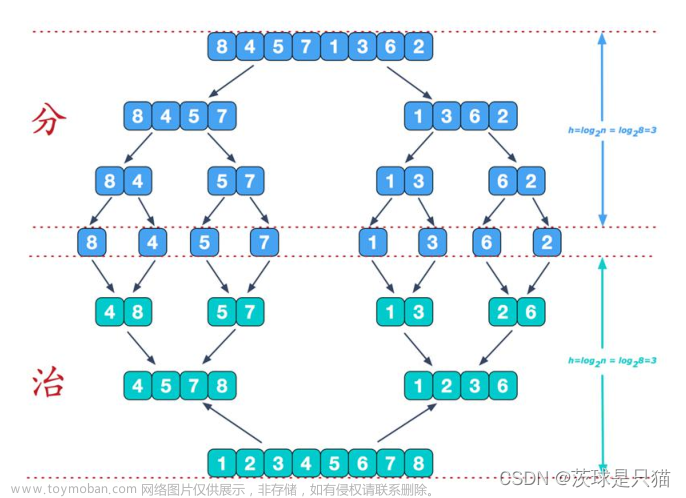
导图：

归并排序在算法里基础吗,算法基础,算法,排序算法,蓝桥杯,java,数据结构

我们可以继续分治：

整个区间的逆序数对分为左区间的逆序数对，右区间逆序数对和两个区间各组成的逆序数对，其中左区间和右区间的逆序对数量很直观，重点在于两者各取其一组成的逆序对怎么求

左区域逆序对数量：merge_sort(L,mid)
右区域逆序对数量：merge_sort(mid+1,R)
由归并排序我们可以知道左右俩区域都是按顺序来排列的，那么我们只需要找到左区域第一个大于右区域的最小数，那么它后面的数都是大于右区域的那个数字的，我们不妨设左区域那个元素下标为i，所以我们需要统计的个数是 mid - i + 1，恰巧在归并排序的合并过程中正好有两边序列依次比大小的过程
if (a[i] <= a[j]) tem[k++] = a[i++]; else { tem[k++] = a[j++]; }
else中的语句即代表左边数列中的数大于右边中的数了，我们可以在此时将mid-i+1加到总答案中去if (a[i] <= a[j]) tem[k++] = a[i++]; else { res += mid - i + 1; tem[k++] = a[j++]; }
问题解决后，我们的函数还没有解决问题的能力，只需要在递归出口的时候return 0;因为递归结束的时候数列中只有一个数了，不存在逆数对。还需要在递归归并排序的时候统计两边的逆序对数量之和long res = mergeSort(a, l, mid) + mergeSort(a, mid + 1, r);即可。

注意：题目中的数据范围最大是100000,一般对于数据范围大于10w的题目就要考虑数据溢出、时间复杂度等问题

当数列是一个倒序的数列时应该是逆序对数量最大的时候，每一个数可以和他后面所有的数形成逆数对，如果有n个数，那么总的逆序对数量为：(n-1)+(n-2)+……+1即n(n−1)/2个，大约n^2 / 2个，代入10w的数据范围得最多逆数对个数为：5×10 ^ 9，这个数据大于int的范围。所以这个题用int的话会溢出，我们采用long来存结果

附上总的代码

public class Main {
    public static void main(String[] args)  {
        Scanner scanner = new Scanner(new InputStreamReader(System.in));
        int n = scanner.nextInt();
        int[] a = new int[n];
        for (int i = 0; i < n; i++) {
            a[i] = scanner.nextInt();
        }
        System.out.println(merge_Sort(a, 0, n - 1));
        scanner.close();
    }

    private static long merge_Sort(int[] a, int l, int r) {
        if (l >= r){
            return 0;
		}
        int mid = l + r >> 1;
        long res = merge_Sort(a, l, mid) + merge_Sort(a, mid + 1, r);
        int tmp[] = new int[r-l+1];
        int k = 0, i = l, j = mid + 1;
        while (i <= mid && j <= r) {
            if (a[i] <= a[j]){
                tmp[k++] = a[i++];
            }else {
                res += mid - i + 1;
                tmp[k++] = a[j++];
            }
        }
        while (i <= mid){
            tmp[k++] = a[i++];
        }
        while (j <= r){
            tmp[k++] = a[j++];
        }
        for(i=l,j=0;i<=r;i++,j++){
        	a[i]=tmp[j];
        }
        return res;
    }
}