一.前言
机器学习的经典实验,对于数据集进行分类,网上看了一点其他的和GPT写的,好像只展示了4个特征中两个特征与3种类别的分类图,在我做这个实验交报告时,老师就问这个特征之间有很多交叉的点,在线性模型不应该得到分类准确度接近1的效果,后面改进加上另外两个特征的分类图可以发现,另外两个特征和类别有非常明显的线性关系,且分类的界限也非常清晰,所以模型分类准确度是合理的。下面主要是代码分享,给有这个学习需求或者课程实验的朋友们提供这个代码来学习或者参考。
二.实验要求
相当于我下面展示的代码的实现功能了
1.鸢尾花数据集准备与理解,并对数据集进行可视化分析;
2.随机划分数据集,80%样本作为训练数据,20%样本作为测试数据;
4.用训练数据分别训练以下2种SVM模型:
线性SVM模型
基于RBF的非线性SVM模型
5.分别对上述2种模型进行调优,性能指标为分类准确度﹔
6.测试上述2种模型在测试集上的分类性能。
三.说明
3.1.需导入的库
1.pandas
2.matplotblib
3.sklearn(安装时使用全称:scikit-learn)
全部都使用pip安装命令即可,简单快捷
win+R,输入cmd回车,pip命令【后面是镜像,不加速度非常慢】:
pip install 库名 -i https://pypi.doubanio.com/simple
3.2.数据集特征说明
这里使用的数据集是sklearn内置的数据集,不需要再下载数据集
load_iris()数据集包含了150个样本,每个样本有4个特征,分别是:
- 花萼长度(sepal length)
- 花萼宽度(sepal width)
- 花瓣长度(petal length)
- 花瓣宽度(petal width)
。这4个特征的单位均为厘米。这个数据集是鸢尾花数据集(Iris dataset)的一部分,共有3个不同的鸢尾花种类,每个种类有50个样本。3种鸢尾花的种类分别是:
- 0:Setosa(山鸢尾)
- 1:Versicolour(杂色鸢尾)
- 2:Virginica(维吉尼亚鸢尾)
四.代码分享
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
# 导入数据,分离特征与输出
iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
target = pd.Series(iris.target)
print('特征和目标的大小', iris_df.shape, target.shape)
# 画布属性设置
mpl.rcParams['font.family'] = ['sans-serif']
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 散点图
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
scatter = plt.scatter(iris_df.iloc[:, 0], iris_df.iloc[:, 1], c=target, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('鸢尾花特征分析散点图')
a, b = scatter.legend_elements()
print('散点对象及其标签', a, b)
b = ['setosa', 'versicolor', 'virginica'] # 原标签0,1,2分别对应以下三种
plt.legend(a, b)
plt.subplot(1, 2, 2)
scatter = plt.scatter(iris_df.iloc[:, 2], iris_df.iloc[:, 3], c=target, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('鸢尾花特征分析散点图')
a, b = scatter.legend_elements()
print('散点对象及其标签', a, b)
b = ['setosa', 'versicolor', 'virginica'] # 原标签0,1,2分别对应以下三种
plt.legend(a, b)
plt.show()
# 划分训练和测试数据
X_train, X_test, y_train, y_test = train_test_split(iris_df, target, test_size=0.2, random_state=5)
# 线型SVM模型训练
linear_svm = SVC(kernel='linear', C=1, random_state=0)
linear_svm.fit(X_train, y_train)
# 基于RBF非线性SVM模型训练
rbf_svm = SVC(kernel='rbf', C=1, gamma=0.1, random_state=0)
rbf_svm.fit(X_train, y_train)
# 模型评估
linear_y_pred = linear_svm.predict(X_test)
linear_accuracy = accuracy_score(y_test, linear_y_pred)
rbf_y_pred = rbf_svm.predict(X_test)
rbf_accuracy = accuracy_score(y_test, rbf_y_pred)
print()
print('线性SVM模型模型评估:')
print('参数C:', linear_svm.C)
print('分类准确度accuracy: ', linear_accuracy)
print()
print('RBF非线性SVM模型评估:')
print('参数C:{:d},gamma:{:.1f}'.format(rbf_svm.C, rbf_svm.gamma))
print('分类准确度accuracy: ', rbf_accuracy)
# print('真实分类:', list(y_test))
# print('预测分类', list(linear_y_pred))
# 线型模型分类结果展示
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=y_test, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('真实散点图')
plt.subplot(2, 2, 2)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=linear_y_pred, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('预测散点图')
plt.subplot(2, 2, 3)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=y_test, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('真实散点图')
plt.subplot(2, 2, 4)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=linear_y_pred, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('预测散点图')
plt.suptitle('线性模型分类结果对照图')
plt.show()
# rbf非线型模型分类结果展示
plt.figure(figsize=(8, 8))
plt.subplot(2, 2, 1)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=y_test, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('真实散点图')
plt.subplot(2, 2, 2)
plt.scatter(X_test.iloc[:, 0], X_test.iloc[:, 1], c=rbf_y_pred, cmap='viridis')
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('预测散点图')
plt.subplot(2, 2, 3)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=y_test, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('真实散点图')
plt.subplot(2, 2, 4)
plt.scatter(X_test.iloc[:, 2], X_test.iloc[:, 3], c=rbf_y_pred, cmap='viridis')
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('预测散点图')
plt.suptitle('rbf非线性模型分类结果对照图')
plt.show()
# 参数调优
print()
print('模型调优')
linear_params = {'C': [0.1, 0.5, 1, 5, 10]}
linear_gridsearch = GridSearchCV(SVC(kernel='linear'), linear_params, scoring='accuracy', cv=5)
linear_gridsearch.fit(X_train, y_train)
print('线性SVM参数调优结果:', linear_gridsearch.best_params_)
linear_svm.C = linear_gridsearch.best_params_['C']
rbf_params = {'C': [0.1, 0.5, 1, 5, 10], 'gamma': [0.001, 0.01, 0.1, 1, 10]}
rbf_gridsearch = GridSearchCV(SVC(kernel='rbf'), rbf_params, cv=5)
rbf_gridsearch.fit(X_train, y_train)
print('RBF非线性SVM参数调优结果:', rbf_gridsearch.best_params_)
rbf_svm.C = rbf_gridsearch.best_params_['C']
rbf_svm.gamma = rbf_gridsearch.best_params_['gamma']
# 模型评估
linear_y_pred = linear_svm.predict(X_test)
linear_accuracy = accuracy_score(y_test, linear_y_pred)
rbf_y_pred = rbf_svm.predict(X_test)
rbf_accuracy = accuracy_score(y_test, rbf_y_pred)
print()
print('参数调优后的模型性能:')
print('C:', linear_svm.C)
print('线性SVM模型准分类确度: ', linear_accuracy)
print('C,gamma:', rbf_svm.C, rbf_svm.gamma)
print('RBF非线性SVM模型准分类确度: ', rbf_accuracy)
五.结果展示
输出:
参数调优可以看到并没有增加分类准确度,调优在于使得模型训练能更快收敛。同时也可以看出非线性模型的分类效果比线性模型好一点
线性SVM模型模型评估:
参数C: 1
分类准确度accuracy: 0.9333333333333333RBF非线性SVM模型评估:
参数C:1,gamma:0.1
分类准确度accuracy: 0.9666666666666667模型调优
线性SVM参数调优结果: {'C': 0.5}
RBF非线性SVM参数调优结果: {'C': 5, 'gamma': 0.1}参数调优后的模型性能:
C: 0.5
线性SVM模型准分类确度: 0.9333333333333333
C,gamma: 5 0.1
RBF非线性SVM模型准分类确度: 0.9666666666666667Process finished with exit code 0
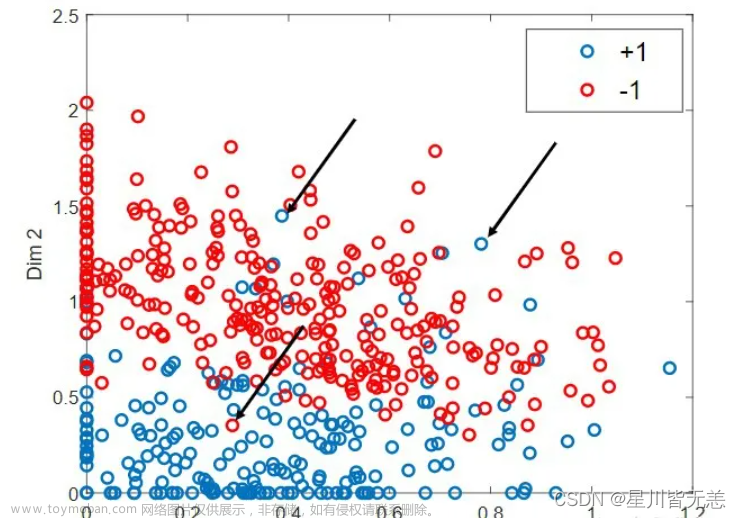
第一张图是4个特征与3种分类的散点图,一张图就描述两个特征,可以看到前两个特征来对花进行分类的话,ve,vi两类有很多交叉,分类是会产生误差的,但是后面两个特征与类别有明显线性关系,有清晰的分界线,除了少量点落在分界线附件可能产生错误分类,基本不会出现错误分类。

下面二张图是线性分类模型和rbf非线性模型训练后的预测对照图,分类准确度都超过90%,其实是故意用随机数种子得到的,改一下种子可以得到100%,因为特征与分类有明显线性关系,所以如果对数据集划分训练集和测试集时,测试集刚刚好没有被划分到在交界处的点,则分类可达100,都是正确的。

 文章来源:https://www.toymoban.com/news/detail-810576.html
文章来源:https://www.toymoban.com/news/detail-810576.html
六.后言
代码还有些地方待优化,但问题不大,懒得改了。嘿嘿文章来源地址https://www.toymoban.com/news/detail-810576.html
到了这里,关于Python鸢尾花SVM分类模型代码的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!