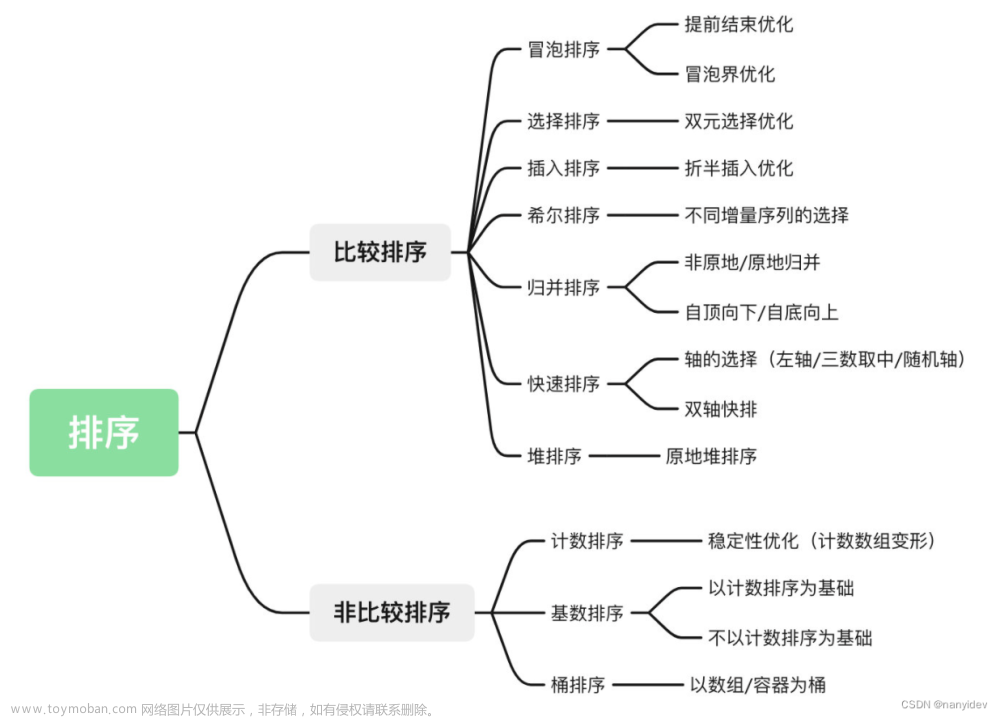
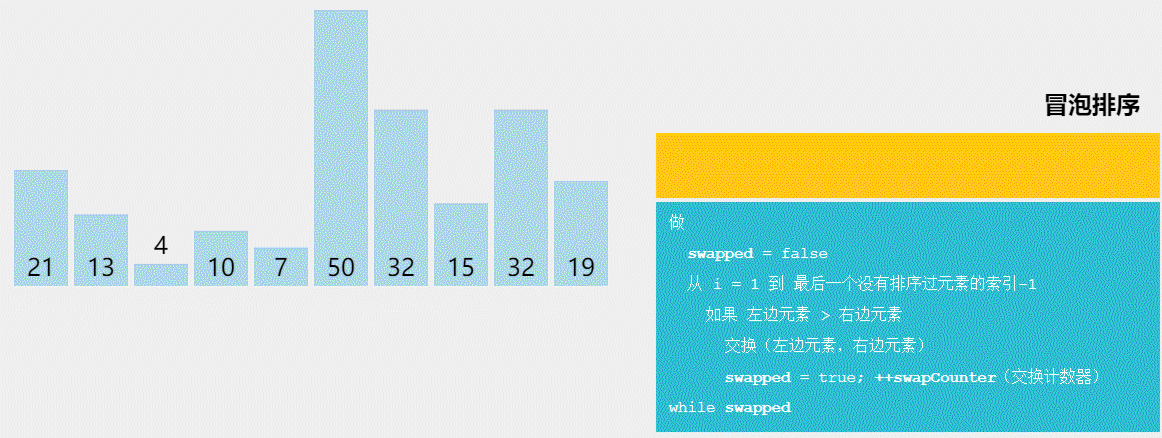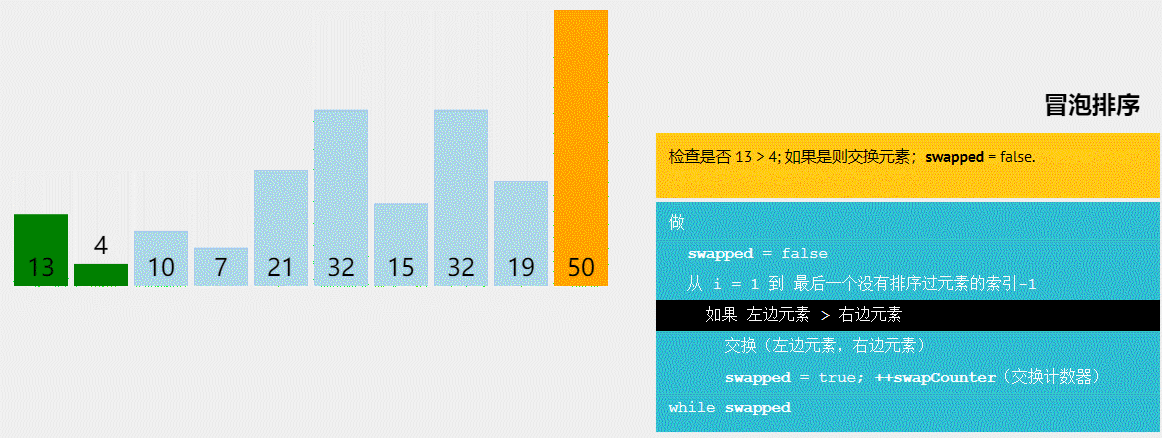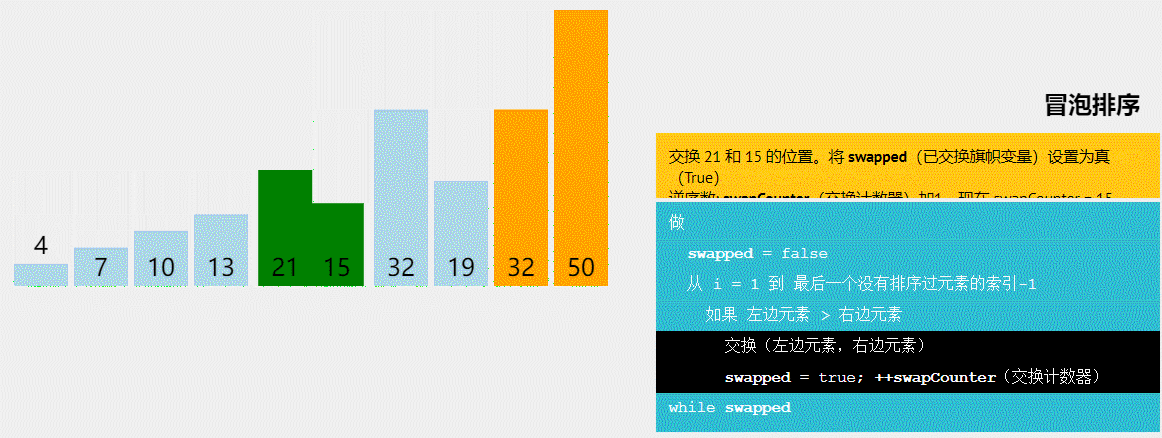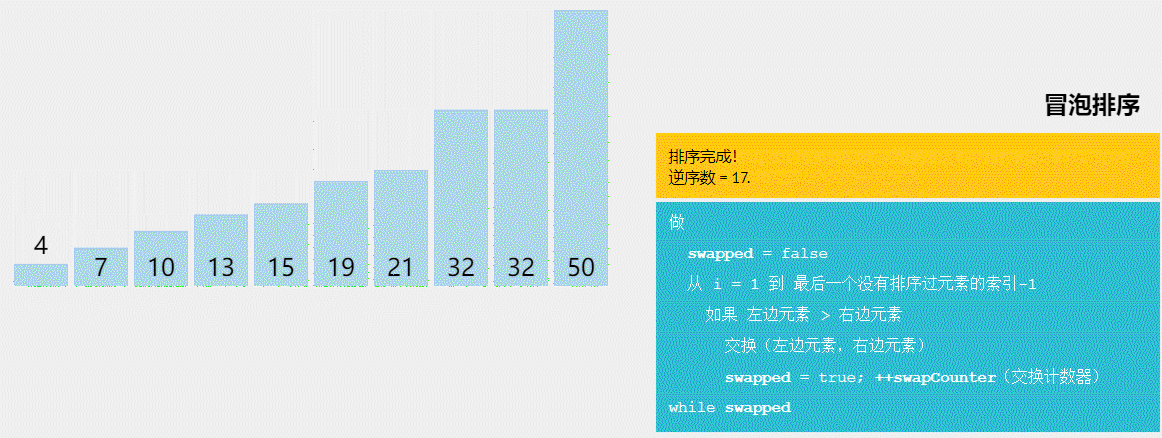C# 十大排序算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了C# 十大排序算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

以下是常见的十大排序算法（按照学习和实现的顺序排列）：

冒泡排序（Bubble Sort）
选择排序（Selection Sort）
插入排序（Insertion Sort）
希尔排序（Shell Sort）
归并排序（Merge Sort）
快速排序（Quick Sort）
堆排序（Heap Sort）
计数排序（Counting Sort）
桶排序（Bucket Sort）
基数排序（Radix Sort）

这些排序算法具有不同的时间复杂度、空间复杂度和稳定性，适用于不同的排序场景。每种算法都有其独特的思想和实现方式，您可以根据具体的需求选择适合的排序算法。

C#实现的十大排序算法的示例代码如下：

1、冒泡排序（Bubble Sort）:
class BubbleSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
2、选择排序（Selection Sort）:
class SelectionSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;

for (int i = 0; i < n - 1; i++)
{
int minIndex = i;
for (int j = i + 1; j < n; j++)
{
if (arr[j] < arr[minIndex])
{
minIndex = j;
}
}

int temp = arr[minIndex];
arr[minIndex] = arr[i];
arr[i] = temp;
}
}
}
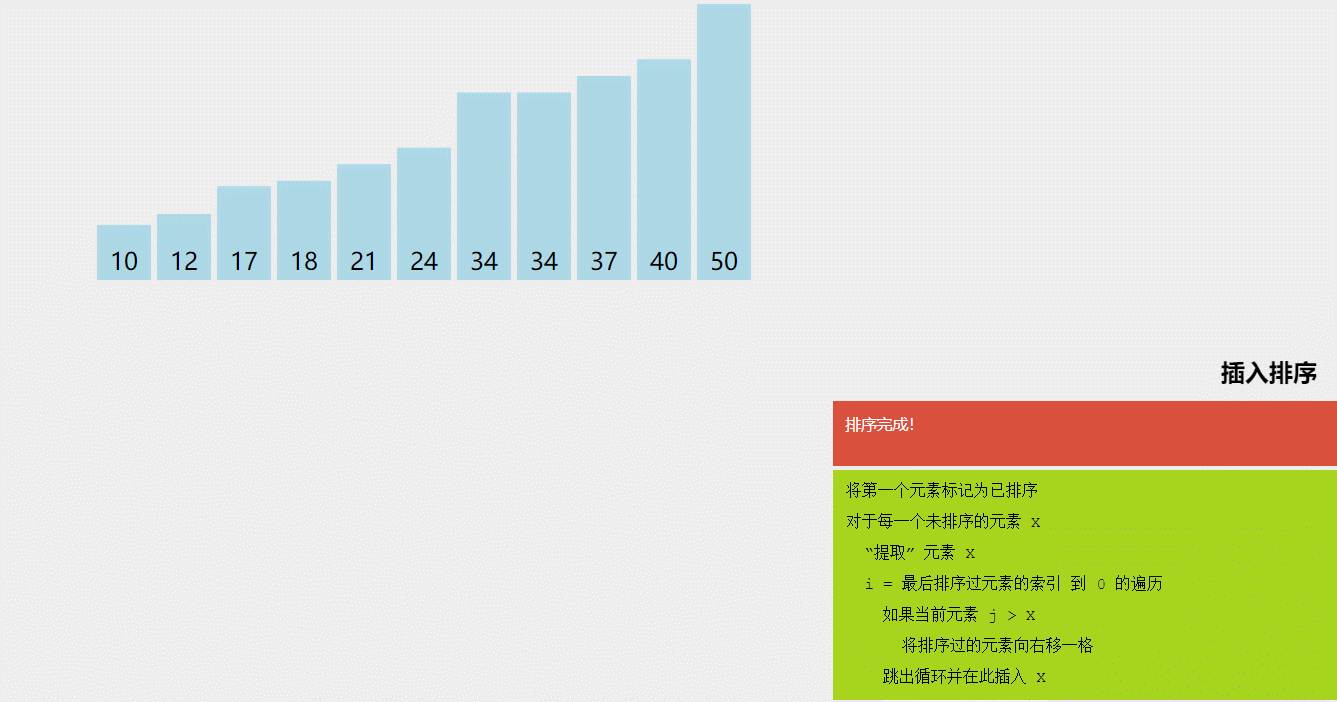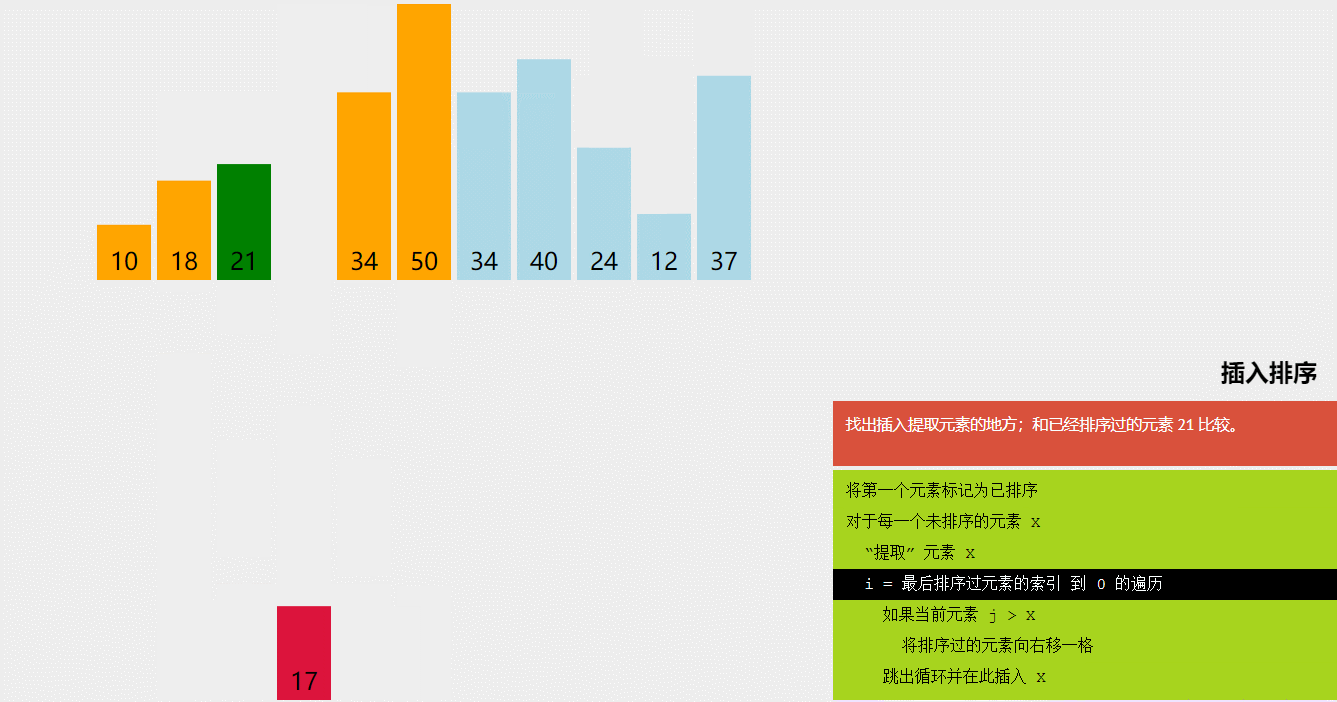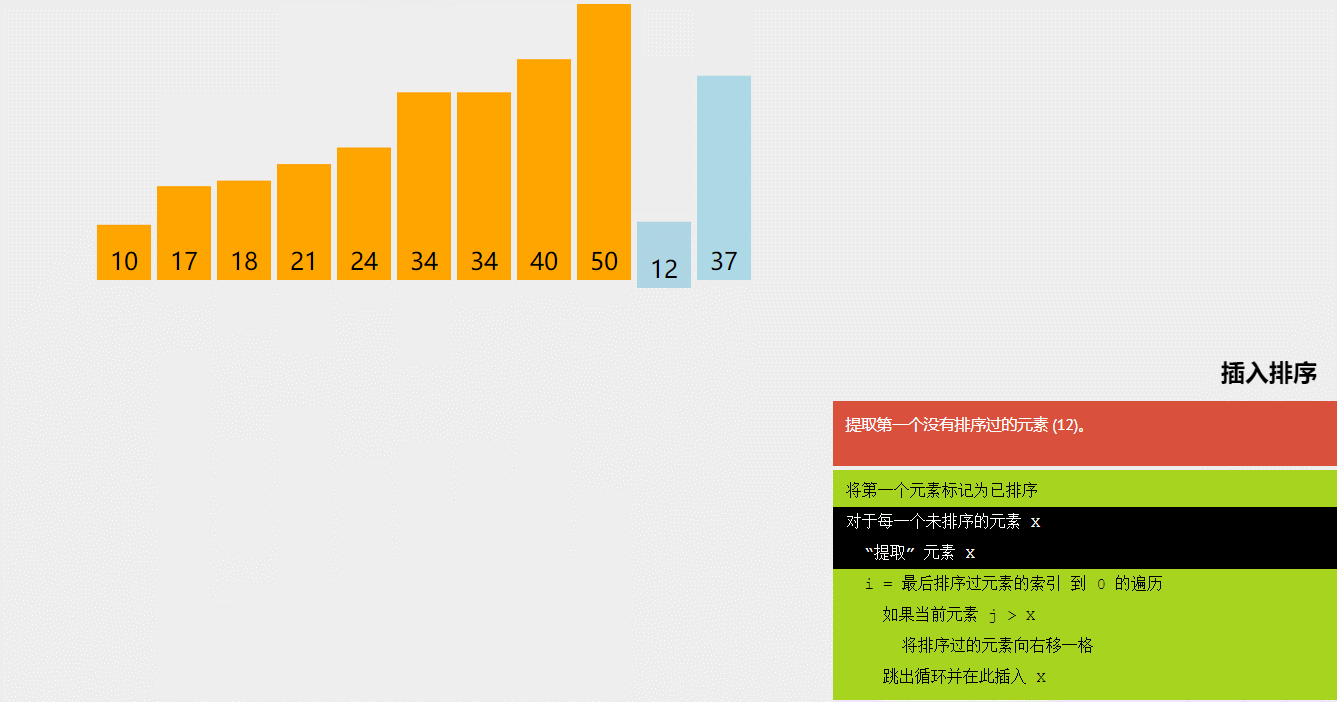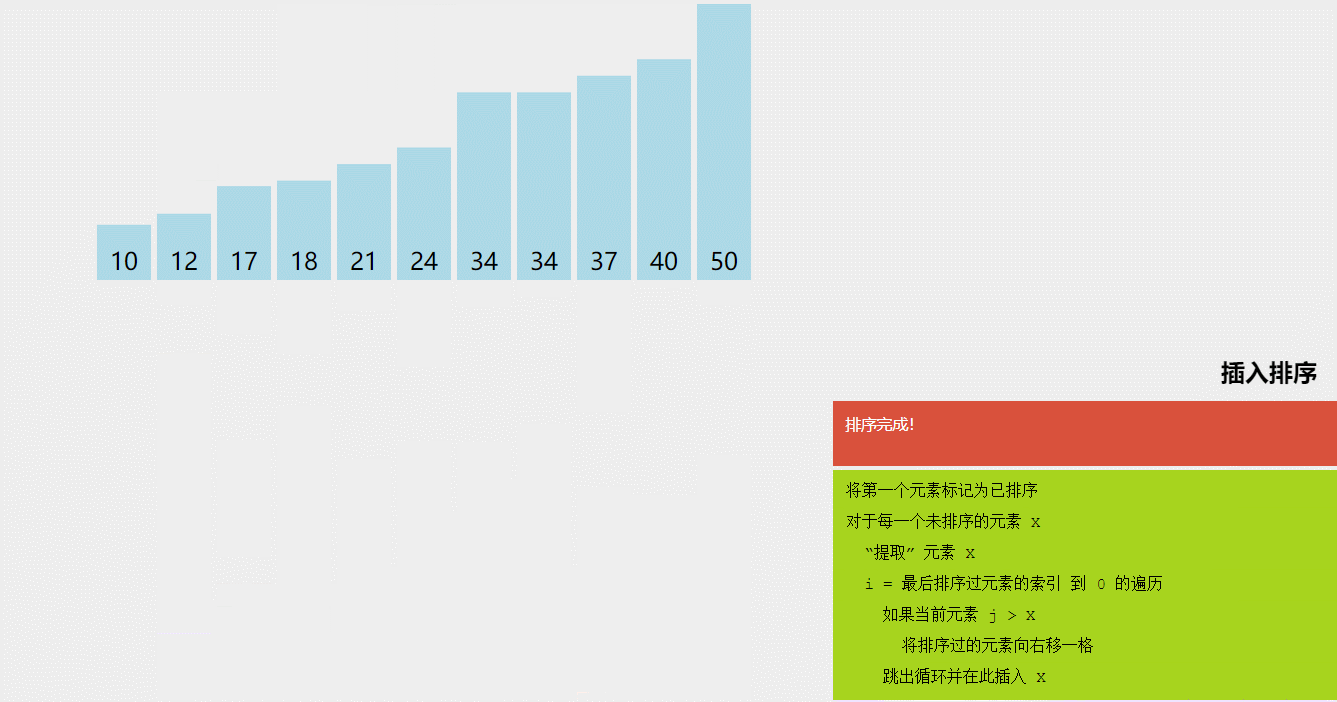
3、插入排序（Insertion Sort）:
class InsertionSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;
for (int i = 1; i < n; ++i)
{
int key = arr[i];
int j = i - 1;

while (j >= 0 && arr[j] > key)
{
arr[j + 1] = arr[j];
j = j - 1;
}

arr[j + 1] = key;
}
}
}
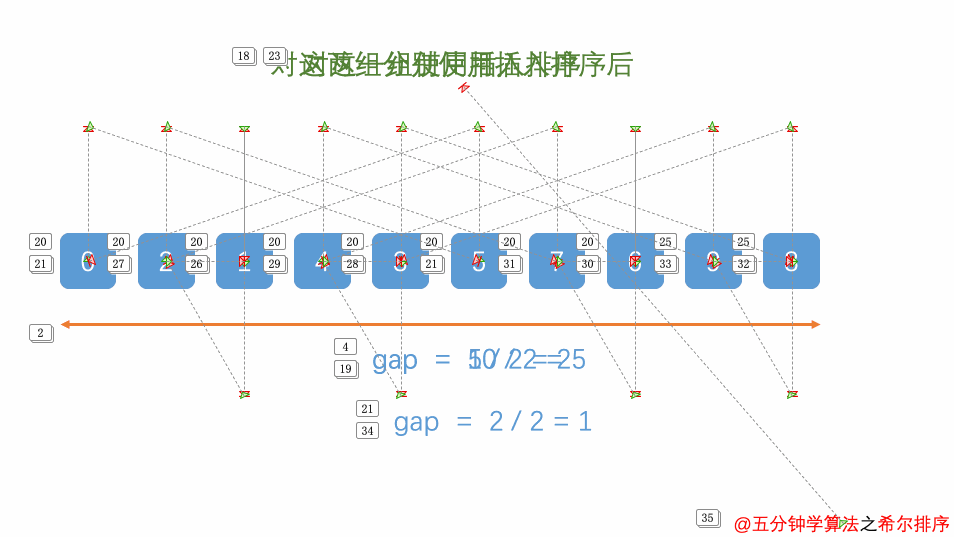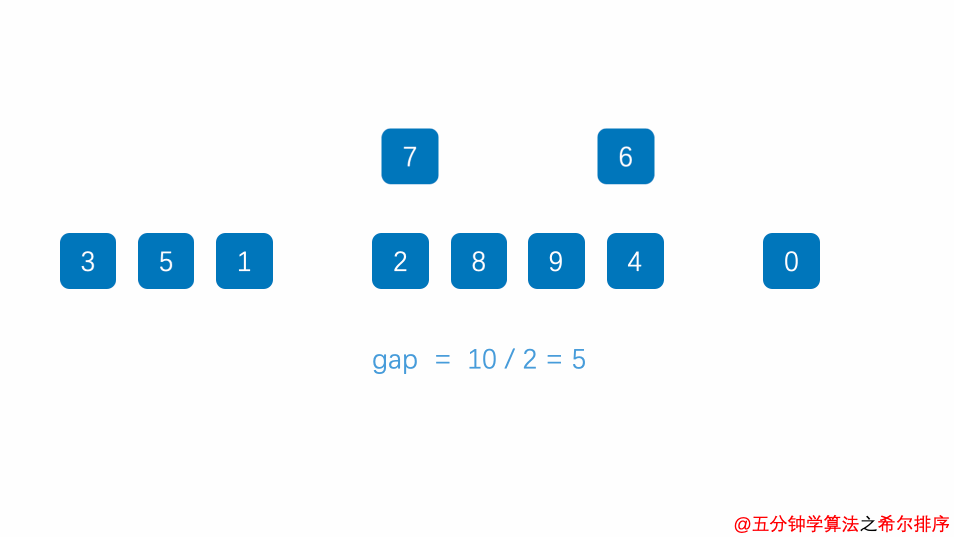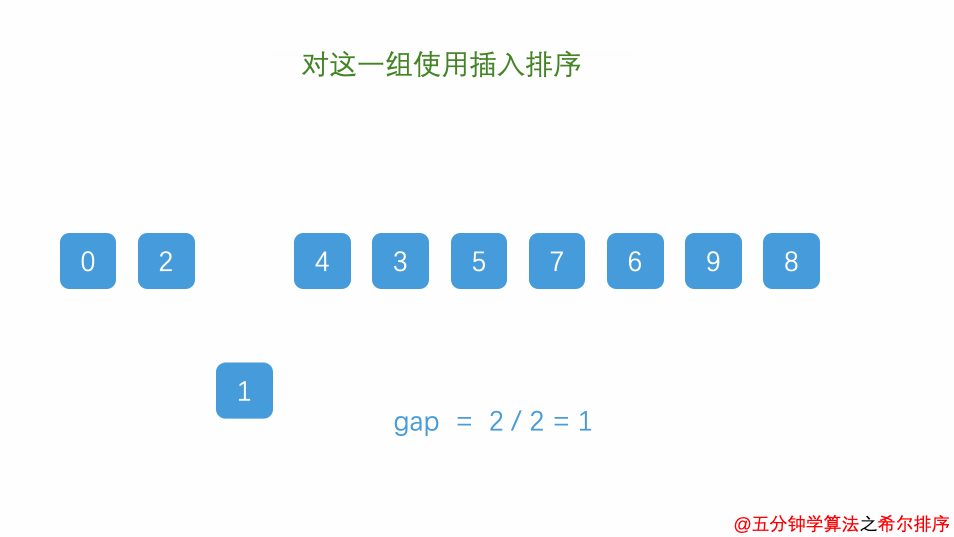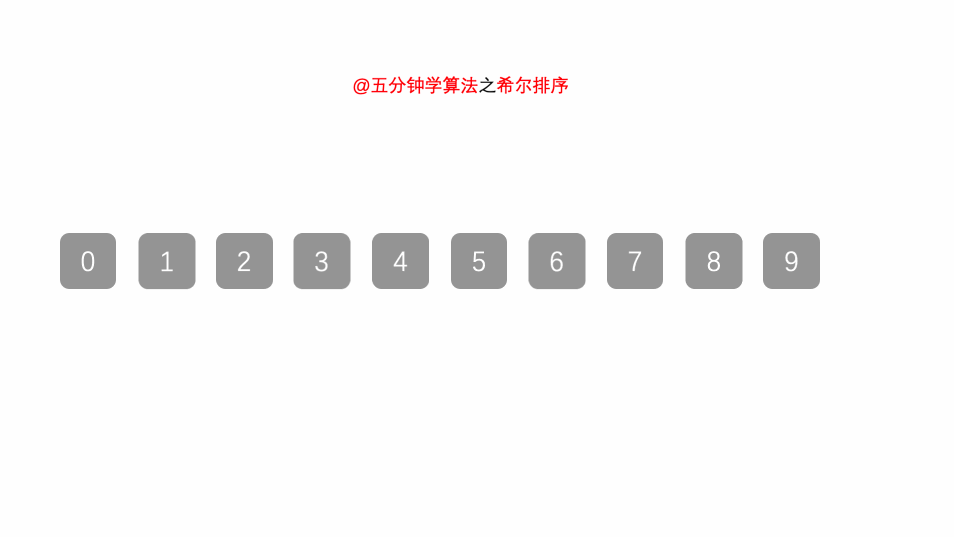
4、希尔排序（Shell Sort）:
class ShellSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;

for (int gap = n / 2; gap > 0; gap /= 2)
{
for (int i = gap; i < n; i++)
{
int temp = arr[i];
int j;
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
{
arr[j] = arr[j - gap];
}
arr[j] = temp;
}
}
}
}
5、归并排序（Merge Sort）:
class MergeSort
{
public static void Sort(int[] arr)
{
if (arr.Length <= 1)
return;

int mid = arr.Length / 2;
int[] leftArr = new int[mid];
int[] rightArr = new int[arr.Length - mid];

for (int i = 0; i < mid; i++)
{
leftArr[i] = arr[i];
}

for (int i = mid; i < arr.Length; i++)
{
rightArr[i - mid] = arr[i];
}

Sort(leftArr);
Sort(rightArr);
Merge(leftArr, rightArr, arr);
}

private static void Merge(int[] leftArr, int[] rightArr, int[] arr)
{
int leftIndex = 0;
int rightIndex = 0;
int current = 0;

while (leftIndex < leftArr.Length && rightIndex < rightArr.Length)
{
if (leftArr[leftIndex] <= rightArr[rightIndex])
{
arr[current] = leftArr[leftIndex];
leftIndex++;
}
else
{
arr[current] = rightArr[rightIndex];
rightIndex++;
}
current++;
}

while (leftIndex < leftArr.Length)
{
arr[current] = leftArr[leftIndex];
leftIndex++;
current++;
}

while (rightIndex < rightArr.Length)
{
arr[current] = rightArr[rightIndex];
rightIndex++;
current++;
}
}
}
6、快速排序（Quick Sort）:
class QuickSort
{
public static void Sort(int[] arr, int low, int high)
{
if (low < high)
{
int pivotIndex = Partition(arr, low, high);
Sort(arr, low, pivotIndex - 1);
Sort(arr, pivotIndex + 1, high);
}
}

private static int Partition(int[] arr, int low, int high)
{
int pivot = arr[high];
int i = low - 1;

for (int j = low; j < high; j++)
{
if (arr[j] < pivot)
{
i++;
Swap(arr, i, j);
}
}

Swap(arr, i + 1, high);
return i + 1;
}

private static void Swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
7、堆排序（Heap Sort）:
class HeapSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;

for (int i = n / 2 - 1; i >= 0; i--)
{
Heapify(arr, n, i);
}

for (int i = n - 1; i > 0; i--)
{
Swap(arr, 0, i);
Heapify(arr, i, 0);
}
}

private static void Heapify(int[] arr, int n, int i)
{
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;

if (left < n && arr[left] > arr[largest])
{
largest = left;
}

if (right < n && arr[right] > arr[largest])
{
largest = right;
}

if (largest != i)
{
Swap(arr, i, largest);
Heapify(arr, n, largest);
}
}

private static void Swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
8、计数排序（Counting Sort）:
class CountingSort
{
public static void Sort(int[] arr)
{
int n = arr.Length;
int[] output = new int[n];

int max = arr[0];
for (int i = 1; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
}

int[] count = new int[max + 1];

for (int i = 0; i < n; i++)
{
count[arr[i]]++;
}

for (int i = 1; i <= max; i++)
{
count[i] += count[i - 1];
}

for (int i = n - 1; i >= 0; i--)
{
output[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}

for (int i = 0; i < n; i++)
{
arr[i] = output[i];
}
}
}

9、桶排序（Bucket Sort）：
using System;
using System.Collections.Generic;

class BucketSort
{
public static void Sort(int[] arr)
{
int minValue = arr[0];
int maxValue = arr[0];

for (int i = 1; i < arr.Length; i++)
{
if (arr[i] < minValue)
minValue = arr[i];
else if (arr[i] > maxValue)
maxValue = arr[i];
}

int bucketSize = maxValue - minValue + 1;
List<int>[] buckets = new List<int>[bucketSize];

for (int i = 0; i < bucketSize; i++)
buckets[i] = new List<int>();

for (int i = 0; i < arr.Length; i++)
buckets[arr[i] - minValue].Add(arr[i]);

int index = 0;
for (int i = 0; i < bucketSize; i++)
{
int[] temp = buckets[i].ToArray();
if (temp.Length > 0)
{
Array.Sort(temp);
for (int j = 0; j < temp.Length; j++)
{
arr[index] = temp[j];
index++;
}
}
}
}

static void Main(string[] args)
{
int[] arr = { 4, 2, 7, 1, 9, 5, 3, 6, 8 };
Console.WriteLine("Before sorting:");
foreach (int element in arr)
Console.Write(element + " ");

Sort(arr);

Console.WriteLine("\n\nAfter sorting:");
foreach (int element in arr)
Console.Write(element + " ");

Console.ReadLine();
}
}
10、基数排序（Radix Sort）：
using System;

class RadixSort
{
public static void Sort(int[] arr)
{
int max = FindMax(arr);

for (int exp = 1; max / exp > 0; exp *= 10)
CountSort(arr, exp);
}

public static void CountSort(int[] arr, int exp)
{
int n = arr.Length;
int[] output = new int[n];
int[] count = new int[10];

for (int i = 0; i < 10; i++)
count[i] = 0;

for (int i = 0; i < n; i++)
count[(arr[i] / exp) % 10]++;

for (int i = 1; i < 10; i++)
count[i] += count[i - 1];

for (int i = n - 1; i >= 0; i--)
{
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}

for (int i = 0; i < n; i++)
arr[i] = output[i];
}

public static int FindMax(int[] arr)
{
int max = arr[0];
for (int i = 1; i < arr.Length; i++)
{
if (arr[i] > max)
max = arr[i];
}
return max;
}

static void Main(string[] args)
{
int[] arr = { 170, 45, 75, 90, 802, 24, 2, 66 };
Console.WriteLine("Before sorting:");
foreach (int element in arr)
Console.Write(element + " ");

Sort(arr);

Console.WriteLine("\n\nAfter sorting:");
foreach (int element in arr)
Console.Write(element + " ");

Console.ReadLine();
}
}

以上代码分别实现了10大算法。请注意，如果需要对其他类型的数据进行排序，需要进行相应的修改。文章来源地址https://www.toymoban.com/news/detail-810754.html

到了这里，关于C# 十大排序算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！