归并思想
在讲解归并排序前,我们先看到一个问题:
对于这样两个有序的数组,如何将它们合并为一个有序的数组?
在此我们处理这个问题的思路就是:开辟一个新的数组,然后分别安置一个指针在左右数组,利用指针遍历数组,每次对比将比较小的那个元素插入到数组的尾部。
像这样:
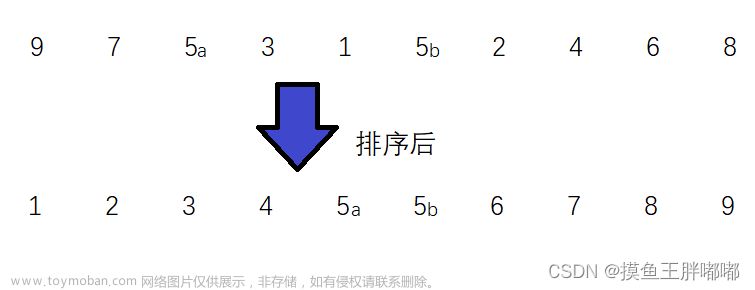
那么我们要如何利用这个思想,让一个无序的数组有序?
比如这个数组:
我们可以这样划分数组:
将其不断往小份划分,划分到最后一段:
对于每一个区域,我们可以认为:左边的一个元素是一个有序数组,右边的一个元素是一个有序数组。然后在对其进行一次归并。
就像这样:
这样我们又得到了8组有序的数组,我们继续归并:
以此类推:
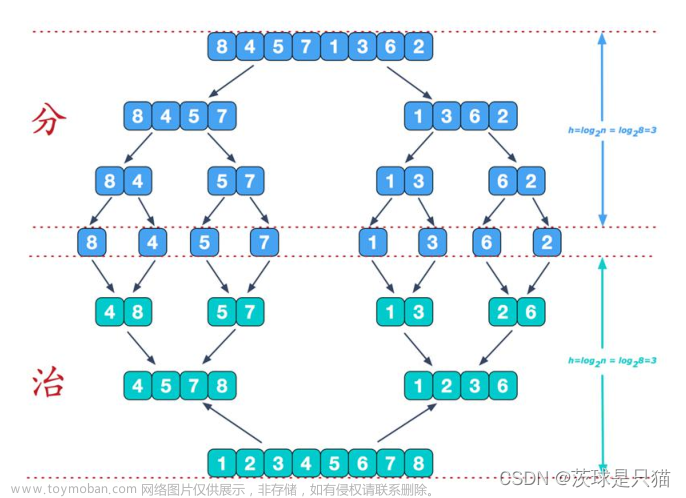
归并排序就是这样一个不断划分子区间,然后进行合并的过程。
递归法
看到不断划分出子区间,毫无疑问这将会是一个递归的过程,而我们将子区间划分到底,再进行处理数据,所以这是同样是一个后序遍历的过程。
在进行合并数组的时候,我们会需要开辟一个新的数组来存放临时的数据。
如果每次合并数组时都额外开辟一段空间,就有点浪费时间了,空间是可以重复利用的,所以我们一开始就要开辟一个和原数组等大的空间。后序进行合并操作都在这个拷贝数组中,当合并完成后,再把数组复制回原数组即可。
那么我们的归并排序一开始要这样写,
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//归并主体
}
void MergeSort(int* a, int n)
{
int*
tmp = (int*)malloc(sizeof(int) * n);//开辟空间
if (tmp == NULL)
{
perror("malloc fali!");
return;
}
_MergeSort(a, 0, n - 1, tmp);//归并主体
free(tmp);
}
_MergeSort函数是归并排序的主体函数,它接受一个待排序的数组a、数组的起始位置begin、数组的结束位置end以及一个临时数组tmp。函数中实现了归并排序的核心部分,即将数组a中的元素从位置begin到位置end进行排序。
MergeSort函数是对_MergeSort函数的封装,它接受一个待排序的数组a和数组的长度n。函数中首先动态分配了一个大小为n的临时数组tmp,用于存放归并时的临时数据,然后调用_MergeSort函数对数组a进行归并排序。排序完成后,释放临时数组tmp的空间。
接下来我们完成归并主体的代码:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;//使拷贝的数组与原数组的位置对应
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
下面是代码的详细步骤解释:
- 首先定义了一个名为
_MergeSort的函数,它接受四个参数:需要排序的数组a、排序区间的起始位置begin和结束位置end,以及一个临时数组tmp。
- 如果
begin大于等于end,说明只有一个元素或者没有元素,直接返回。
- 否则,计算出中间位置
mid,将数组分为左右两个子数组。
- 对左右两个子数组分别调用
_MergeSort函数进行递归排序,直到只剩下一个元素。
- 接下来进行归并操作。定义四个变量
begin1、end1、begin2、end2,分别表示左右子数组的起始和结束位置。
- 定义一个变量
i,用于标记临时数组tmp的位置。
- 开始合并过程,比较左右子数组的元素大小,将较小的元素放入临时数组
tmp中,并递增i和对应的子数组起始位置。
- 如果有一边的子数组已经合并完毕(起始位置大于结束位置),则将另一边的子数组中剩余的元素依次放入临时数组
tmp中。
- 最后,使用
memcpy函数将临时数组tmp中的元素拷贝回原数组a的对应位置。
通过不断递归划分数组为更小的子数组,并借助临时数组tmp进行归并操作,最终完成整个归并排序的过程。
总过程如下:

非递归
其实归并排序也可以使用非递归的方法实现:
我们再次看到这个归并排序的递归图:
可以发现,由于是后序遍历,其实前面在利用递归对数组划分的过程,我们并没有对数组进行任何修改,也就是说我们可以直接把数组划分到每一组只有1个元素,来模拟前半部分的递归。
像这样:
int gap = 1;
for (int i = 0; i < n; i += 2 * gap)
{
//归并数组
}
在这段代码中,变量 gap 初始化为 1,表示每次归并操作对应的子数组的长度。初始时,我们假定待合并的子数组的长度为 1,来模仿前半部分递归划分出来的子数组。i += 2 * gap意味着每次跳过两个子数组,一个gap是一个子数组的长度,2 * gap就是两个子数组的长度。这模仿的是每次合并数组时,被合并的数组区间划分。
那么我们完成了前半部分递归,直接把数组划分为了只有一个元素的小区间,那要如何模仿后半部分?
递归后半部分的工作是,将小区间归并后,形成了一个大区间,接着再把大区间归并,直到这个区间等于原数组长度。
我们想用非递归的思路来模仿后半部分,也就是要实现每次归并区间的增大。
那么每次归并的区间增大多少?
因为每次合并时,是合并了左右两个长度相同的数组,所以归并出的新数组长度应该是2*gap,所以我们每一趟归并,都要把gap翻倍,来模仿区间被合并后增大的效果:
void MergeSortNonR(int* a, int n)
{
int gap = 1;
while (gap < n)//当gap超过n,说明数组合并完毕了
{
for (int i = 0; i < n; i += 2 * gap)
{
//归并主体
}
gap *= 2;//归并完后,下一趟归并的区间翻倍
}
}
那么每次划分出了归并的区间,又要如何划分其内部的两个子数组?
比如这样:
void MergeSortNonR(int* a, int n)
{
int gap = 1;
while (gap < n)//当gap超过n,说明数组合并完毕了
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//对[begin1, end1][begin2, end2]归并
//归并主体
}
gap *= 2;//归并完后,下一趟归并的区间翻倍
}
}
根据这串代码,我们在一个2 * gap范围内,每个gap都是一个子数组,紧接着我们就可以对两个子数组[begin1, end1]和[begin2, end2]归并。
但是这样会产生一个问题,那就是数组的尾部越界了。
我们不能保证每次gap的值都可以被数组整除,所以最后一段gap是有可能会越界的,这要如何控制?
我们一一分析:
对于begin1:
由于
begin1 = i而i < n,所以begin1一定不可能越界。
对于end1 和 begin2:
我们每次归并时,会得到两个已经有序的子区间
[begin1, end1]和[begin2, end2],如果end1和begin2越界,可以理解为[begin2, end2]整个区间都越界了,而[begin1, end1]尚未越界。但是[begin1, end1]是一个已经有序的子区间,所以此时可以不用归并了,直接break,跳过本趟归并。
对于end2:
当
end2越界,相当于是子区间[begin2, end2]有一部分在数组中,有一部分越界。而存在于数组中的那一部分就是[begin2, n - 1],所以此时我们需要将end2的值改为n-1。
让区间[begin1, end1]和[begin2, n - 1]进行归并。
综上我们的非递归大体骨架如下:
void MergeSortNonR(int* a, int n)
{
int gap = 1;//第一趟归并,每个子区间长度为1
while (gap < n)//当gap超过n,说明数组合并完毕了
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//防止越界处理
if (end1 > n || begin2 > n)
{
break;
}
if (end2 > n)
{
end2 = n - 1;
}
//归并主体
}
gap *= 2;//归并完后,下一趟归并的区间翻倍
}
}
而归并主体部分已经讲解过,就是利用两个指针,每次取出最小的元素插入到新的数组中,再将新数组拷贝回去。文章来源:https://www.toymoban.com/news/detail-810770.html
总代码如下:文章来源地址https://www.toymoban.com/news/detail-810770.html
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fali!");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 > n || begin2 > n)
{
break;
}
if (end2 > n)
{
end2 = n - 1;
}
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap *= 2;
}
free(tmp);
}
到了这里,关于数据结构与算法:归并排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![[数据结构 -- 手撕排序算法第七篇] 递归实现归并排序](https://imgs.yssmx.com/Uploads/2024/02/573259-1.png)