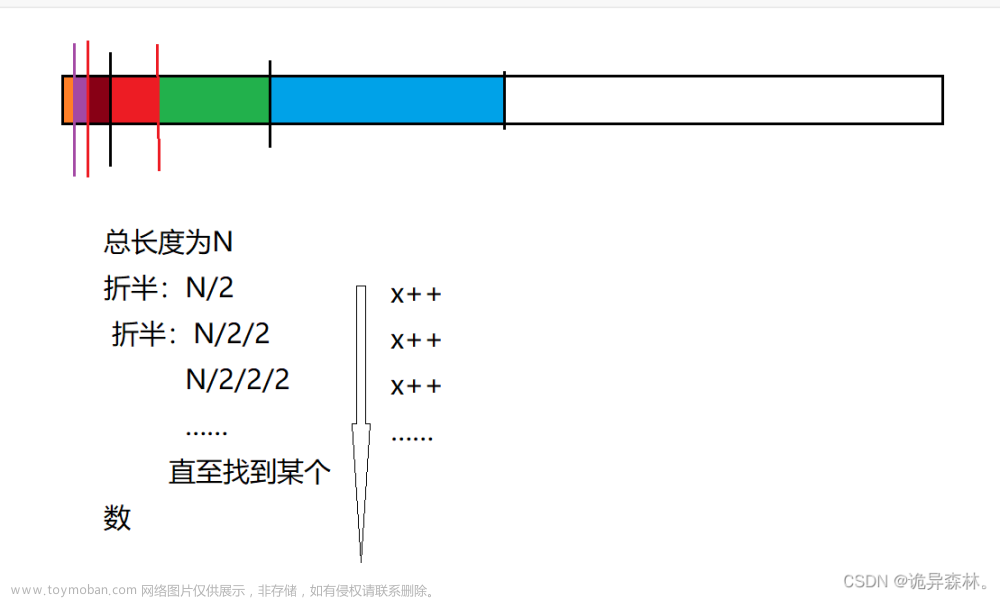
归并排序是证明计算复杂度领域的一个重要结论的基础,而计算复杂性能够帮助我们理解排序自身固有的难易程度。计算复杂性在算法设计中扮演着非常重要的角色。
研究复杂度的第一步是建立一个计算模型。一般来说,研究者会尽量寻找一个和问题相关的最简单的模型。对排序来说,研究对象是基于比较的算法,它们对数组元素的操作方式是由主键的比较决定的。一个基于比较的算法在两次比较之间可能会进行任意规模的计算,但它只能通过主键之间的比较得到某个主键的信息。
没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较将长度为N的数组排序。
归并排序是一种渐进最优的基于比较排序的算法。
需要强调的是,和计算模型一样,我们需要精确地定义最优算法,在适用的情况下,关键在于计算复杂度会影响优秀软件的开发。
归并排序的最优性并不是结束,因为还有些其他情况:
1、归并排序的空间复杂度不是最优的
2、在实践中不一定会遇到最坏情况
3、除了比较,算法的其他操作也可能很重要,比如访问数组文章来源:https://www.toymoban.com/news/detail-811055.html
4、不进行比较也能将某些数据排序。文章来源地址https://www.toymoban.com/news/detail-811055.html
到了这里,关于【排序算法】排序算法的复杂度的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!