[高精度加法与动态规划混合] 数楼梯-Toy模板网

这篇具有很好参考价值的文章主要介绍了[高精度加法与动态规划混合] 数楼梯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数楼梯

题目描述

楼梯有 $N$ 阶，上楼可以一步上一阶，也可以一步上二阶。

编一个程序，计算共有多少种不同的走法。

输入格式

一个数字，楼梯数。

输出格式

输出走的方式总数。

样例 #1

样例输入 #1

样例输出 #1

6276302800488957086035253108349684055478528702736457439025824448927937256811663264475883711527806250329984690249846819800648580083040107584710332687596562185073640422286799239932615797105974710857095487342820351307477141875012176874307156016229965832589137779724973854362777629878229505500260477136108363709090010421536915488632339240756987974122598603591920306874926755600361865354330444681915154695741851960071089944015319300128574107662757054790648152751366475529121877212785489665101733755898580317984402963873738187000120737824193162011399200547424034440836239726275765901190914513013217132050988064832024783370583789324109052449717186857327239783000020791777804503930439875068662687670678802914269784817022567088069496231111407908953313902398529655056082228598715882365779469902465675715699187225655878240668599547496218159297881601061923195562143932693324644219266564617042934227893371179832389642895285401263875342640468017378925921483580111278055044254198382265567395946431803304304326865077742925818757370691726168228648841319231470626

提示

对于 $60\%$ 的数据， $\leq 50$ ；
对于 $100\%$ 的数据， $\le N \leq 5000$ 。

解题分析

注意到本题数据十分十分的大，即使是long long int都没办法存储，考虑将高精度加法与之混合。
对于这个数楼梯的问题，其实是很经典的动态规划问题，到达第n个台阶的方法数会等于到达n-1个台阶的方法数加上到达n-2个台阶的方法数。
即

f[n]=f[n-1]+f[n-2]

十分清晰，接下来就是考虑利用高精度加法进行计算即可。

主要使用了动态规划和大数加法两种算法去解决这个上楼梯的问题。以下是详细的解析：

动态规划算法：

动态规划是这里的主要算法，用于解决上楼梯的问题。对于 n 阶楼梯，设 f(n) 为走到第 n 阶楼的方法数量，那么 f(n) 可以分解为：

从第 n-1 阶上一步走到第 n 阶，这种方法有 f(n-1) 种
从第 n-2 阶上两步走到第 n 阶，这种方法有 f(n-2) 种

所以，f(n) = f(n-1) + f(n-2)。这就是动态规划的状态转移方程。

我们知道，当 n=1 或 n=0 时，f(n) 都等于 1 (只有一种上法)，所以这是递归的基准条件。

大数加法算法：

由于题目中 n 可能最大为 5000，通过上面的递推关系不难看出，结果可能会超过程序中基本数据类型的范围，这时我们可以使用大数加法来储存和计算具有大量数字的整数。

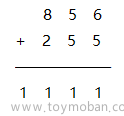
具体来说，大数加法先将两个大数字符串逆序并转化为整数，然后从低位到高位依次相加。如果某位相加的结果大于等于10，则需要进位。这在代码中体现为：

num3[i]=num1[i]+num2[i];——当前位的加法
num1[i+1]+=num3[i]/10; ——向高位的进位处理
num3[i]%=10; ——保留当前位的余数

最后，将计算出的结果数组 num3 逆序，并转化为字符串返回。文章来源地址https://www.toymoban.com/news/detail-811348.html

具体的代码实现：

设置大数动态规划数组 num dp[5005];
复制初始值到第0阶和第1阶，表示没有楼梯和有一阶楼梯时的走法数目都是1.
遍历动态规划数组 dp，用 add(dp[i-1].number, dp[i-2].number) 计算 dp[i]。
最后输出 dp[N].number，这就是走上N阶楼梯的全部方法数。

代码实现

#include <iostream>
#include <cstring>
using namespace std;
struct num{
	char number[5005];
};

num dp[5005];
int num1[5005],num2[5005],num3[5005];
char result[5005];

char *add(char *number1,char *number2){
	int len1=strlen(number1),len2=strlen(number2);
	int len=max(len1,len2);
	memset(num1,0,sizeof(num1));
	memset(num2,0,sizeof(num2));
	memset(num3,0,sizeof(num3));
	memset(result,0,sizeof(result));
	for(int i=0,j=len1-1;i<len1;i++,j--){
		num1[i]=number1[j]-'0';
	}
	for(int i=0,j=len2-1;i<len2;i++,j--){
		num2[i]=number2[j]-'0';
	}
	for(int i=0;i<=len;i++){
		num3[i]=num1[i]+num2[i];
		num1[i+1]+=num3[i]/10;
		num3[i]%=10;
	}
	int k=0,l=0;
	for(l=5004;l>=0;l--){
		if(num3[l]){
			break;
		}
	}
	for(;l>=0;l--){
		result[k++]=num3[l]+'0';
	}
	result[k]='\0';
	return result;
}

int main(){
	int N; cin>>N;
	strcpy(dp[0].number,"1");
	strcpy(dp[1].number,"1");
	for(int i=2;i<=N;i++){
		strncpy(dp[i].number,add(dp[i-1].number,dp[i-2].number),5000);
	}
	printf("%s",dp[N].number);
	return 0;
}