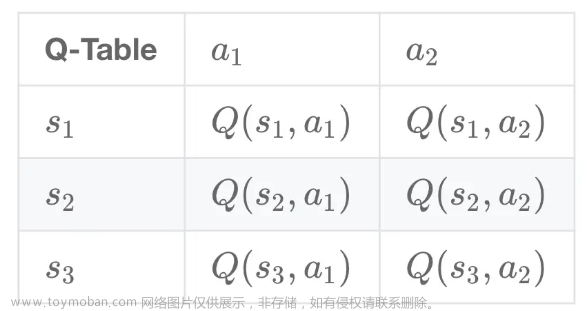
值函数可以分为状态价值函数和动作价值函数,分别适用于哪些强化学习问题


二、基于动态规划的算法



2.1 策略迭代算法


示例:


(改进的) 策略迭代

代码
首先定义了一些参数,如奖励、折扣因子、最大误差等,然后初始化了一个网格世界的环境,包括状态、动作、价值函数和策略。接着,它定义了一些函数,用于打印网格世界的状态或策略、计算状态的期望价值函数、对策略进行评估和改进等。最后,它使用了策略迭代的算法,不断地更新策略和价值函数,直到找到最优的策略,并打印出初始的随机策略和最终的最优策略。
import random # 导入随机模块,用于生成随机数
# Arguments
REWARD = -0.01 # 定义非终止状态的常数奖励,这里是负数,表示每走一步都有一定的代价
DISCOUNT = 0.99 # 定义折扣因子,表示未来奖励的衰减程度,越接近1表示越重视长期奖励
MAX_ERROR = 10**(-3) # 定义最大误差,表示当状态的价值函数的变化小于这个值时,认为收敛到稳定值
# Set up the initial environment
NUM_ACTIONS = 4 # 定义动作的数量,这里是4个,分别是上下左右四个方向的移动。policy里的0~3. # Down, Left, Up, Right
ACTIONS = [(1, 0), (0, -1), (-1, 0), (0, 1)] # 定义动作的具体效果,表示每个动作对行和列的坐标的影响,例如(1, 0)表示向下移动一格,行坐标加1,列坐标不变
NUM_ROW = 3 # 定义网格世界的行数
NUM_COL = 4 # 定义网格世界的列数
U = [[0, 0, 0, 1], [0, 0, 0, -1], [0, 0, 0, 0], [0, 0, 0, 0]] # 定义每个状态的初始价值函数,这里只有两个终止状态有正负1的奖励,其他状态都是0
policy = [[random.randint(0, 3) for j in range(NUM_COL)] for i in range(NUM_ROW)] # 随机生成一个初始策略,每个状态随机选择一个动作,用0到3的整数表示
# Visualization
def printEnvironment(arr, policy=False): # 定义一个函数,用于打印网格世界的状态或策略
res = "" # 初始化一个空字符串,用于存储打印的结果
for r in range(NUM_ROW): # 遍历每一行
res += "|" # 在每一行的开头加上一个竖线符号
for c in range(NUM_COL): # 遍历每一列
if r == c == 1: # 如果是中间的墙壁状态,用WALL表示
val = "WALL"
elif r <= 1 and c == 3: # 如果是右上角或右下角的终止状态,用+1或-1表示
val = "+1" if r == 0 else "-1"
else: # 如果是其他状态,用动作的方向表示,例如Down, Left, Up, Right
val = ["Down", "Left", "Up", "Right"][arr[r][c]]
res += " " + val[:5].ljust(5) + " |" # 格式化输出,每个状态占6个字符,不足的用空格补齐,然后加上一个竖线符号
res += "\n" # 每一行结束后换行
print(res) # 打印结果
# Get the utility of the state reached by performing the given action from the given state
def getU(U, r, c, action): # 定义一个函数,用于获取从给定的状态执行给定的动作后到达的状态的价值函数
dr, dc = ACTIONS[action] # 根据动作的编号,获取动作对行和列坐标的影响
newR, newC = r+dr, c+dc # 计算新的行和列坐标
if newR < 0 or newC < 0 or newR >= NUM_ROW or newC >= NUM_COL or (newR == newC == 1): # 如果新的坐标超出了网格的范围,或者碰到了墙壁,表示无效的移动
return U[r][c] # 返回原来的状态的价值函数
else: # 否则
return U[newR][newC] # 返回新的状态的价值函数
# Calculate the utility of a state given an action
def calculateU(U, r, c, action): # 定义一个函数,用于计算给定状态和动作的期望价值函数
u = REWARD # 初始化价值函数为常数奖励
# 状态转移概率 0.1左偏 0.8前行 0.1右偏
u += 0.1 * DISCOUNT * getU(U, r, c, (action-1)%4) # 加上向左偏转10%的概率的折扣后的价值函数
u += 0.8 * DISCOUNT * getU(U, r, c, action) # 加上按照策略执行80%的概率的折扣后的价值函数
u += 0.1 * DISCOUNT * getU(U, r, c, (action+1)%4) # 加上向右偏转10%的概率的折扣后的价值函数
return u # 返回计算的结果
# Perform some simplified value iteration steps to get an approximation of the utilities
def policyEvaluation(policy, U): # 定义一个函数,用于对给定的策略进行策略评估,即计算策略对应的价值函数
while True: # 不断循环,直到收敛
nextU = [[0, 0, 0, 1], [0, 0, 0, -1], [0, 0, 0, 0], [0, 0, 0, 0]] # 初始化下一轮的价值函数,终止状态的价值函数不变,其他状态为0
error = 0 # 初始化最大误差为0。 相邻两次迭代的价值函数的差值
for r in range(NUM_ROW): # 遍历每一行
for c in range(NUM_COL): # 遍历每一列
if (r <= 1 and c == 3) or (r == c == 1): # 如果是终止状态或墙壁状态,跳过
continue
nextU[r][c] = calculateU(U, r, c, policy[r][c])# 更新状态价值函数 # 根据当前的价值函数和策略,计算下一轮的价值函数,这里使用了简化的贝尔曼更新公式
error = max(error, abs(nextU[r][c]-U[r][c])) # 更新状态价值函数最大差值
U = nextU # 用下一轮的价值函数替换当前的价值函数
if error < MAX_ERROR * (1-DISCOUNT) / DISCOUNT: # 如果最大误差小于一个阈值(MAX_ERROR * (1-DISCOUNT) / DISCOUNT 人工设定的),表示收敛
break # 退出循环
return U # 返回收敛后的价值函数
def policyIteration(policy, U): # 定义一个函数,用于对给定的策略进行策略迭代,即不断地进行策略评估和策略改进,直到找到最优策略
print("During the policy iteration:\n") # 打印提示信息
while True: # 不断循环,直到收敛
U = policyEvaluation(policy, U) # 对当前的策略进行策略评估,得到价值函数
unchanged = True # 初始化一个标志,表示策略是否发生了改变
for r in range(NUM_ROW): # 遍历每一行
for c in range(NUM_COL): # 遍历每一列
if (r <= 1 and c == 3) or (r == c == 1): # 如果是终止状态或墙壁状态,跳过
continue
maxAction, maxU = None, -float("inf") # 初始化最大价值函数和对应的动作为无穷小和空值
for action in range(NUM_ACTIONS): # 遍历所有可能的动作
u = calculateU(U, r, c, action) # 计算当前状态和动作的期望价值函数
if u > maxU: # 如果当前的价值函数大于最大价值函数
maxAction, maxU = action, u # 更新最大价值函数和对应的动作
if maxU > calculateU(U, r, c, policy[r][c]): # 如果最大价值函数大于当前策略(所确定动作)对应的价值函数
policy[r][c] = maxAction # 更新策略为最大价值函数对应的动作
unchanged = False # 标记策略发生了改变
if unchanged: # 如果策略没有发生改变,表示已经找到了最优策略
break # 退出循环
printEnvironment(policy) # 打印当前的策略
return policy # 返回最优策略
# Print the initial environment
print("The initial random policy is:\n") # 打印提示信息
printEnvironment(policy) # 打印初始的随机策略
# Policy iteration
policy = policyIteration(policy, U) # 调用策略迭代函数,得到最优策略
# Print the optimal policy
print("The optimal policy is:\n") # 打印提示信息
printEnvironment(policy) # 打印最优策略输出结果:
The initial random policy is:
| Up | Right | Right | +1 |
| Down | WALL | Left | -1 |
| Left | Up | Right | Left |
During the policy iteration:
| Up | Right | Right | +1 |
| Up | WALL | Up | -1 |
| Right | Right | Up | Down |
| Right | Right | Right | +1 |
| Up | WALL | Left | -1 |
| Up | Right | Up | Down |
| Right | Right | Right | +1 |
| Up | WALL | Left | -1 |
| Up | Left | Up | Down |
| Right | Right | Right | +1 |
| Up | WALL | Left | -1 |
| Up | Left | Left | Down |
The optimal policy is:
| Right | Right | Right | +1 |
| Up | WALL | Left | -1 |
| Up | Left | Left | Down |2.2 价值迭代算法


示例-价值迭代算法

代码
首先定义了一些参数,如奖励、折扣因子、最大误差等,然后初始化了一个网格世界的环境,包括状态、动作、价值函数。接着,它定义了一些函数,用于打印网格世界的状态或策略、计算状态的期望价值函数、对价值函数进行价值迭代等。最后,它使用了价值迭代的算法,不断地更新价值函数,直到收敛,并根据价值函数获取最优的策略,并打印出初始的价值函数和最终的最优策略。
REWARD = -0.01 # 定义非终止状态的常数奖励,这里是负数,表示每走一步都有一定的代价
DISCOUNT = 0.99 # 定义折扣因子,表示未来奖励的衰减程度,越接近1表示越重视长期奖励
MAX_ERROR = 10**(-3) # 定义最大误差,表示当状态的价值函数的变化小于这个值时,认为收敛到稳定值
# Set up the initial environment
NUM_ACTIONS = 4 # 定义动作的数量,这里是4个,分别是上下左右四个方向的移动
ACTIONS = [(1, 0), (0, -1), (-1, 0), (0, 1)] # 定义动作的具体效果,表示每个动作对行和列的坐标的影响,例如(1, 0)表示向下移动一格,行坐标加1,列坐标不变
NUM_ROW = 3 # 定义网格世界的行数
NUM_COL = 4 # 定义网格世界的列数
U = [[0, 0, 0, 1], [0, 0, 0, -1], [0, 0, 0, 0], [0, 0, 0, 0]] # 定义每个状态的初始价值函数,这里只有两个终止状态有正负1的奖励,其他状态都是0
# Visualization
def printEnvironment(arr, policy=False): # 定义一个函数,用于打印网格世界的状态或策略
res = "" # 初始化一个空字符串,用于存储打印的结果
for r in range(NUM_ROW): # 遍历每一行
res += "|" # 在每一行的开头加上一个竖线符号
for c in range(NUM_COL): # 遍历每一列
if r == c == 1: # 如果是中间的墙壁状态,用WALL表示
val = "WALL"
elif r <= 1 and c == 3: # 如果是右上角或右下角的终止状态,用+1或-1表示
val = "+1" if r == 0 else "-1"
else: # 如果是其他状态
if policy: # 如果是打印策略,用动作的方向表示,例如Down, Left, Up, Right
val = ["Down", "Left", "Up", "Right"][arr[r][c]]
else: # 如果是打印价值函数,用状态的价值表示,转换为字符串
val = str(arr[r][c])
res += " " + val[:5].ljust(5) + " |" # 格式化输出,每个状态占6个字符,不足的用空格补齐,然后加上一个竖线符号
res += "\n" # 每一行结束后换行
print(res) # 打印结果
# Get the utility of the state reached by performing the given action from the given state
def getU(U, r, c, action): # 定义一个函数,用于获取从给定的状态执行给定的动作后到达的状态的价值函数
dr, dc = ACTIONS[action] # 根据动作的编号,获取动作对行和列坐标的影响
newR, newC = r+dr, c+dc # 计算新的行和列坐标
if newR < 0 or newC < 0 or newR >= NUM_ROW or newC >= NUM_COL or (newR == newC == 1): # 如果新的坐标超出了网格的范围,或者碰到了墙壁,表示无效的移动
return U[r][c] # 返回原来的状态的价值函数
else: # 否则
return U[newR][newC] # 返回新的状态的价值函数
# Calculate the utility of a state given an action
def calculateU(U, r, c, action): # 定义一个函数,用于计算给定状态和动作的期望价值函数
u = REWARD # 初始化价值函数为常数奖励
u += 0.1 * DISCOUNT * getU(U, r, c, (action-1)%4) # 加上向左偏转10%的概率的折扣后的价值函数
u += 0.8 * DISCOUNT * getU(U, r, c, action) # 加上按照策略执行80%的概率的折扣后的价值函数
u += 0.1 * DISCOUNT * getU(U, r, c, (action+1)%4) # 加上向右偏转10%的概率的折扣后的价值函数
return u # 返回计算的结果
#价值迭代利用贝尔曼最优性方程来鞥新状态价值函数,每次选择在当前状态下达到最优值的动作
def valueIteration(U): # 定义一个函数,用于对价值函数进行价值迭代,即不断地更新价值函数,直到收敛
print("During the value iteration:\n") # 打印提示信息
while True: # 不断循环,直到收敛
nextU = [[0, 0, 0, 1], [0, 0, 0, -1], [0, 0, 0, 0], [0, 0, 0, 0]] # 初始化下一轮的价值函数,终止状态的价值函数不变,其他状态为0
error = 0 # 初始化最大误差为0
for r in range(NUM_ROW): # 遍历每一行
for c in range(NUM_COL): # 遍历每一列
if (r <= 1 and c == 3) or (r == c == 1): # 如果是终止状态或墙壁状态,跳过
continue
nextU[r][c] = max([calculateU(U, r, c, action) for action in range(NUM_ACTIONS)]) # 根据当前的价值函数和所有可能的动作,计算下一轮的价值函数,这里使用了贝尔曼最优化更新公式
error = max(error, abs(nextU[r][c]-U[r][c])) # 更新最大误差
U = nextU # 用下一轮的价值函数替换当前的价值函数
printEnvironment(U) # 打印当前的价值函数
if error < MAX_ERROR * (1-DISCOUNT) / DISCOUNT: # 如果最大误差小于一个阈值,表示收敛
break # 退出循环
return U # 返回收敛后的价值函数
# Get the optimal policy from U
def getOptimalPolicy(U): # 定义一个函数,用于根据价值函数获取最优策略,即每个状态选择使得价值函数最大的动作
policy = [[-1, -1, -1, -1] for i in range(NUM_ROW)] # 初始化策略为-1,表示无效的动作
for r in range(NUM_ROW): # 遍历每一行
for c in range(NUM_COL): # 遍历每一列
if (r <= 1 and c == 3) or (r == c == 1): # 如果是终止状态或墙壁状态,跳过
continue
# Choose the action that maximizes the utility
maxAction, maxU = None, -float("inf") # 初始化最大价值函数和对应的动作为无穷小和空值
for action in range(NUM_ACTIONS): # 遍历所有可能的动作
u = calculateU(U, r, c, action) # 计算当前状态和动作的期望价值函数
if u > maxU: # 如果当前的价值函数大于最大价值函数
maxAction, maxU = action, u # 更新最大价值函数和对应的动作
policy[r][c] = maxAction # 将当前状态的策略更新为最大价值函数对应的动作
return policy # 返回最优策略
# Print the initial environment
print("The initial U is:\n") # 打印提示信息
printEnvironment(U) # 打印初始的价值函数
# Value iteration
U = valueIteration(U) # 调用价值迭代函数,得到收敛后的价值函数
# Get the optimal policy from U and print it
policy = getOptimalPolicy(U) # 调用获取最优策略的函数,得到最优策略
print("The optimal policy is:\n") # 打印提示信息
printEnvironment(policy, True) # 打印最优策略输出结果:
The initial U is:
| 0 | 0 | 0 | +1 |
| 0 | WALL | 0 | -1 |
| 0 | 0 | 0 | 0 |
During the value iteration:
| -0.01 | -0.01 | 0.782 | +1 |
| -0.01 | WALL | -0.01 | -1 |
| -0.01 | -0.01 | -0.01 | -0.01 |
| -0.01 | 0.607 | 0.858 | +1 |
| -0.01 | WALL | 0.509 | -1 |
| -0.01 | -0.01 | -0.01 | -0.01 |
| 0.467 | 0.790 | 0.917 | +1 |
| -0.02 | WALL | 0.621 | -1 |
| -0.02 | -0.02 | 0.389 | -0.02 |
| 0.659 | 0.873 | 0.934 | +1 |
| 0.354 | WALL | 0.679 | -1 |
| -0.03 | 0.292 | 0.476 | 0.196 |
| 0.781 | 0.902 | 0.941 | +1 |
| 0.582 | WALL | 0.698 | -1 |
| 0.295 | 0.425 | 0.576 | 0.287 |
| 0.840 | 0.914 | 0.944 | +1 |
| 0.724 | WALL | 0.705 | -1 |
| 0.522 | 0.530 | 0.613 | 0.375 |
| 0.869 | 0.919 | 0.945 | +1 |
| 0.798 | WALL | 0.708 | -1 |
| 0.667 | 0.580 | 0.638 | 0.414 |
| 0.883 | 0.920 | 0.945 | +1 |
| 0.836 | WALL | 0.709 | -1 |
| 0.746 | 0.634 | 0.649 | 0.437 |
| 0.889 | 0.921 | 0.945 | +1 |
| 0.854 | WALL | 0.710 | -1 |
| 0.789 | 0.706 | 0.658 | 0.449 |
| 0.892 | 0.921 | 0.945 | +1 |
| 0.863 | WALL | 0.711 | -1 |
| 0.815 | 0.754 | 0.685 | 0.456 |
| 0.893 | 0.921 | 0.946 | +1 |
| 0.867 | WALL | 0.714 | -1 |
| 0.829 | 0.785 | 0.726 | 0.478 |
| 0.894 | 0.921 | 0.946 | +1 |
| 0.869 | WALL | 0.721 | -1 |
| 0.837 | 0.802 | 0.754 | 0.513 |
| 0.894 | 0.922 | 0.947 | +1 |
| 0.870 | WALL | 0.730 | -1 |
| 0.841 | 0.811 | 0.771 | 0.539 |
| 0.895 | 0.922 | 0.948 | +1 |
| 0.870 | WALL | 0.738 | -1 |
| 0.843 | 0.816 | 0.781 | 0.555 |
| 0.895 | 0.923 | 0.948 | +1 |
| 0.871 | WALL | 0.746 | -1 |
| 0.844 | 0.819 | 0.787 | 0.565 |
| 0.896 | 0.924 | 0.949 | +1 |
| 0.871 | WALL | 0.752 | -1 |
| 0.844 | 0.820 | 0.790 | 0.571 |
| 0.897 | 0.925 | 0.950 | +1 |
| 0.872 | WALL | 0.758 | -1 |
| 0.845 | 0.821 | 0.792 | 0.577 |
| 0.898 | 0.926 | 0.951 | +1 |
| 0.873 | WALL | 0.763 | -1 |
| 0.846 | 0.822 | 0.794 | 0.583 |
| 0.898 | 0.926 | 0.951 | +1 |
| 0.874 | WALL | 0.767 | -1 |
| 0.846 | 0.822 | 0.795 | 0.588 |
| 0.899 | 0.927 | 0.952 | +1 |
| 0.874 | WALL | 0.770 | -1 |
| 0.847 | 0.823 | 0.796 | 0.592 |
| 0.900 | 0.927 | 0.952 | +1 |
| 0.875 | WALL | 0.773 | -1 |
| 0.848 | 0.824 | 0.797 | 0.596 |
| 0.900 | 0.928 | 0.952 | +1 |
| 0.876 | WALL | 0.775 | -1 |
| 0.849 | 0.825 | 0.798 | 0.600 |
| 0.900 | 0.928 | 0.953 | +1 |
| 0.876 | WALL | 0.777 | -1 |
| 0.849 | 0.825 | 0.799 | 0.604 |
| 0.901 | 0.928 | 0.953 | +1 |
| 0.877 | WALL | 0.779 | -1 |
| 0.850 | 0.826 | 0.800 | 0.607 |
| 0.901 | 0.928 | 0.953 | +1 |
| 0.877 | WALL | 0.781 | -1 |
| 0.850 | 0.827 | 0.800 | 0.610 |
| 0.901 | 0.929 | 0.953 | +1 |
| 0.877 | WALL | 0.782 | -1 |
| 0.851 | 0.827 | 0.801 | 0.613 |
| 0.902 | 0.929 | 0.953 | +1 |
| 0.878 | WALL | 0.783 | -1 |
| 0.851 | 0.827 | 0.802 | 0.615 |
| 0.902 | 0.929 | 0.953 | +1 |
| 0.878 | WALL | 0.784 | -1 |
| 0.851 | 0.828 | 0.802 | 0.618 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.878 | WALL | 0.785 | -1 |
| 0.851 | 0.828 | 0.803 | 0.620 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.878 | WALL | 0.785 | -1 |
| 0.852 | 0.828 | 0.803 | 0.622 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.878 | WALL | 0.786 | -1 |
| 0.852 | 0.828 | 0.803 | 0.623 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.878 | WALL | 0.786 | -1 |
| 0.852 | 0.829 | 0.803 | 0.625 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.879 | WALL | 0.787 | -1 |
| 0.852 | 0.829 | 0.804 | 0.626 |
| 0.902 | 0.929 | 0.954 | +1 |
| 0.879 | WALL | 0.787 | -1 |
| 0.852 | 0.829 | 0.804 | 0.628 |
| 0.902 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.787 | -1 |
| 0.852 | 0.829 | 0.804 | 0.629 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.852 | 0.829 | 0.804 | 0.630 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.852 | 0.829 | 0.804 | 0.631 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.852 | 0.829 | 0.804 | 0.632 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.853 | 0.829 | 0.804 | 0.632 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.853 | 0.829 | 0.805 | 0.633 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.788 | -1 |
| 0.853 | 0.829 | 0.805 | 0.634 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.829 | 0.805 | 0.634 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.635 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.635 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.636 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.636 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.636 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.637 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.637 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.637 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.637 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.638 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
| 0.903 | 0.930 | 0.954 | +1 |
| 0.879 | WALL | 0.789 | -1 |
| 0.853 | 0.830 | 0.805 | 0.639 |
The optimal policy is:
| Right | Right | Right | +1 |
| Up | WALL | Left | -1 |
| Up | Left | Left | Down |2.3 价值迭代算法与策略迭代算法对比
策略迭代算法和价值迭代算法都依赖于环境的模型,需要知道状态转移概率和回报函数,因此被称为有模型的强化学习算法。

 文章来源:https://www.toymoban.com/news/detail-811372.html
文章来源:https://www.toymoban.com/news/detail-811372.html
The End文章来源地址https://www.toymoban.com/news/detail-811372.html
到了这里,关于【机器学习】强化学习(二)基于动态规划的算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!