1. Toy模板网首页
  2. > Toy博客

稀疏矩阵的三元组表示----（算法详解）

9月前 作者：gobeyye 分类：Toy博客 阅读(37) 违法举报

这篇具有很好参考价值的文章主要介绍了稀疏矩阵的三元组表示----（算法详解）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

基本算法包括：（解释都在代码里）

1.创建

2.对三元组元素赋值

3.将三元组元素赋值给变量

4.输出三元组

5.转置（附加的有兴趣可以看看）

稀疏矩阵的概念：矩阵的非零元素相较零元素非常小时，这个矩阵就叫稀疏矩阵。

稀疏矩阵可以用三元组表示和十字链表表示

本文章介绍三元组表示

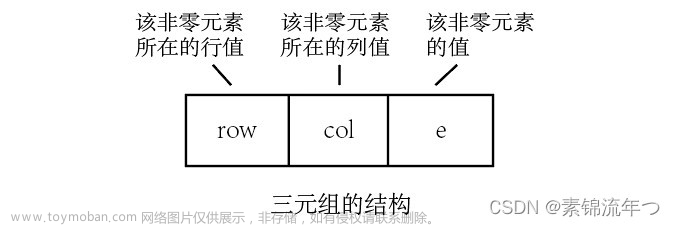
稀疏矩阵的三元组表示。

三元组表示就是，用三个变量来存储非零元素的信息。

三元组线性表按顺序存储结构存储。

三元组顺序表的数据类型声明如下：

#include <stdio.h>
#define M 6
#define N 7
#define MaxSize  100         //矩阵中非零元素最多个数
typedef int ElemType;
typedef struct
{
	int r;					//行号
	int c;					//列号
	ElemType d;				//元素值
} TupNode;					//三元组定义
typedef struct 
{	
	int rows;				//行数
	int cols;				//列数
	int nums;				//非零元素个数
	TupNode data[MaxSize];
} TSMatrix;					//三元组顺序表

基本算法包括：（解释都在代码里）

1.创建

2.对三元组元素赋值

3.将三元组元素赋值给变量

4.输出三元组

5.转置（附加的有兴趣可以看看）

1.创建：

void CreatMat(TSMatrix &t,ElemType A[M][N])  //从一个二维稀疏矩阵创建其三元组表示
{
	int i,j;
	t.rows=M;t.cols=N;t.nums=0;
	for (i=0;i<M;i++)
	{
		for (j=0;j<N;j++) 
			if (A[i][j]!=0) 	//只存储非零元素
			{
				t.data[t.nums].r=i;t.data[t.nums].c=j;
				t.data[t.nums].d=A[i][j];t.nums++;
			}
	}
}

2.对三元组元素赋值

先找行后找列

bool Value(TSMatrix &t,ElemType x,int i,int j)  //三元组元素赋值
{
	int k=0,k1;
	if (i>=t.rows || j>=t.cols)
		return false;				//失败时返回false
	while (k<t.nums && i>t.data[k].r) k++;					//查找行
	while (k<t.nums && i==t.data[k].r && j>t.data[k].c) k++;//查找列
	if (t.data[k].r==i && t.data[k].c==j)	//存在这样的元素
		t.data[k].d=x;
	else									//不存在这样的元素时插入一个元素
	{	
		for (k1=t.nums-1;k1>=k;k1--)
		{
			t.data[k1+1].r=t.data[k1].r;
			t.data[k1+1].c=t.data[k1].c;
			t.data[k1+1].d=t.data[k1].d;
		}
		t.data[k].r=i;t.data[k].c=j;t.data[k].d=x;
		t.nums++;
	}
	return true;						//成功时返回true
}

3.将三元组元素赋值给变量

bool Assign(TSMatrix t,ElemType &x,int i,int j)  //将指定位置的元素值赋给变量
{
	int k=0;
	if (i>=t.rows || j>=t.cols)
		return false;			//失败时返回false
	while (k<t.nums && i>t.data[k].r) k++;					//查找行
	while (k<t.nums && i==t.data[k].r && j>t.data[k].c) k++;//查找列
	if (t.data[k].r==i && t.data[k].c==j)
		x=t.data[k].d;
	else
		x=0;				//在三元组中没有找到表示是零元素
	return true;			//成功时返回true
}

4.输出三元组

void DispMat(TSMatrix t)		//输出三元组
{
	int i;
	if (t.nums<=0)			//没有非零元素时返回
		return;
	printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums);
	printf("\t------------------\n");
	for (i=0;i<t.nums;i++)
		printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d);
}

5.转置（附加的有兴趣可以看看）

void TranTat(TSMatrix t,TSMatrix &tb)		//矩阵转置
{
	int p,q=0,v;					//q为tb.data的下标
	tb.rows=t.cols;tb.cols=t.rows;tb.nums=t.nums;
	if (t.nums!=0)					//当存在非零元素时执行转置
	{
		for (v=0;v<t.cols;v++)		//tb.data[q]中的记录以c域的次序排列
			for (p=0;p<t.nums;p++)	//p为t.data的下标
				if (t.data[p].c==v)
				{
					tb.data[q].r=t.data[p].c;
					tb.data[q].c=t.data[p].r;
					tb.data[q].d=t.data[p].d;
					q++;
				}
	}
}

总代码: c++

//稀疏矩阵的三元组表示-算法
#include <stdio.h>
#define M 6
#define N 7
#define MaxSize  100         //矩阵中非零元素最多个数
typedef int ElemType;
typedef struct
{
	int r;					//行号
	int c;					//列号
	ElemType d;				//元素值
} TupNode;					//三元组定义
typedef struct 
{	
	int rows;				//行数
	int cols;				//列数
	int nums;				//非零元素个数
	TupNode data[MaxSize];
} TSMatrix;					//三元组顺序表

void CreatMat(TSMatrix &t,ElemType A[M][N])  //从一个二维稀疏矩阵创建其三元组表示
{
	int i,j;
	t.rows=M;t.cols=N;t.nums=0;
	for (i=0;i<M;i++)
	{
		for (j=0;j<N;j++) 
			if (A[i][j]!=0) 	//只存储非零元素
			{
				t.data[t.nums].r=i;t.data[t.nums].c=j;
				t.data[t.nums].d=A[i][j];t.nums++;
			}
	}
}
bool Value(TSMatrix &t,ElemType x,int i,int j)  //三元组元素赋值
{
	int k=0,k1;
	if (i>=t.rows || j>=t.cols)
		return false;				//失败时返回false
	while (k<t.nums && i>t.data[k].r) k++;					//查找行
	while (k<t.nums && i==t.data[k].r && j>t.data[k].c) k++;//查找列
	if (t.data[k].r==i && t.data[k].c==j)	//存在这样的元素
		t.data[k].d=x;
	else									//不存在这样的元素时插入一个元素
	{	
		for (k1=t.nums-1;k1>=k;k1--)
		{
			t.data[k1+1].r=t.data[k1].r;
			t.data[k1+1].c=t.data[k1].c;
			t.data[k1+1].d=t.data[k1].d;
		}
		t.data[k].r=i;t.data[k].c=j;t.data[k].d=x;
		t.nums++;
	}
	return true;						//成功时返回true
}

bool Assign(TSMatrix t,ElemType &x,int i,int j)  //将指定位置的元素值赋给变量
{
	int k=0;
	if (i>=t.rows || j>=t.cols)
		return false;			//失败时返回false
	while (k<t.nums && i>t.data[k].r) k++;					//查找行
	while (k<t.nums && i==t.data[k].r && j>t.data[k].c) k++;//查找列
	if (t.data[k].r==i && t.data[k].c==j)
		x=t.data[k].d;
	else
		x=0;				//在三元组中没有找到表示是零元素
	return true;			//成功时返回true
}
void DispMat(TSMatrix t)		//输出三元组
{
	int i;
	if (t.nums<=0)			//没有非零元素时返回
		return;
	printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums);
	printf("\t------------------\n");
	for (i=0;i<t.nums;i++)
		printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d);
}
void TranTat(TSMatrix t,TSMatrix &tb)		//矩阵转置
{
	int p,q=0,v;					//q为tb.data的下标
	tb.rows=t.cols;tb.cols=t.rows;tb.nums=t.nums;
	if (t.nums!=0)					//当存在非零元素时执行转置
	{
		for (v=0;v<t.cols;v++)		//tb.data[q]中的记录以c域的次序排列
			for (p=0;p<t.nums;p++)	//p为t.data的下标
				if (t.data[p].c==v)
				{
					tb.data[q].r=t.data[p].c;
					tb.data[q].c=t.data[p].r;
					tb.data[q].d=t.data[p].d;
					q++;
				}
	}
}
int main()
{
	TSMatrix t,tb;
	int x,y=10;
	int A[6][7]={
		{0,0,1,0,0,0,0},
		{0,2,0,0,0,0,0},
		{3,0,0,0,0,0,0},
		{0,0,0,5,0,0,0},
		{0,0,0,0,6,0,0},
		{0,0,0,0,0,7,4}};
	CreatMat(t,A);
	//printf("b:\n"); DispMat(t);
	//if (Assign(t,x,2,5)==true)  //调用时返回true
	//	printf("Assign(t,x,2,5)=>x=%d\n",x);
	//else  //调用时返回false
	//	printf("Assign(t,x,2,5)=>参数错误\n");
	//Value(t,y,2,5);
	//printf("执行Value(t,10,2,5)\n");
	//if (Assign(t,x,2,5)==true)  //调用时返回true
	//	printf("Assign(t,x,2,5)=>x=%d\n",x);
	//else  //调用时返回false
	//	printf("Assign(t,x,2,5)=>参数错误\n");
	//printf("b:\n"); DispMat(t);
	TranTat(t,tb);
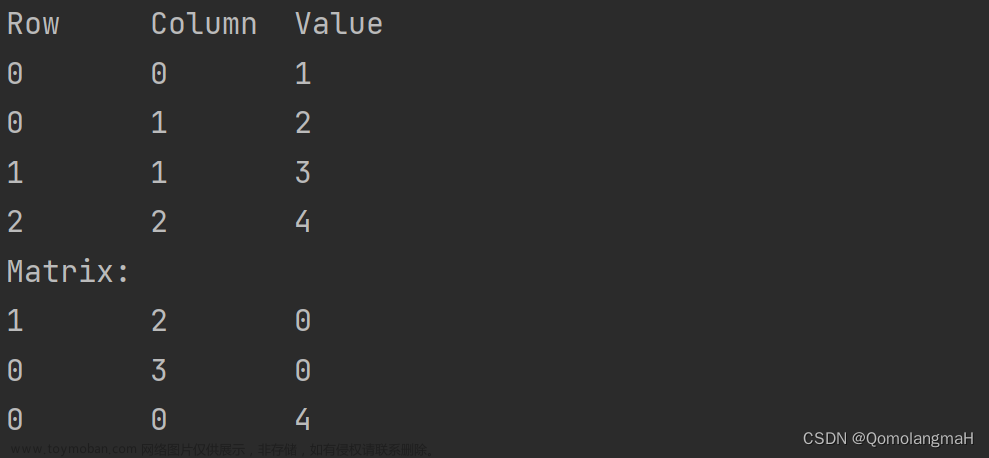
	printf("tb:\n"); DispMat(tb);
	return 1;
}

c总代码（需要自取）

#define  _CRT_SECURE_NO_WARNINGS 1
#include <stdbool.h>
#include <stdio.h>
#include <string.h> 
#include <stdlib.h>
//三元组表示
typedef int ElemType;
#define MaxSize 100
#define M 6
#define N 7
typedef struct Tup
{
	int r;
	int c;
	ElemType d;
}TupNode;
typedef struct TS
{
	int rows;
	int cols;
	int nums;
	TupNode data[MaxSize];
}TsMatrix;
void CreateMat(TsMatrix* t, ElemType A[M][N])
{
	int i, j;
	t->rows = M; t->cols = N; t->nums = 0;
	for(i = 0;i<M;i++)
		for(j=0;j<N;j++)
			if (A[i][j] != 0)
			{
				t->data[t->nums].r = i; t->data[t->nums].c = j; t->data[t->nums].d = A[i][j]; t->nums++;
			}
}
bool Value(TsMatrix* t, ElemType x, int i, int j)
{
	if (i >= t->rows || j >= t->cols) return false;
	int k = 0;
	while (k<t->rows && i>t->data[k].r) k++;
	while (k<t->cols && i == t->data[k].r && j>t->data[k].c) k++;
	if (i == t->data[k].r && j == t->data[k].c) t->data[k].d = x;
	else {
		for (int k1 = t->nums - 1; k1 >= k; k1--)
		{
			t->data[k1 + 1].r = t->data[k1].r;
			t->data[k1 + 1].c = t->data[k1].c;
			t->data[k1 + 1].d = t->data[k1].d;
		}
		t->data[k].r = i; t->data[k].c = j; t->data[k].d = x;
		t->nums++;
	}
	return true;
}
void DispMat(TsMatrix* t)
{
	if (t->nums <= 0) return;
	printf("\t%d\t%d\t%d\n", t->rows, t->cols, t->nums);
	printf("\t--------------------------\n");
	for (int k = 0; k < t->nums; k++)
		printf("\t%d\t%d\t%d\n", t->data[k].r, t->data[k].c, t->data[k].d);
}
bool Assign(TsMatrix* t, ElemType* x, int i, int j)
{
	if (i >= t->rows || j >= t->cols) return false;
	int k = 0;
	while (k < t->nums && i>t->data[k].r) k++;
	while (k<t->nums && i == t->data[k].r && j>t->data[k].c)k++;
	if (t->data[k].r == i && t->data[k].c == j) *x = t->data[k].d;
	else x = 0;
	return true;
}
void TranTat(TsMatrix* t, TsMatrix* b)
{
	if (t->nums != 0)
	{
		b->rows = t->cols; b->cols = t->rows;
		b->nums = t->nums;
		int k1 = 0;
		for(int v = 0;v<t->cols;v++)
			for (int k = 0; k < t->nums; k++)
			{
				if (t->data[k].c == v)
				{
					b->data[k1].r = t->data[k].c;
					b->data[k1].c = t->data[k].r;
					b->data[k1].d = t->data[k].d;
					k1++;
				}
			}
	}

}

int main()
{
	ElemType A[6][7] = {
		{0,0,1,0,0,0,0},
		{0,2,0,0,0,0,0},
		{3,0,0,0,0,0,0},
		{0,0,0,5,0,0,0},
		{0,0,0,0,6,0,0},
		{0,0,0,0,0,7,4} };
	TsMatrix* t = (TsMatrix*)malloc(sizeof(TsMatrix));
	CreateMat(t, A);
	//Value(t, 7, 0, 4);
	ElemType e = 0;
	TsMatrix* b = (TsMatrix*)malloc(sizeof(TsMatrix));
	TranTat(t, b);
	/*Assign(t, &e, 1, 1);
	printf("%d", e);*/
	DispMat(b);
	return 0;
}

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞和收藏，这可以激励我写出更加优秀的文章。

稀疏矩阵的三元组表示----（算法详解）,数据结构,算法,数据结构,排序算法,稀疏矩阵,三元组文章来源地址https://www.toymoban.com/news/detail-812033.html

到了这里，关于稀疏矩阵的三元组表示----（算法详解）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 数据结构·练习·三元组表法实现稀疏矩阵的转置

    一、问题描述 一个mxn的矩阵A，它的转置矩阵B是一个nxm矩阵，且A[i][j]=B[j][i]，0=i=m-1，0=j=n-1，即A的行是B的列，A的列是B的行。 用三元组表对稀疏矩阵进行压缩存储，再进行时间复杂度O(n)的快速转置，最后输出稀疏矩阵。 其中m=4,n=5 二、算法概述 1、问题分析 1）压缩 2）转置

    2024年02月04日
    浏览(43)
  • 【数据结构】数组和字符串（四）：特殊矩阵的压缩存储：稀疏矩阵——三元组表

    【数据结构】数组和字符串（四）：特殊矩阵的压缩存储：稀疏矩阵——三元组表

    【数据结构】数组和字符串（一）：矩阵的数组表示   矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵，如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储，会出现大量存储空间存放重复信息或零元素的情况，这样会造

    2024年02月05日
    浏览(42)
  • 【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）

    【数据结构】稀疏矩阵的压缩存储（三元组表、十字链表）（C语言）

    稀疏矩阵 是指矩阵中大多数元素为零的矩阵。从直观上讲，当非零元素个数低于总元素的30%时，这样的矩阵为稀疏矩阵。 1.1 三元组表的存储结构 稀疏矩阵的三元组表表示法是指只存储非零元素，同时存储该非零元素在矩阵中所处的行号和列号的位置信息。 为方便处理，将

    2023年04月16日
    浏览(39)
  • [数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）

    [数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置）

    实现效果： 1、编写程序任意 输入 一个稀疏矩阵，用 三元组顺序表 压缩存储 稀疏矩阵 。 2、对稀疏矩阵进行 转置 ， 输出 转置后的矩阵。 对应《数据结构(C语言版）》 第5章 数组与广义表 实验： 1、 掌握下三角矩阵的输入、输出、压缩存储算法； 2、 理解稀疏矩阵的三元

    2024年02月03日
    浏览(42)

  • 数据结构第七周 ：（稀疏矩阵快速转置 + 简单文本编辑器 + 三元组的矩阵加法 + 九宫格数独游戏 + 数组主元素 + 螺旋数字矩阵 + 蛇形矩阵）

    【问题描述】 稀疏矩阵的存储不宜用二维数组存储每个元素，那样的话会浪费很多的存储空间。所以可以使用一个一维数组存储其中的非零元素。这个一维数组的元素类型是一个三元组，由非零元素在该稀疏矩阵中的位置（行号和列号对）以及该元组的值构成。而矩阵转置就

    2023年04月21日
    浏览(40)
  • 【数据结构与算法】 完成用十字链表存储的稀疏矩阵的加法运算

    【数据结构与算法】 完成用十字链表存储的稀疏矩阵的加法运算

       Qestion:   完成用十字链表存储的稀疏矩阵的加法运算。 获取两个稀疏矩阵总有多少个非零元素，记作 cnt 。 当 cnt 不为零时一直循环，每循环一次 i++ ，也就是行循环，每循环一次就转移至下一行。 先从第一行开始循环，使得两个工作指针 p 、 q 分别指向两个稀疏矩阵

    2024年02月13日
    浏览(43)
  • 稀疏矩阵的加法和乘法（三元组）

    稀疏矩阵的加法和乘法（三元组）

    三元组方法： 主要的特点就是最后的结果矩阵均由三元组的形式来表达，调用函数再以矩阵形式输出 （1）稀疏矩阵加法 （下图参考懒猫老师《数据结构》课程相关笔记）  这里与普通矩阵加法不同的是，稀疏矩阵的三元组在加法计算时， 如果两个矩阵中的元素相加不为0时

    2024年01月17日
    浏览(45)

  • 三元组操作（相加）——稀疏矩阵（c语言）

     运行环境：TDM-GCC 三元组用来存储 稀疏矩阵 比较节省空间，因为稀疏矩阵大部分都是零元素，而三元组只记录非零元素。 这里两个相加的矩阵有着同样的 i行 j列。 运行结果：         行数：3 列数:4  元素个数：4         --------------------         第0 行  第1 列  1    

    2024年02月05日
    浏览(46)

  • 稀疏矩阵的三元组存储及快速转置

    目录 问题描述  完整代码  详细分析 本节文章 【问题描述】 实现稀疏矩阵的三元组表存储和快速转置运算。 【输入形式】 输入一个整型的6阶稀疏矩阵。 【输出形式】 输出稀疏矩阵的三元组表形式，使用快速转置方法进行转置运算，输出辅助数组num和cpot的值及转置后的三

    2023年04月26日
    浏览(37)
  • 用三元组表实现稀疏矩阵的基本操作

    用三元组表实现稀疏矩阵的基本操作

    目录 问题描述 数据结构 算法设计 算法流程图  源代码  运行结果      ​    编写程序用三元组表实现稀疏矩阵的按列转置操作。 本设计使用三元组表实现。 程序中设计了三个函数： 1.函数InitSPNode()用来建立一个稀疏矩阵的三元组表。     首先输入行数、列数和非零元的

    2024年02月03日
    浏览(37)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包