采用蒙特卡洛模拟法,对家用电动汽车充电负荷进行预测,电动汽车分为快、中、慢三种充电功率,且分为一天一充、一天两充、一天三充三种类型。全部MATLAB代码在下方给出,可以直接运行。
%%%%%%%%%%%%%%%%%%%%%%%%输入电动汽车相关原始数据%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%以下为各种类型电动汽车数量,
%家用电动汽车数量
Nh=958;%输入总数量
a1=0.6;a2=0.3;a3=0.1;%设置一充二充三充比例;
Nh1=Nh*a1;Nh2=Nh*a2;Nh3=Nh*a3;%计算各数
Nh1=round(Nh1);Nh2=round(Nh2);Nh3=round(Nh3);
%%%以下为各种类型电动汽车电池容量,暂设为唯一确定量;从界面输入
Eh=16; %BYD F3DM
%%%以下为各种类型电动汽车快、中、慢充电功率,从界面输入
Pch=3.5; %家用慢充,充电功率,220V*16A=3.5kW
Pcm1=7; %商场、停车场,L-1模式,220V*32A=7kW
Pcm2=12; %商场、停车场,L-2模式,380V*32A=12kW
Pcm3=24; %商场、停车场,L-3模式,380V*63A=24kW
%%%以下为家用电动汽车充电随机分布,期望值需要从界面输入
%一天一充
h1=1140;h2=0.6; %充电起始时刻;%起始荷电状态
%一天二充
h3=540;h4=0.6; %第1次充电起始时刻;%第1次起始荷电状态
h5=1140;h6=0.6; %第2次充电起始时刻;%第2次起始荷电状态
%一天三充
h7=540;h8=0.6; %第1次充电起始时刻;%第1次起始荷电状态
h9=840;h10=0.6; %第2次充电起始时刻;%第2次起始荷电状态
h11=1140;h12=0.6;%第3次充电起始时刻;%第3次起始荷电状态
%%标准差,设为已知;
%一天一充
hh1=120;hh2=0.1;%对应的标准差
%一天二充
hh3=60;hh4=0.1;hh5=120;hh6=0.1;
%一天三充
hh7=60;hh8=0.1;hh9=120;hh10=0.1;hh11=120;hh12=0.1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%蒙特卡洛仿真参数输入%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
M=100;%monte carol 仿真次数
Bh=zeros(M,1440);%创建存放M次仿真的电动汽车充电功率原始矩阵
T=(1:1440);%时间,以分钟为单位,横坐标
r=0; %monte carol仿真循环时,M矩阵每行下移用
%%%%%%%%%%%%%%%%%%%%%开始进行M次蒙特卡洛仿真%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:1:M
Ph=zeros(1,1440);%创建用于存放电动汽车充电功率的一维数组,初始值设为0
r=r+1;
%%%%%%%%以下为家用电动汽车充电功率计算程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%一天一充
for j=1:1:Nh1
Ts=normrnd(h1,hh1); %随机抽取起始充电时刻,h1为均值,hh1为标准差
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h2,hh2); %随机抽取起始充电荷电状态
Tc=(1-Csoc)*Eh*60/(0.9*Pch);%计算充电时长,0.9为充电效率,单位为mins
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
if k>1440
k=k-1440;
Ph(1:k)=Ph(1:k)+Pch;
Ph(Ts:1440)=Ph(Ts:1440)+Pch;
else
Ph(Ts:k)=Ph(Ts:k)+Pch; %充电时段加上充电功率
end
Ph(1:1440)=Ph(1:1440);
end
for t=1:1:1440
Bh(r,t)=Ph(t);%把每次运行Ph的monte carol仿真结果存入B矩阵的行
end
%%一天二充
for j=1:1:Nh2
%第1次充,停车场
Ts=normrnd(h3,hh3); %随机抽取起始充电时刻
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h4,hh4); %随机抽取起始充电荷电状态
%Tc=120; %充电时长限定在2小时
Tc=(1-Csoc)*Eh*60*0.8/(0.9*Pcm1);%计算充电时长,Pcs为单位充电桩
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
Ph(Ts:k)=Ph(Ts:k)+Pcm1; %充电时段加上充电功率
%第2次充,家用
Ts=normrnd(h5,hh5); %随机抽取起始充电时刻
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h6,hh6); %随机抽取起始充电荷电状态
Tc=(1-Csoc)*Eh*60/(0.9*Pch);%计算充电时长,Pcs为单位充电桩
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
if k>=1440
k=k-1440;
Ph(1:k)=Ph(1:k)+Pch;
Ph(Ts:1440)=Ph(Ts:1440)+Pch;
else
Ph(Ts:k)=Ph(Ts:k)+Pch; %充电时段加上充电功率
end
Ph(1:1440)=Ph(1:1440);
end
for t=1:1:1440
Bh(r,t)=Bh(r,t)+Ph(t);%把每次运行Ph的monte carol仿真结果存入B矩阵的行
end
%%一天三充
for j=1:1:Nh3
%第1次充,停车场
Ts=normrnd(h7,hh7); %随机抽取起始充电时刻
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h8,hh8); %随机抽取起始充电荷电状态
%Tc=120; %充电时长限定在2小时
Tc=(1-Csoc)*Eh*60*0.8/(0.9*Pcm1);%计算充电时长,Pcm为单位充电桩
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
Ph(Ts:k)=Ph(Ts:k)+Pcm1; %充电时段加上充电功率
%第2次充,商场
Ts=normrnd(h9,hh9); %随机抽取起始充电时刻
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h10,hh10); %随机抽取起始充电荷电状态
Tc=(1-Csoc)*Eh*60/(0.9*Pcm1);%计算充电时长,Pcs为单位充电桩
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
if k>=1440
k=k-1440;
Ph(1:k)=Ph(1:k)+Pcm1;
Ph(Ts:1440)=Ph(Ts:1440)+Pcm1;
else
Ph(Ts:k)=Ph(Ts:k)+Pcm1; %充电时段加上充电功率
end
%第3次充,回家后
Ts=normrnd(h11,hh11); %随机抽取起始充电时刻
Ts=round(Ts); %对随机抽取的时间取整
Csoc=normrnd(h12,hh12); %随机抽取起始充电荷电状态
Tc=(1-Csoc)*Eh*60/(0.9*Pch);%计算充电时长,Pcs为单位充电桩
Tc=round(Tc); %对充电时长取整
k=Ts+Tc;
if k>=1440
k=k-1440;
Ph(1:k)=Ph(1:k)+Pch;
Ph(Ts:1440)=Ph(Ts:1440)+Pch;
else
Ph(Ts:k)=Ph(Ts:k)+Pch; %充电时段加上充电功率
end
Ph(1:1440)=Ph(1:1440);
end
for t=1:1:1440
Bh(r,t)=Bh(r,t)+Ph(t);%把每次运行Ph的monte carol仿真结果存入B矩阵的行
end
%%%%%%%%以下家用电动汽车充电曲线画图程序部分
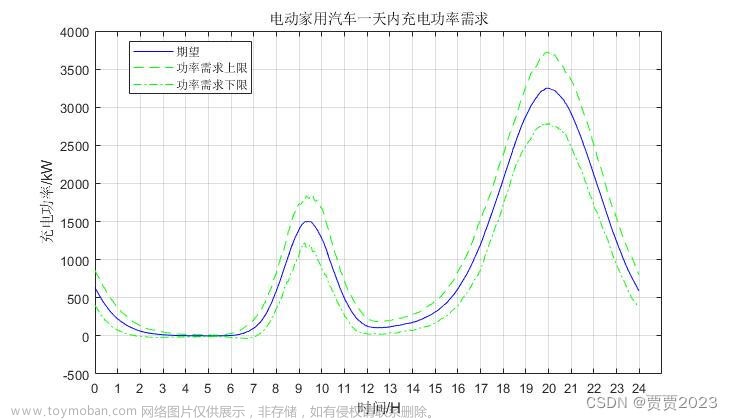
figure(1)
Ph1=mean(Bh,1); %平均充电功率,每一列的平均值
Ph2=std(Bh,0,1); %充电功率的标准差,按列求标准差,且除以N-1
Ph3=Ph1+3*Ph2; %充电功率的概率上线
Ph4=Ph1-3*Ph2; %充电功率的概率下线
plot((T-1)/60,Ph1,'-b',(T-1)/60,Ph3,'--g',(T-1)/60,Ph4,'-.g')
legend('期望','功率需求上限','功率需求下限');
grid
set(gca, 'XTick', [0:1:24])
xlabel('时间/H');
ylabel('充电功率/kW');
title('电动家用汽车一天内充电功率需求');
end
运行结果:文章来源:https://www.toymoban.com/news/detail-812053.html
 文章来源地址https://www.toymoban.com/news/detail-812053.html
文章来源地址https://www.toymoban.com/news/detail-812053.html
到了这里,关于基于蒙特卡洛模拟的家用电动汽车充电负荷预测(MATLAB实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!