一、树是什么?
有根有枝叶便是树!根只有一个,枝叶可以有,也可以没有,可以有一个,也可以有很多。
就像这样:
嗯,应该是这样:

二、一些概念
1、高度
树有多高,嗯,我一米八三!
树的高度怎么算?
高度是啥,就是从下往上到最顶端,从叶节点到根节点。
从每个叶节点开始,一个节点一个节点往上数,数到根节点,最长的那个数就是数的高度。叶节点起始为0.
上面这个树的高度是4。

2、深度
深度,顾名思义,就是从上往下到最低端,从根节点到叶节点。
从根开始,一个节点一个节点往下数,数到每个叶子节点,最长的那个数就是数的深度。根节点的起始为0.
上面这个树的深度是4。

对比上面的高度,看到了哈,数值是一样的,
3、层
一层是什么呢。就是横向的同一高度的所有节点凑一块儿就是一层。
像下面一条线连接了第二层所有的节点:

三、二叉树的遍历
二叉树是什么?
二叉树就是每个节点最多有两个分叉子节点。
遍历是什么意思?
遍历就是一个树的所有节点都点一遍,那么既然要点一遍,总归要遵循一个特定的顺序,不然,乱来的话总会可能漏一个,或者多一个。
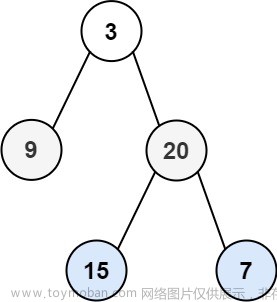
像下面这棵树:

1、前序遍历
顺序:中左右
中 6 -> 左中 5 -> 左 2 -> 右 3 -> 右中 7 -> 右 8
结果就是:6、5、2、3、7、8。
2、中序遍历
顺序:左中右
左 2 -> 中 5 -> 右 3 -> 中 6 -> 右中 7 -> 右 8
结果就是: 2、5、3、6、7、8。
3、后序遍历
顺序:左右中
左 2 -> 右 3 -> 中左 5 -> 右 8 -> 中右 7 -> 中 6
结果就是:2、3、5、8、7、6.
这个顺序,其实很容易混乱。想要记得牢,只需要一点:
【前、中、后】,前为左,右为后,哪个顺序遍历,那么哪个节点就会顺序居中,其它的节点,靠左的居前。
节点的巡查是从根节点出发,从上到下,从左至右巡查,每个节点及其子点巡查完毕后,再跳出到其它节点。
4、附加:层序遍历
层序遍历很简单就是从上到下,一层一层的收拢节点。
第一层 6 -> 第二层 5、7 -> 第三层 2、3、8
结果就是:6、5、7、2、3、8.
四、树能干什么?
树能盖房子!
没错,树通常用来搭建存储数据的房子。
数据存储是对数据的持久化保存,针对数据的操作包括读和写。不过,无论是读还是写,都离不开对数据的检索操作。
1、B树
之前文章介绍过B树及在数据库存储方面的应用:
你好,我是B树
MySQL InnoDB 是怎么使用 B+ 树存数据的?
B 树,即balance tree。其结构及节点数据分布遵循特定的规则。
B 树的算法运行时间通常由它所执行的【磁盘读写操作次数】决定,所有一般会一次尽可能的读写更多的信息。一个B树节点通常和一个完整的磁盘页大小相同,所以磁盘页的大小限制了一个B树节点所能包含孩子节点的个数。
B 树每个节点会包含多少个分支,称之为分支因子。分支因子越大,B 的高度越低,查找关键字所需的磁盘存取次数越少,查询时间越短。这也是为什么会推崇使用B树结构来作为数据底层存储。
2、二叉搜索树
二叉搜索树是以一棵二叉树来组织数据存储,每个节点除了包含数据本身外,还包括指向左节点、右节点及父节点的指针,即key、left、right、p。其中存储数据需满足左中右非降序存储,即left.key <= key <= right.key。
左中右,是不是很熟悉,就是我们上面讲到过的【中序遍历】顺序。【中序遍历】输出的话,整个数列会是非降序排序数列。
搜索树结构通常支持包括查找,最大值,最小值,插入,删除等操作。嗯,这些操作是不是又很熟悉,总之就是一个【日常操作】。
二叉搜索树上的操作时间和它的高度成正比,对于n节点二叉树,通常最坏运行时间为O(lgn)(为什么是O(lgn)呢?这个需要推导,先记住就行了),这个就是树元素随机分步的情况下的结果。极端情况下,一条链从根到叶的话,时间固定就是O(n)了。就像下面这个棵树:

3、红黑树
红黑树也是一个二叉搜索树。那为什么会需要这么一棵树呢?
就是为了避免上面哪种极端或者接近极端情况的出现。它可以【保证最坏的情况下操作时间复杂度为O(lgn)】。
对的,是保证!那怎么保证呢?当然是通过维持红黑树本身的结构特点来实现。
我们上面及到过二叉搜索树节点包含的数据,红黑树会在其基础上增加一个存储位来表示节点的颜色(红或者黑)。通过【对任何一条从根到叶子节点的简单路径上的各个节点颜色进行约束】来确保【没有一路径会比其它路径长2倍】。
红黑树的特点:
-
a)【节点要么红,要么黑】
-
b)【根节点是黑的】
-
c)【叶节点是黑的】
-
d)【如果一个节点是红色的,那么它的子节点是黑色的】
-
e)【对任何一个节点,从该节点到其所有后代叶节点的简单路径上的黑节点数据是相同的】
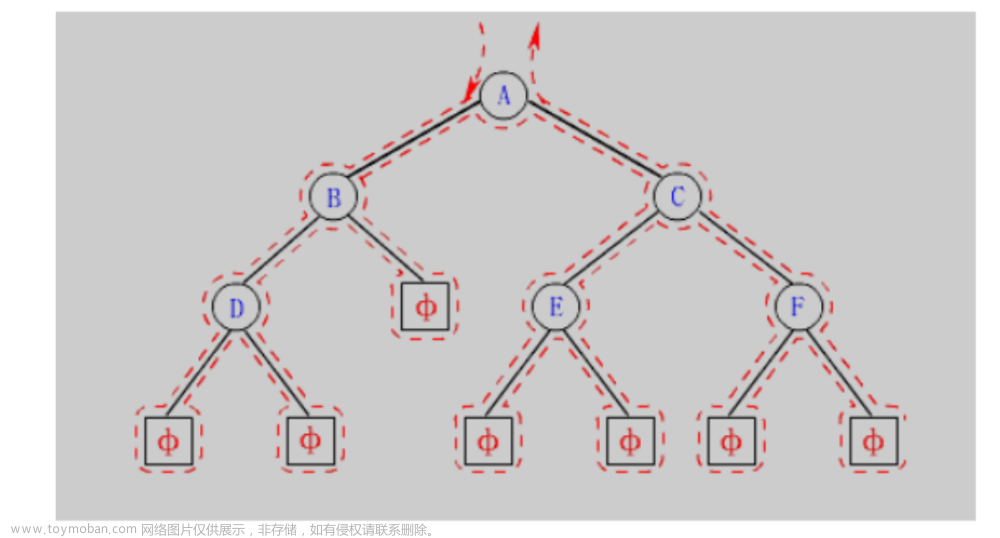
这里有个点需要强调一下,红黑树里所说的叶子节点指的是【外部节点】,也就是不包含 key 的节点。
黑高:从某个节点到达其叶节点的【任何一个(参考e】简单路径上的黑色节点个数称之为黑高。红黑树的黑高即为其根节点的黑高。
一颗有 n 个内部节点的红黑树的高度至多为 2lg(n+1),也即我们前面说的能够保证最坏的情况下操作时间复杂度为O(lgn)。
红黑树有哪些应用呢?文章来源:https://www.toymoban.com/news/detail-812756.html
最常见的就是 HashMap了,用于解决存储元素哈希冲突,当链表元素个数超过8时,即转为红黑树。文章来源地址https://www.toymoban.com/news/detail-812756.html
到了这里,关于数据结构中的一棵树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!