算法回忆录——DFS与BFS-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法回忆录——DFS与BFS。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 广度优先搜索

拿迷宫（二维，上下左右四个方向，入口在左方）来举例，一开始从入口出发，一直往右走，如果遇到了路口，就记录下该路口有几条路可以走，然后选择一条走下去，如果走下去又遇到了一个路口，那么又记录下这个路口有几条路口可以走，然后返回第一个路口，选择未走过的路走下去…

总结一下就是，遇到第一个路口，记录一下该路口有几条路，随便选一条，当遇到第二个路口的时候，又记录一下该路口有几条路，然后返回第一个路口，走另外一条路。也就是说，必须先走完第一个路口的所有路，才能走下一个路口的所有路。

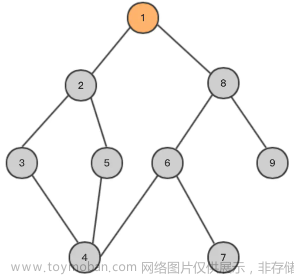
到这，会发现这个过程跟由树的结构很容易解释（圆表示路口，线表示路）：
算法回忆录——DFS与BFS,算法储备,算法,深度优先,宽度优先,python

1表示第一个路口，记录这个路口连通的三个路口，选择从左到右第一条路走
走到2（第二个路口），记录第二个路口连通的两个路口（只记录不走），返回第一个路口，走第二条路
走到3（第三个路口，若有连通的路口就记录，没有就不记录），返回第一个路口，走第三条路
走到4（第四个路口），记录第四个路口连通的一个路口，返回第一个路口
第一个路口所有路走完，按记录的先后顺序来到第二个路口
走到5（第五个路口），记录，返回
走到6，记录，返回。
第二个路口走完，按记录的先后顺序来到第三个路口
第三个路口没有路，来到第四个路口
走到7，记录，返回，
第四个路口走完
来到第五个路口…

而搜索算法针对到是图这类结构，它与树不同的是，拿迷宫来说，树结构的话每条路都是能走到尽头的，图结构的话可能你走到第五个路口，继续走，还能返回到第一个路口，就是这样。

上面的记录步骤可以看到，是先记录哪个路口就走那个路口，可以用队列来实现（先进先出）

下面举一个岛屿最大面积算法题为例：

给定一个由0和1组成的二维数组grid，0表示海洋，1表示岛屿，求岛屿最大面积就是求多个相邻岛屿的总面积最大。（相邻只包括上下左右相邻，斜方向上的相邻不算）

例如:

# 最大面积为5
[[0,1,1,1],
 [0,0,1,0],
 [0,1,0,0],
 [0,1,1,1],
 [0,0,1,0],]
 
# 最大面积为1 
[[0,0,0,0,1,0,1]]

思路：

同迷宫一样，我们从grid[0,0]开始往右找（第一行完了，就从下一行开始）
找到岛屿后，判定它是不是已经遍历过
如果没有遍历过，就将它标记为已遍历
然后判断它的左右上下有没有连着的岛屿，有就标记
直到连着的所有的岛屿的左右上下都没有连着的岛屿就结束。记录此时连着的岛屿的总面积
然后从grid[0,1]再开始…
找完后就能得到最大的岛屿面积

from collections import deque

grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,1,1,0,1,0,0,0,0,0,0,0,0],
        [0,1,0,0,1,1,0,0,1,0,1,0,0],
        [0,1,0,0,1,1,0,0,1,1,1,0,0],
        [0,0,0,0,0,0,0,0,0,0,1,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,0,0,0,0,0,0,1,1,0,0,0,0]]


def BFS(grid):
    # 用来获取一个网格上下左右的四个节点
    around = [[-1, 0], [1, 0], [0, 1], [0, -1]]

    # 获得网格的高度和宽度
    height = len(grid)
    width = len(grid[0])
    # 初始化辅助数组，该数组大小与grid一样，其中元素全部为False
    visit = []
    for i in range(height):
        w = [False for j in range(width)]
        visit.append(w)
    print(len(visit), len(visit[0]))

    # 记录最大岛屿面积
    max_area = 0

    # 因为是广度优先搜索，所以就从每一行开始
    for i in range(height):
        for j in range(width):
            # 如果该格子是个“岛屿”并且没有被遍历过
            if grid[i][j] == 1 and visit[i][j] == False:
                # 将该岛屿标记为已遍历
                visit[i][j] = True
                # 记录下该岛屿的x、y坐标
                x, y = i, j
                # 记录以当前节点开始的岛屿临时最大面积
                tem_max_area = 0
                # 创建队列
                queue = deque()
                # 将该岛屿入队
                queue.appendleft([x,y])
                # 当队列为空时，说明没有临近岛屿
                while queue:
                    # 将队头元素出队
                    elem = queue.popleft()
                    # 每一次出队，临时最大面积就加1
                    tem_max_area += 1
                    # 记录下出队元素的x、y坐标
                    x1, y1 = elem[0], elem[1]
                    # 判断出队元素的上下左右四个方位有没有邻近的网格
                    for k in range(len(around)):
                        # 获取邻近岛屿的x、y坐标
                        x2 = x1 + around[k][0]
                        y2 = y1 + around[k][1]
                        # 邻近岛屿的边界条件，即它们的x、y都大于等于0，都在网格内，然后就是判断该网格是个岛屿还是海，是否已经遍历过
                        if 0 <= x2 < height and 0 <= y2 < width and grid[x2][y2] == 1 and visit[x2][y2] == False:
                            # 若上述条件都满足，就将该岛屿标记为已遍历
                            visit[x2][y2] = True
                            # 并将其入队
                            queue.appendleft([x2, y2])
                # 当队列为空的时候，就说明一次相邻岛屿的面积算完了。保留最大的面积
                if tem_max_area > max_area:
                    max_area = tem_max_area
    return max_area

print(BFS(grid))

2. 深度优先搜索

同样拿迷宫来举例，从入口出发，走到第一个路口，记录，选一条路，走到下一个路口，记录，选一条路…直到走到尽头，返回上一个路口，选择另一条路，走到路口，记录…

总的来说就是指着一条路走到底，记录沿途的路口，走到底了就返回最近的一个路口。

举例步骤：

算法回忆录——DFS与BFS,算法储备,算法,深度优先,宽度优先,python

走到1，记录1
走到2，记录2
走到5，没路了，返回2
走到6，没路了，返回2
2的路走完，返回1
走到3，没路了，返回1
走到4，记录4
走到7，没路了，返回4
…

仍然以岛屿最大面积为例，在写代码之前，需要注意我们是对什么进行搜索。

我们不是对给出的网格进行搜索，而是遇到岛屿之后，开始搜索。就像迷宫一样，把一群相邻连着的岛屿看作迷宫，我们肯定是要找到迷宫的入口，才能开始搜索，在网格“海域”部分搜索是无意义的。

递归：

grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,1,1,0,1,0,0,0,0,0,0,0,0],
        [0,1,0,0,1,1,0,0,1,0,1,0,0],
        [0,1,0,0,1,1,0,0,1,1,1,0,0],
        [0,0,0,0,0,0,0,0,0,0,1,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,0,0,0,0,0,0,1,1,0,0,0,0]]


def DFS(grid, visit, x, y):
    # 递归函数的返回量
    area = 0
    
    # 如果该网格的坐标超出边界（前四个条件）或者该网格不是岛屿（最后一个条件），递归就结束
    # 注意，x表示的是高度，相当于纵轴，y表示的宽度，相当于横轴，不要混淆了
    if x >= len(grid) or x < 0 or y >= len(grid[0]) or y < 0 or grid[x][y] == 0:
        return area
    
    # 如果该岛屿已经遍历过了，递归也结束
    if visit[x][y] == True:
        return area
    
    # 走到这一步，网格一定是岛屿，且一定未被遍历过
    visit[x][y] = True
    area += 1
    
    # 一个网格的上下左右四个方位
    around = [[0, 1], [0, -1], [1, 0], [-1, 0]]

    # 按照我们之前的规则，沿着一条路走到底。这也正好符合递归的特性，递归结束就说明走到底了。
    # 这里有四个方位，循环四次。当一次循环结束，就说明上一次循环已经走到尽头了。
    # 不要去想选择一条路了之后遇到路口又要选择一条路，这样在脑海里一直递归一直递归，很容易猪脑过载
    # 遇到递归我们就当它执行一次就结束，em.....再简单一点就是把DFS函数内部调用的DFS看成一个返回值，然后就不去管了。
    for i in range(len(around)):
        area += DFS(grid, visit, x + around[i][0], y + around[i][1])

    return area



  
  
def MaxArea(grid):
    # 获取网格的高度和宽度
    height = len(grid)
    width = len(grid[0])

    # 最大岛屿面积
    max_area = 0

    # 初始化标记数组
    visit = []
    for i in range(height):
        visit.append([False for i in range(width)])

    # 开始循环，找到未曾遍历过的岛屿，然后开始搜索，计算当前的最大岛屿面积
    for i in range(height):
        for j in range(width):
            # 当该网格是岛屿，且未遍历过时，以此岛屿为起点开始搜索
            if grid[i][j] == 1 and visit[i][j] == False:
                tem_max_area = DFS(grid, visit, i, j)
                # 搜索完后，将以此岛屿为起点搜索得到的面积与最大面积比较，保留较大的那个
                if max_area < tem_max_area:
                    max_area = tem_max_area

    return max_area

print(MaxArea(grid))

使用栈：

from collections import deque

grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,1,1,0,1,0,0,0,0,0,0,0,0],
        [0,1,0,0,1,1,0,0,1,0,1,0,0],
        [0,1,0,0,1,1,0,0,1,1,1,0,0],
        [0,0,0,0,0,0,0,0,0,0,1,0,0],
        [0,0,0,0,0,0,0,1,1,1,0,0,0],
        [0,0,0,0,0,0,0,1,1,0,0,0,0]]


def MaxArea(grid):
    # 获取网格的高度和宽度
    height = len(grid)
    width = len(grid[0])

    # 一个网格邻近的四个网格的坐标（相对的）
    around = [[0, 1], [0, -1], [1, 0], [-1, 0]]

    # 最大岛屿面积
    max_area = 0

    # 初始化标记数组
    visit = []
    for i in range(height):
        visit.append([False for i in range(width)])

    # 开始循环，找到未曾遍历过的岛屿，然后开始搜索，计算当前的最大岛屿面积
    for i in range(height):
        for j in range(width):
            # 如果该网格是岛屿且未被遍历，就开始搜索
            if grid[i][j] == 1 and visit[i][j] == False:
                visit[i][j] = True
                # 以当前岛屿为起点进行搜索得到的岛屿最大面积
                tem_max_area = 0
                # 创建一个栈
                stack = deque()
                # 栈中存储的不是每个网格， 而是每个网格的坐标
                stack.append([i, j])
                # 当栈为空时，就表示搜索结束
                while stack:
                    # 将栈顶元素出栈
                    elem = stack.pop()
                    # 岛屿临时最大面积加1
                    tem_max_area += 1
                    # 获取出栈元素的坐标
                    x1, y1 = elem[0], elem[1]
                    # 开始搜索它邻近的岛屿
                    for k in range(len(around)):
                        # 获取岛屿邻近网格的坐标
                        x2, y2 = x1 + around[k][0], y1 + around[k][1]
                        # 若该坐标满足边界条件，且该坐标是岛屿，且未被遍历，就标记，并且入栈
                        if 0 <= x2 < height and 0 <= y2 < width and grid[x2][y2] == 1 and visit[x2][y2] == False:
                            visit[x2][y2] = True
                            stack.append([x2, y2])

                if max_area < tem_max_area:
                    max_area = tem_max_area

    return max_area

print(MaxArea(grid))