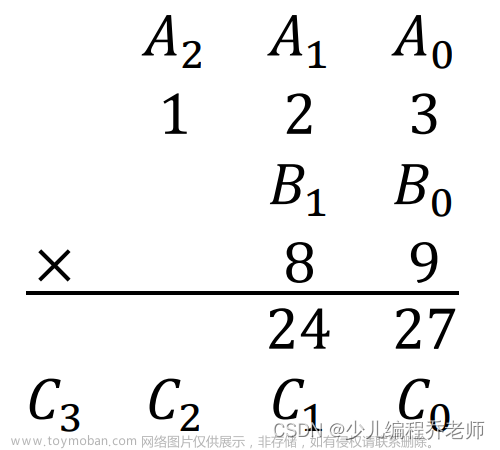目录
加法
减法
乘法
除法
高精度加法的步骤:
1.高精度数字利用字符串读入
2.把字符串翻转存入两个整型数组A、B
3.从低位到高位,逐位求和,进位,存余
4.把数组C从高位到低位依次输出
1.2为准备
vector<int> A, B, C;
string st1,st2;
cin >> st1 >> st2;
int len1 = st1.size(), len2 = st2.size();
for (int i = len1 - 1; ~i ; i--) A.push_back(st1[i] - '0');
for (int i = len2 - 1; ~i ; i--) B.push_back(st2[i] - '0');3为加法具体实现(0按位取反为-1,即-1时结束等价于>=0)
void add(vector<int> A, vector<int> B, vector<int>& C) {
int t = 0, la = A.size(), lb = B.size();
for (int i = 0; i < la || i < lb; i++) {
if (i < la) t += A[i];
if (i < lb) t += B[i];
C.push_back(t % 10); //存余
t /= 10; //进位
}
if (t) C.push_back(t); //最高位
}4为结果输出,翻转输入所以一定也要翻转输出!!!
for (int i = C.size() - 1; ~i; i--) cout << C[i];测试

高精度减法的步骤:
1.高精度数字利用字符串读入
2.把字符串翻转存入两个整型数组A、B
3.若A<B,则交换A,B,输出负号
4.从低位到高位,逐位求差,借位,存差
5.把数组C从高位到低位依次输出
1.2为准备(和加法同理)
vector<int> A, B, C;
string st1,st2;
cin >> st1 >> st2;
int len1 = st1.size(), len2 = st2.size();
for (int i = len1 - 1; ~i ; i--) A.push_back(st1[i] - '0');
for (int i = len2 - 1; ~i ; i--) B.push_back(st2[i] - '0');3 若A<B,则交换A,B,输出负号
if (cmp(A, B)) swap(A, B), cout << '-';若A<B返回true的比较函数cmp()
bool cmp(vector<int> A, vector<int> B) {
if (A.size() != B.size())
return A.size() < B.size();
for (int i = A.size() - 1; ~i; i--)
if (A[i] != B[i])
return A[i] < B[i];
//若A=B,返回false,避免给0加上负号
return false;
}4为减法的具体实现
void sub(vector<int> A, vector<int> B, vector<int>& C) {
int t, la = A.size(), lb = B.size();
for (int i = 0; i < la; i++) {
t = A[i];
if (i < lb)t -= B[i];
if (t < 0) A[i + 1]--, t += 10;//借位
C.push_back(t);//存差
}//C.back()返回最后一个元素,类似C[C.size()-1]
while (C.size() > 1 && !C.back()) C.pop_back();
}//高位连续的0没有意义,需要去掉5为结果输出,翻转输入所以也一定要翻转输出!!!(和加法同理)
for (int i = C.size() - 1; ~i; i--) cout << C[i];测试

高精度乘法的步骤:
1.高精度数字利用字符串读入
2.把字符串翻转存入两个整型数组A、B
3.从低位到高位,累加乘积,进位,存余
4.把数组C从高位到低位依次输出
1.2为准备(和加法、减法同理)
vector<int> A, B, C;
string st1,st2;
cin >> st1 >> st2;
int len1 = st1.size(), len2 = st2.size();
for (int i = len1 - 1; ~i ; i--) A.push_back(st1[i] - '0');
for (int i = len2 - 1; ~i ; i--) B.push_back(st2[i] - '0');3
vector<int> mul(vector<int> A, vector<int> B) {
int la = A.size(), lb = B.size();
vector<int> C(la + lb, 0);
for (int i = 0; i < la; i++) {
for (int j = 0; j < lb; j++) {
C[i + j] += A[i] * B[j];//累加乘积
C[i + j + 1] += C[i + j] / 10;//进位
C[i + j] %= 10;//存余
}
}//去掉高位无意义的0
while (C.size() > 1 && !C.back()) C.pop_back();
return C;
}4
vector<int> C(mul(A, B));
for (int i = C.size() - 1; ~i; i--) cout << C[i];测试(因为这个数据可以用计算器算。。。)

高精度除法的步骤:
1.高精度数字利用字符串读入
2.把字符串翻转存入整型数组A
3.从高位到低位,当前被除数,存商,求余数
4.把数组C从高位到低位依次输出
1.2为准备,注意只存被除数A
vector<int> A, C;
long long b;
string st1;
cin >> st1 >> b;
int len1 = st1.size();
for (int i = len1 - 1; ~i ; i--) A.push_back(st1[i] - '0');3为除法实现
void div(vector<int> A, long long b, vector<int>& C) {
int la = A.size();
long long t = 0;
for (int i = la - 1; ~i; i--) {
t = t * 10 + A[i];//当前被除数
C.push_back(t / b);//存商
t %= b;//余数
}//翻转C,使无意义的连续0在C尾
reverse(C.begin(), C.end());
while (C.size() > 1 && !C.back()) C.pop_back();
}4
for (int i = C.size() - 1; ~i; i--) cout << C[i];测试

这实际是高精度除低精度。
真正的高精度除高精度:
1.高精度数字用字符串读入
2.从高位到低位,逐位“试商”,存商,更新当前被除数
3.翻转输出商
1
string st1, st2, st;
vector<int> C;
cin >> st1 >> st2;2
string sub(string s, string st2) {
vector<int> A, B, C;
for (int i = s.size() - 1; ~i; i--) A.push_back(s[i] - '0');
for (int i = st2.size() - 1; ~i; i--) B.push_back(st2[i] - '0');
int t, la = A.size(), lb = B.size();
for (int i = 0; i < la; i++) {
t = A[i];
if (i < lb) t -= B[i];
if (t < 0) t += 10, A[i + 1]--;
C.push_back(t % 10);
}
string str;
while (C.size() > 1 && !C.back()) C.pop_back();
for (int i = C.size() - 1; ~i; i--) str += C[i] + '0';
return str;
}
bool cmp(string s, string st2) {
if (s.size() != st2.size())
return s.size() > st2.size();
for (int i = 0; i < s.size(); i++) {
if (s[i] != st2[i])
return s[i] > st2[i];
}
return true;
}
string div(string st1, string st2, vector<int>& C) {
string s;
for (int i = 0; i < st1.size(); i++) {
s += st1[i];//s>st2 -> true
int cnt = 0;
while (cmp(s, st2) && cnt < 10) {
s = sub(s, st2);
cnt++;
}
C.push_back(cnt);
}
reverse(C.begin(), C.end());
while (C.size() > 1 && !C.back()) C.pop_back();
return s;
}3文章来源:https://www.toymoban.com/news/detail-812994.html
st = div(st1, st2, C);
for (int i = C.size() - 1; ~i; i--) cout << C[i];
cout << '\n' << st;顺便算了余数文章来源地址https://www.toymoban.com/news/detail-812994.html
到了这里,关于高精度算法笔记·····························的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!