时间复杂度
概念
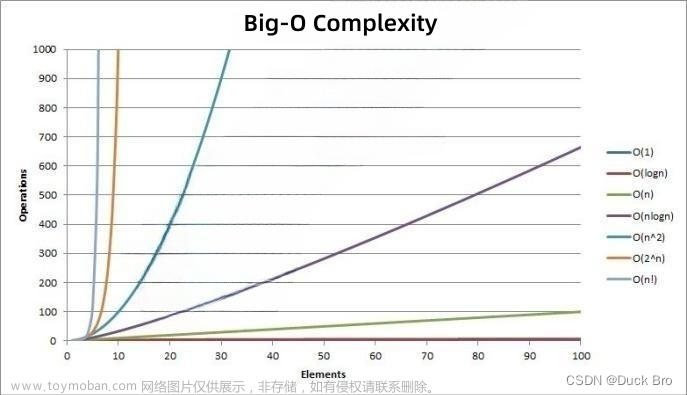
时间复杂度是用来衡量算法执行时间的一个指标。它表示随着输入规模的增加,算法执行时间的增长率。时间复杂度通常用大O符号表示。
在计算时间复杂度时,通常会忽略常数项、低阶项和系数项,只关注随着输入规模增长而导致的主要影响。这是因为在实际应用中,常数项、低阶项和系数项的影响往往可以忽略不计。
常见的时间复杂度有以下几种:
常数时间复杂度(O(1)):无论输入规模的大小,算法的执行时间都是恒定的。
线性时间复杂度(O(n)):算法的执行时间与输入规模成正比。
对数时间复杂度(O(log n)):算法的执行时间与输入规模的对数成正比。
平方时间复杂度(O(n^2)):算法的执行时间与输入规模的平方成正比。
指数时间复杂度(O(2^n)):算法的执行时间与输入规模的指数成正比。
练习
// 请计算一下Func1基本操作执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}答案:O(N^2)
^是平方的意思,*是乘。
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}答案:O(N)
忽略前面的2。
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}答案:O(N+M)
未知数都可能影响结果,都需要写上去。
如果题目有给条件:N远大于M,则技术O(N)。N和M差不多大,则是O(M)或者O(N)。
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}答案:O(1)
k是常数项,有具体数值。就是O(1)。
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, char character )
{
while(*str != '\0')
{
if(*str == character)
return str;
++str;
}
return NULL;
}答案: O(N)
因为最好情况是1,最坏是N,按最坏情况计算。
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}答案: O(N^2)
冒泡排序:
第一次:N
第二次:N-1
第三次:N-2
第N次:1
实际上,这是一个等差数列,运用数学公式就是(N+1)*N/2。忽略+ /,就是O(N^2)。
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n;
while (begin < end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid;
else
return mid;
}
return -1;
}答案:O(log2N),这里格式不支持,是log2的n次方。
// 计算阶乘递归Factorial的时间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}答案:O(N)
函数调用了N次。

空间复杂度
概念
空间复杂度是指算法在执行过程中所需的额外空间的量度。它衡量的是算法所使用的内存空间的数量和大小,包括程序代码本身所占用的空间、输入数据所占用的空间以及算法执行过程中所使用的辅助空间。
空间复杂度的计算通常是根据算法所使用的额外空间的最大值来进行评估。它可以用大O符号(O)来表示,类似于时间复杂度。
常见的空间复杂度有以下几种:
-
O(1) - 常数空间复杂度: 算法所使用的额外空间是固定的,与输入规模无关。常数空间复杂度的算法通常只使用固定数量的变量或常量大小的数据结构。
-
O(n) - 线性空间复杂度: 算法所使用的额外空间与输入规模成线性关系。例如,使用一个数组来存储输入数据。
-
O(n^2) - 平方空间复杂度: 算法所使用的额外空间与输入规模的平方成正比。例如,使用一个二维数组来存储输入数据。
-
O(log n) - 对数空间复杂度: 算法所使用的额外空间与输入规模的对数成正比。例如,使用递归调用栈所占用的空间。
-
O(nlog n) - 线性对数空间复杂度: 算法所使用的额外空间与输入规模的对数乘以线性关系。例如,使用归并排序等分治算法时所占用的空间。
在进行空间复杂度分析时,通常会忽略常数因子和低阶项,只关注随着输入规模增长而增长的部分。
练习
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}答案:O(1)
时间是累积的,空间是不累积的(用完就丢)。
// 计算Fibonacci的空间复杂度?
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i ] = fibArray[ i - 1] + fibArray [i - 2];
}
return fibArray ;
}答案:O(N)
malloc了一个n+1大小的空间,就是N,如果是常数,就是O(1)。
// 计算阶乘递归Factorial的空间复杂度?
long long Factorial(size_t N)
{
return N < 2 ? N : Factorial(N-1)*N;
}答案:O(N),文章来源:https://www.toymoban.com/news/detail-813022.html
最多的时候,开辟了N个栈帧。文章来源地址https://www.toymoban.com/news/detail-813022.html
到了这里,关于c语言版:数据结构(时间复杂度,空间复杂度,练习)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!