力扣_数组29—根据前序与中序遍历序列构建二叉树、根据中序与后序遍历序列构建二叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了力扣_数组29—根据前序与中序遍历序列构建二叉树、根据中序与后序遍历序列构建二叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

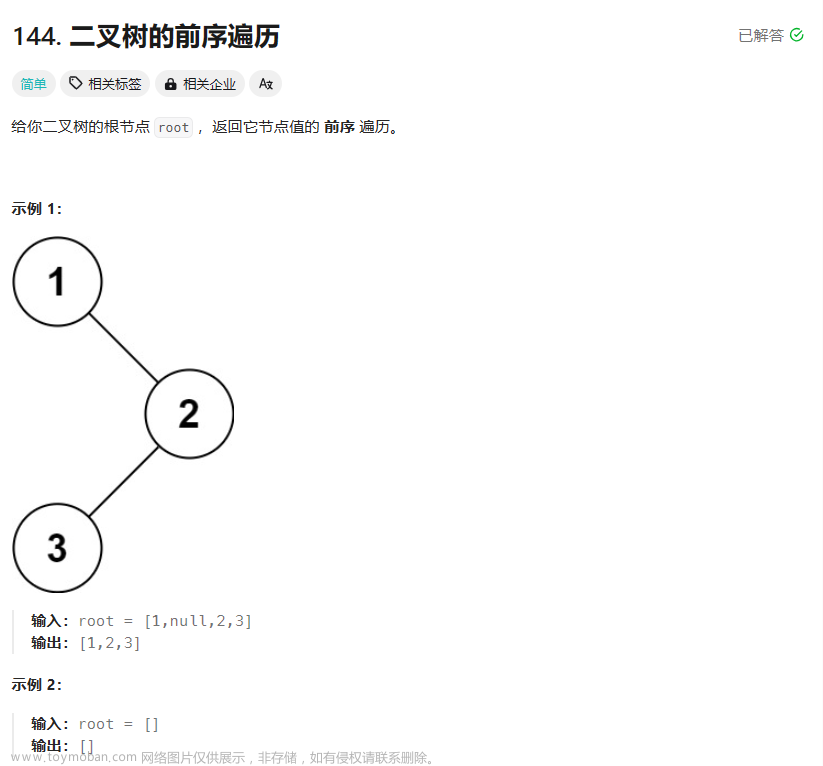
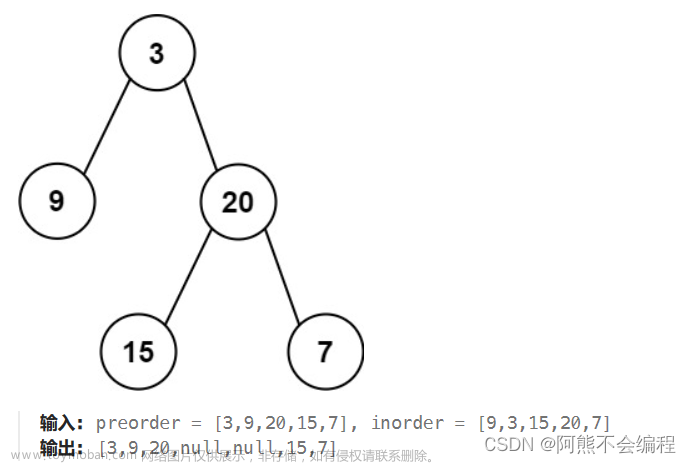
给定两个整数数组 $p reor d er$ 和 $in or d er$ ，其中 $p reor d er$ 是二叉树的先序遍历， $in or d er$ 是同一棵树的中序遍历，请构造二叉树并返回其根节点。文章来源地址https://www.toymoban.com/news/detail-813712.html

复习

前序遍历（先根遍历）：遍历顺序为，根节点—左节点（左子树）—右节点（右子树）
中序遍历（中根遍历）：遍历顺序为，左节点（左子树）—根节点—右节点（右子树）
后序遍历（后根遍历）：遍历顺序为，左节点（左子树）—右节点（右子树）—根节点

思路—递归

对于任意一颗树而言，前序遍历的形式总是
[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
- 也就是说对于前序遍历序列，第一个必是根节点；第二个区间必是左子树的前序遍历序列；第三个区间必是右子树的前序遍历序列；
- 问题是如何确定两个区间的起止点（靠中序遍历序列）
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是
[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
- 根据前序遍历序列找到根节点的位置，根节点前面的部分为左子树的中序遍历序列；后面的部分为右子树的中序遍历序列
- 根据两个中序遍历序列的长度确定前序遍历序列中两个区间的起始点
对于每个子树的前序遍历与中序遍历序列进行同样的操作

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* subTree(vector<int>& preorder, vector<int>& inorder, int pre_l, int pre_r, int in_l, int in_r){
        if(pre_l == pre_r){
            return  new TreeNode(preorder[pre_l]);
        }
        int root_val = preorder[pre_l];
        TreeNode* root = new TreeNode(root_val);
        int tree_l_len = 0;
        for(int i = in_l; i <= in_r; i++){
            if(inorder[i] != root_val){
                tree_l_len++;
            }
            else{
                break;
            }
        }
        int tree_r_len = pre_r-pre_l-tree_l_len;
        if(tree_l_len>0){
            root->left = subTree(preorder, inorder, pre_l+1, pre_l+tree_l_len, in_l, in_l+tree_l_len-1);
        }
        if(tree_r_len>0){
            root->right = subTree(preorder, inorder, pre_l+tree_l_len+1, pre_r, in_r-tree_r_len+1, in_r);
        }
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        TreeNode* ret = subTree(preorder, inorder, 0, preorder.size()-1, 0, preorder.size()-1);
        return ret;
    }

};