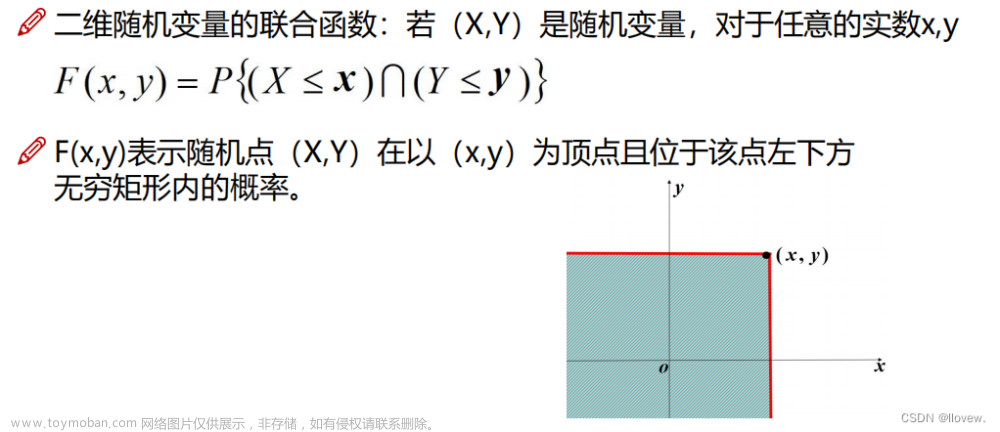
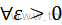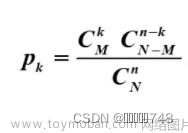概率论中的矩是一种用于描述随机变量分布特征的统计量。矩提供了关于随机变量的各种特征,例如均值、方差、偏度和峰度等。它们对于理解数据的分布以及进行概率分析和推断非常重要。
矩的实际含义可以从数学角度进行解释。对于一个随机变量X,其概率密度函数为f(x),则X的r阶矩定义为:
μ_r = E[X^r] = ∫x^r f(x) dx
其中,E[·]表示期望运算符,x^r表示x的r次方。这意味着r阶矩是随机变量X的r次方的期望。
在实际应用中,矩提供了对数据分布的各种信息。以下是一些常见的矩及其含义:
-
一阶矩(均值):均值是数据分布的中心位置的度量。它表示随机变量的平均值,用于描述数据的集中趋势。
-
二阶矩(方差):方差是数据分布的离散程度的度量。它描述了随机变量与其均值之间的偏离程度,用于衡量数据的分散程度。
-
三阶矩(偏度):偏度度量了数据分布的不对称性。正偏表示分布右侧的尾部比左侧更长,负偏则相反。
-
四阶矩(峰度):峰度度量了数据分布的尖锐程度。它描述了分布的尾部和顶部相对于高斯分布的陡峭程度。
除了以上提到的矩,还有更高阶的矩,它们提供了更详细的数据状态信息。高阶矩表示数据分布的更高级特征,例如更高阶的离散程度、不对称性和尖锐程度。
在概率论和统计学中,高阶矩的计算可能涉及更复杂的数学操作,但它们可以提供关于数据分布的更细粒度的信息。通过计算高阶矩,我们可以进一步了解数据的偏斜、峰度以及其他非常态特征。文章来源:https://www.toymoban.com/news/detail-813920.html
下面是使用Python编程语言计算一阶和二阶矩的示例代码:文章来源地址https://www.toymoban.com/news/detail-813920.html
到了这里,关于概率论中矩的实际含义及高阶矩表示数据的状态的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!