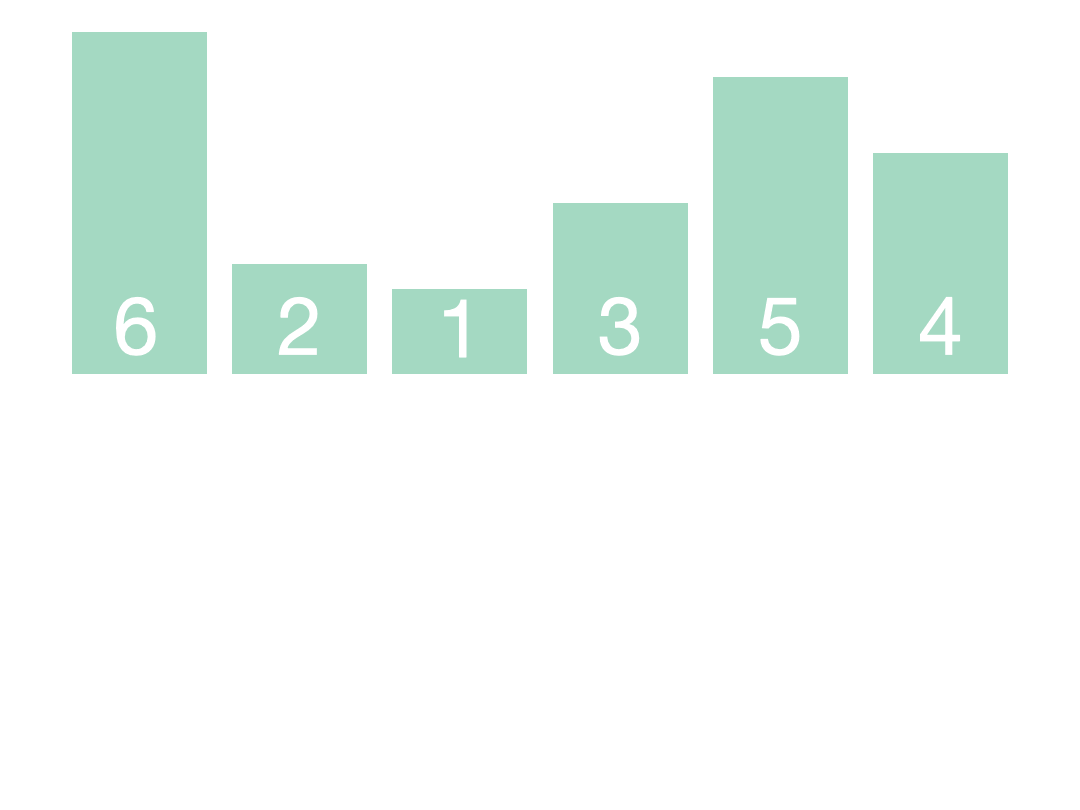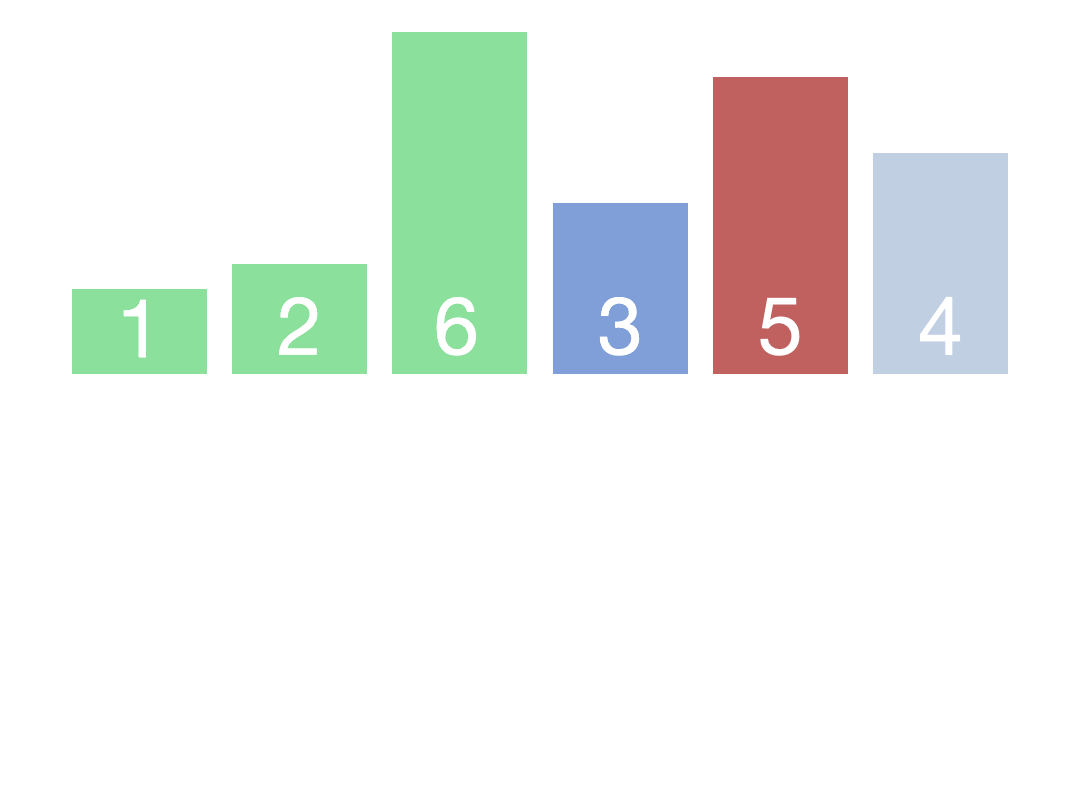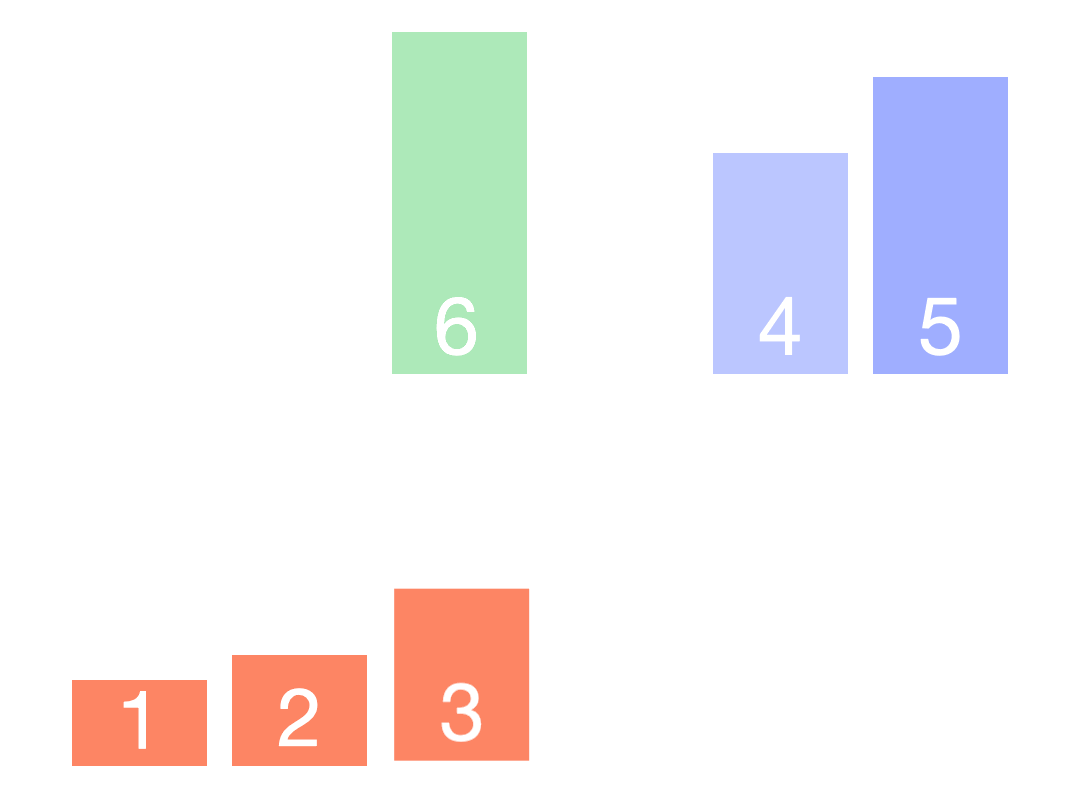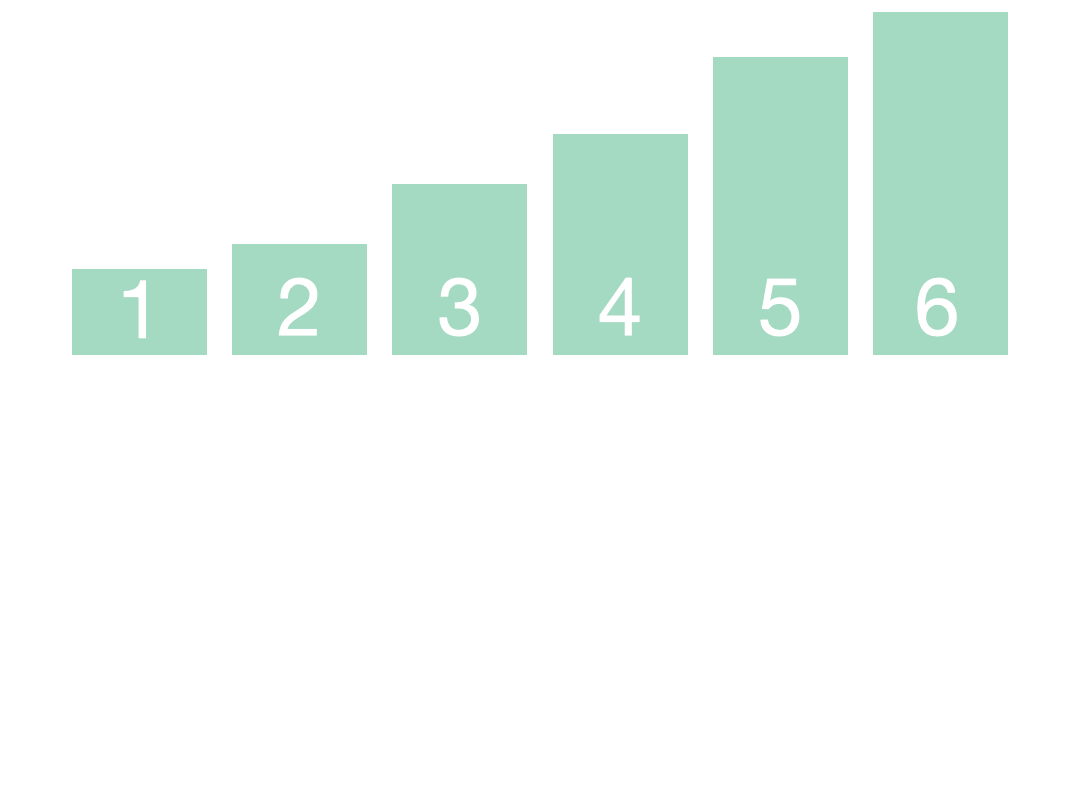一、归并排序
归并排序是一种经典的排序算法,它使用了分治法的思想。下面是归并排序的算法思想:
- 递归地将数组划分成较小的子数组,直到每个子数组的长度为1或者0。
- 将相邻的子数组合并,形成更大的已排序的数组,直到最终得到一个完全排序的数组。
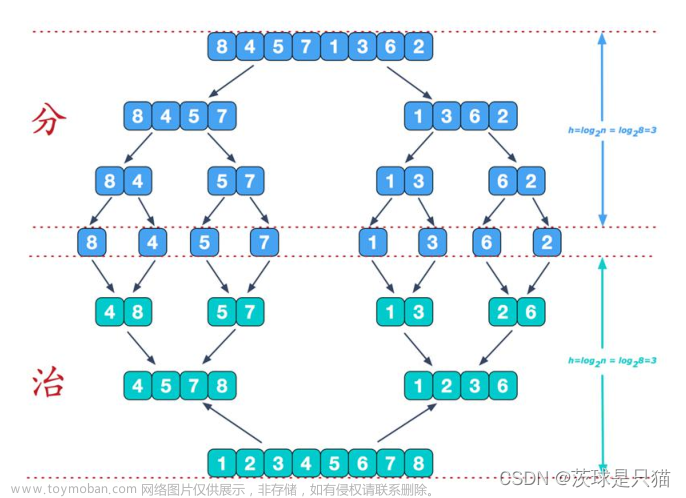
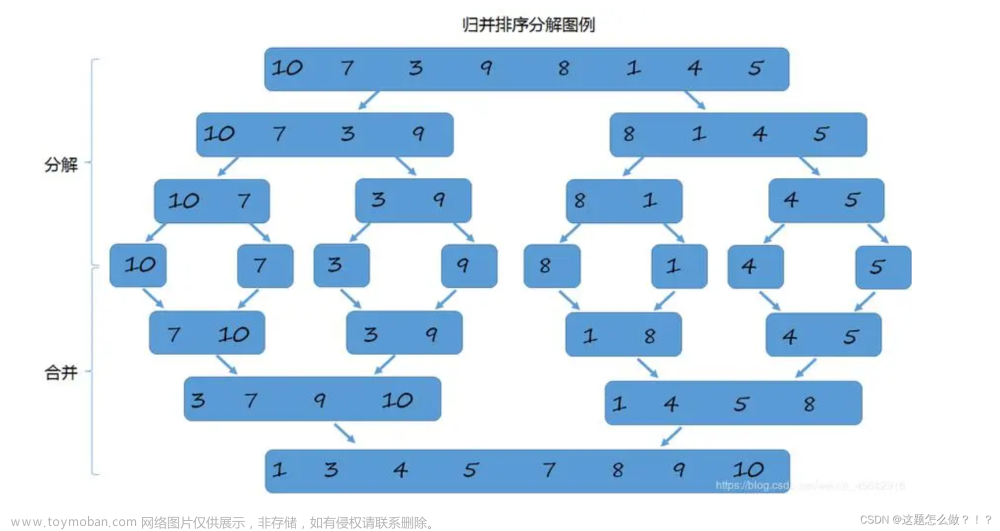
归并排序的过程可以分为三个步骤:拆分(Divide)、合并(Merge)和排序(Sort)。
- 拆分:将待排序的数组不断地划分为两个子数组,直到每个子数组的长度为1或者0。
- 合并:将相邻的子数组合并为一个较大的已排序数组,通过比较两个子数组的首元素,按照从小到大的顺序逐个将元素放入一个辅助数组。
- 排序:重复进行合并的过程,直到最终得到完全排序的数组。
归并排序的时间复杂度为O(nlogn),其中n是待排序数组的长度。空间复杂度为O(n),主要是由于需要使用一个大小与原始数组相同的辅助数组来存储合并的结果。
归并排序是一种稳定的排序算法,即相等元素的相对顺序在排序前后保持不变。在合并的过程中,如果遇到两个相等的元素,我们会先将来自前一个子数组的元素放入辅助数组,这样可以确保相等元素的相对顺序不会改变。

代码实现:
// 归并排序具体功能实现函数
void MergeSortFun(int* a, int* temp, int begin, int end)
{
// 如果数组大小为1或者空,直接返回上一层
if (begin >= end)
{
return;
}
// 划分数组,递归调用 MergeSortFun 对左右子数组进行排序
int mid = (begin + end) / 2;
MergeSortFun(a, temp, begin, mid);
MergeSortFun(a, temp, mid + 1, end);
// 合并两个有序子数组
int begin1 = begin;
int end1 = mid;
int begin2 = mid + 1;
int end2 = end;
int i = begin;
// 依次比较两个子数组的元素,将较小的元素放入辅助数组 temp 中
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
// 将剩余的元素放入辅助数组 temp 中
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
// 将辅助数组 temp 中的元素拷贝回原数组
for (i = begin; i <= end; i++)
{
a[i] = temp[i];
}
}
// 归并排序入口函数
void MergeSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
// 创建大小为 n 的辅助数组 temp
int* temp = (int*)malloc(sizeof(int) * n);
// 调用 MergeSortFun 对数组 a 进行归并排序
MergeSortFun(a, temp, begin, end);
// 释放辅助数组 temp 的内存空间
free(temp);
}二、归并排序非递归实现
归并排序可以使用非递归的方式实现,其算法思想如下:
- 将待排序的数组划分为多个大小为1的子数组。
- 分别对这些子数组进行两两合并,形成新的有序子数组。
- 不断重复步骤2,直到得到一个有序的数组。
具体的非递归实现过程如下:
- 首先,定义一个大小为n的辅助数组temp用于存储合并后的有序子数组。
- 设置一个变量gap初始值为1,表示每次合并的两个子数组的大小。
- 进行多轮合并,直到gap大于等于n。
- 在每一轮合并中,将数组分为多个大小为gap的子数组,将相邻的两个子数组合并为一个有序子数组。合并时,使用双指针i和j分别指向两个子数组的起始位置,比较两个子数组对应位置上的元素大小,较小的元素放入temp数组中,同时移动指针,直到一个子数组遍历完成。将未遍历完的子数组中剩余的元素直接放入temp数组中。
- 更新gap的值为2倍,继续下一轮合并。
- 最后一轮合并时,gap可能大于n,因此需要额外的判断和处理。
- 将temp数组中的元素拷贝回原数组中。
通过不断调整gap的大小,将待排序数组进行分组和合并操作,直到得到一个完全有序的数组。非递归实现的归并排序避免了递归带来的额外开销,提高了算法的效率。、文章来源:https://www.toymoban.com/news/detail-814473.html
 文章来源地址https://www.toymoban.com/news/detail-814473.html
文章来源地址https://www.toymoban.com/news/detail-814473.html
代码实现:
void mergesortnr(int* a, int* temp, int begin, int mid, int end)
{
// 定义指针和索引
int head1 = begin;
int tail1 = mid;
int head2 = mid + 1;
int tail2 = end;
int i = begin;
// 合并两个有序子数组
// [head1,tail1] 和 [head2,tail2] 归并
while (head1 <= tail1 && head2 <= tail2)
{
// 比较两个子数组对应位置上的元素大小,较小的元素放入temp数组中
if (a[head1] < a[head2])
{
temp[i++] = a[head1++];
}
else
{
temp[i++] = a[head2++];
}
}
// 将第一个子数组中剩余的元素放入temp数组中
while (head1 <= tail1)
{
temp[i++] = a[head1++];
}
// 将第二个子数组中剩余的元素放入temp数组中
while (head2 <= tail2)
{
temp[i++] = a[head2++];
}
// 将temp数组中的元素拷贝回原数组中
memcpy(a + begin, temp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSortNR(int *a, int n)
{
// 创建辅助数组
int* temp = (int*)malloc(sizeof(int) * n);
int gap = 1;
// 不断调整gap的大小,分组合并
for (gap = 1; gap < n; gap *= 2)
{
// 对每一组进行合并
for (int i = 0; i < n - gap; i += 2 * gap)
{
// 计算子数组的起始索引、中间索引和结束索引
int begin = i;、
/*如果i + 2 * gap - 1大于等于数组长度n,说明当前的子数组已经超出了数组的范围,此时将结束索引end赋值为n - 1,即最后一个元素的索引。
如果i + 2 * gap - 1小于数组长度n,说明当前的子数组还在数组的范围内,此时将结束索引end赋值为i + 2 * gap - 1。*/
int end = i + 2 * gap - 1 >= n ? n - 1 : i + 2 * gap - 1;
int mid = i + gap - 1;
// 调用mergesortnr函数合并子数组
mergesortnr(a, temp, begin, mid, end);
}
}
}到了这里,关于【数据结构与算法】归并排序详解:归并排序算法,归并排序非递归实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!